Навигация
Эквивалентные множества. Счетные и несчетные множества. Мощность континуума
20614
знаков
0
таблиц
3
изображения
1. Эквивалентные множества. Счетные и несчетные множества. Мощность континуума
Понятие взаимно однозначного соответствия играет большую роль при перенесении представления о «количестве» элементов множества с конечных множеств на бесконечные. Это необходимо, поскольку мы постоянно имеем дело с бесконечными множествами. Вот некоторые из них. 
множество всех чисел натурального ряда; 
множество всех целых чисел (положительные, отрицательные целые числа и нуль).
О количестве точек множества можно говорить только для конечных множеств, а для бесконечных − нельзя. В этом случае говорят о мощности множества. Таким образом, мощность множества − это понятие, которое обобщает понятие «количество элементов» на случай бесконечных множеств. Если же множество конечно, то термины «мощность множества» и «количество элементов множества» − синонимы.
Множества 
и 
называются эквивалентными или равномощными, если между ними можно установить взаимно однозначное соответствие. Это обозначается так: ~. Свойства: ~; ~
~;~,~
~.
Если и эквивалентны, то говорят, что они имеют одинаковую мощность.
Можно привести важный пример эквивалентности бесконечных множеств.
Утверждение 1: Множество 
(натуральных чисел) и множество 
(рациональных чисел, т.е. всех дробей 
) эквивалентны.
Доказательство: достаточно показать, как присвоить собственный номер каждому рациональному числу. Для этого представим каждое рациональное число в виде несократимой дроби:
Такое представление единственно. Высотой рационального числа 
назовем величину 
. Эта высота сама является натуральным числом, т.е. принимает значения 1,2,3,… и т.д. При фиксированном 
существует не более 
различных несократимых дробей, т.к. тогда знаменатель 
может принимать значения 1,2,…,
, а для данного числитель 
числа 
может принимать не более двух значений: 
. Таким образом, с данной высотой 
число рациональных чисел не более 
.
Будем нумеровать дроби в порядке возрастания ; при фиксированном в порядке возрастания , а при фиксированных и - в порядке возрастания . Тогда получим:
и т.д. Ясно, что каждое рациональное число когда-нибудь получит свой порядковый номер. При этом все номера 1,2,3,… будут использованы и разные рациональные числа получат разные номера. Тем самым построено взаимно однозначное соответствие множеств и .
Всякое множество, эквивалентное множеству натуральных чисел, называется счетным множеством.
Исходя из этого определения, можно упомянуть о некоторых теоремах:
1. Из всякого бесконечного множества можно выделить счетное подмножество.
2. Всякое бесконечное подмножество счетного множества тоже счетно.
3. Сумма конечного числа счетных множеств – тоже счетное множество.
4. Сумма счетного множества счетных множеств – тоже счетное множество.
5. Сумма конечного или счетного множества множеств, каждое из которых конечно или счетно, есть конечное или счетное множество.
6. Множество всех рациональных чисел счетно.
7. Множество 
всех алгебраических полиномов с рациональными коэффициентами счетно.
Утверждение 2. Всякое непустое подмножество счетного множества конечно или счетно.
Доказательство: занумеруем элементы счетного множества и перенумеруем затем элементы подмножества в порядке возрастания этих номеров. Если мы исчерпаем все подмножество на конечном шаге, то оно конечно, иначе - счетно.
Утверждение 3. Сумма конечного или счетного числа счетных множеств счетна.
Доказательство. Проведем нумерацию элементов суммы множеств по схеме:
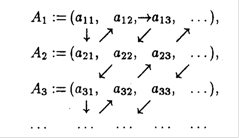
За 
шагов будут заведомо занумерованы все элементы 
.
Стоит обратить внимание, что бесконечные множества, рассмотренные в утверждениях 1-3, оказались равномощными, точнее счетными. Но не все бесконечные множества равномощны. Имеет место следующая теорема.
Теорема 1: совокупность 
всех подмножеств любого множества X сама образует множество, не эквивалентное X. Эта теорема (точнее, ее модификация 
~
) была доказана Г. Кантором (1845-1918) в 1874 г.
Доказательство: (от противного). Пусть 
~
. Значит имеется биективное соответствие 
Тогда, если 
, то ему однозначно соответствует 
. Теперь всякую точку назовем правильной, если она принадлежит своему образу, т.е., если 
. В противном случае эту точку 
будем называть особой точкой. Назовем дефектом множество 
, состоящее из всех особых точек . Тогда ясно, что 
является элементом множества . В силу наличия взаимно однозначного соответствия 
между и найдется такая точка 
. При этом сама точка 
обязана быть либо правильной, либо особой. Но первое не имеет места, поскольку тогда бы по определению правильной точки она принадлежала бы 
, что невозможно, т. к. ко множеству по построению отнесены только особые точки. Но второй случай приводит к противоречию, т. к. тогда по определению особой точки 
, а с другой стороны, тогда точка как особая точка должна войти в дефект по его построению.
Таким образом, предположение о существовании биекции между и во всех случаях ведет к противоречию, т. е. и не эквивалентны.
Следует отметить, что как результат, так и доказательство теоремы справедливы в том случае, когда есть пустое множество. Тогда мощность множества равна 0, а множество состоит ровно из одного элемента, т. е. самого и поэтому мощность равна 
.
Бесконечное множество называется несчетным, если оно не эквивалентно . По теореме 1 несчетным множеством, например, является множество подмножеств , а значит, множество последовательностей, составленных из 0 и 1.
Прием, с помощью которого доказана теорема 1, называется канторов диагональный процесс. Впервые он был применен Кантором в 1874 г. При доказательстве несчетности точек на отрезке. Этот процесс называется диагональным, потому что если в теореме 1 в качестве взять натуральный ряд , то получится, что множество подмножеств, т. е. совокупность последовательностей, составленных из нулей и единиц, не эквивалентно .
Мощность множеств, эквивалентных множеству всех последовательностей, составленных из нулей и единиц, называется мощностью континуума.
Утверждение 4. Множество 
точек отрезка 
имеет мощность континуума.
Доказательство: в двоичной записи каждая точка единичного отрезка может быть записана в виде
Такая запись единственна, за исключением чисел вида 
.А числам такого вида соответствуют в точности две записи (у одной, начиная с некоторого номера, все цифры равны нулю, а у другой – все единицы). Для всех точек, за исключением точек вида 
, установим соответствие так:
А так как множество точек вида счетно, то счетным множеством является также множество последовательностей, им соответствующих. Следовательно, между ними можно установить взаимно однозначное соответствие и тем самым будет установлено взаимно однозначное соответствие между точками отрезка и множеством последовательностей, составленных из нулей и единиц, т. е. множество точек отрезка имеет мощность континуума.
Похожие работы
... о неоклассической производственной функции, то понятию предельной полезности из теории потребления и теории производства соответствует понятие предельной производительности (dY/dXi), которое является здесь одним из ключевых. Законы же убывающей предельной полезности и убывающей предельной нормы замещения, потребительских благ в теории производства сформулировонны как закон убывающей предельной ...
... меньшей и меньшей полезностью,то потребитель станет покупать дополнительные единицы продукта лишь при условии снижения их цены.Потребитель купит, скажем два гамбургера по цене 1$, но вследствие убывающей предельной полезности дополнительных единиц продукта он предпочтет не покупать больш этого продукта по данной цене, т.к., отдавая деньги, он фактически отказывается от других товаров, т.е. ...
... -либо внешнего воздействия, и, наоборот, иногда требуются интенсивные внешние воздействия (катализаторы) для того, чтобы вызвать обратимые переходы изомеров друг в друга. Распространенное в органической химии явление, заключающееся в существовании двух или нескольких изомерных форм молекул, находящихся в состоянии динамического равновесия, называется таутомерией. В настоящее время установлено, ...
... . Пластический шарнир имеет следующие отличия: 1) в нём действует изгибающий момент, равный Mu ; 2) он односторонний; 3) при уменьшении нагрузки он может закрыться. 2. Предельное равновесие балок и рам Приведенное вначале определение предельного состояния системы слишком общее и для достижения результата должно быть конкретизировано. Для балок и рам, материал которых ...
0 комментариев