Навигация
Некоторые интерполяционные свойства семейств конечномерных пространств
4. Некоторые интерполяционные свойства семейств конечномерных пространств
Пусть 1 ≤ p < ∞, 1 ≤ q ≤ ∞. Определим семейство конечномерных пространств:
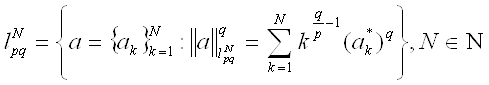
где ![]() невозрастающая перестановка последовательности
невозрастающая перестановка последовательности ![]() . Обозначим через
. Обозначим через ![]() –множество всех непустых подмножеств из {1,2,...N} Пусть M
–множество всех непустых подмножеств из {1,2,...N} Пусть M![]()
![]() , 1 ≤ p < ∞, 1 ≤ q ≤ ∞, множество M назовем сетью.
, 1 ≤ p < ∞, 1 ≤ q ≤ ∞, множество M назовем сетью.
Определим семейство конечномерных пространств
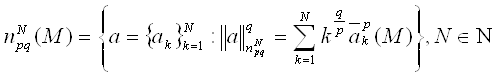
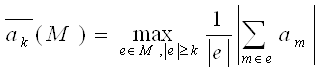
|e| - количество элементов множества e.
При q=∞ положим
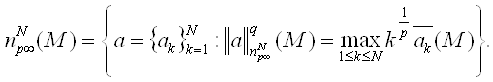
Данные пространства являются конечномерными аналогами сетевых пространств, введенных в [1].
Будем говорить что {AN} ↪ {BN} если существует константа c, такая что ![]() для любого
для любого ![]() , где c не зависит от
, где c не зависит от ![]() .
.
Лемма 4.1 Пусть 1 ≤ q <q1≤ ∞, 1 ≤ p ≤ ∞, ![]() . Тогда имеет место вложение
. Тогда имеет место вложение
![]() ↪
↪ ![]()
то есть
![]()
где с не зависит от выбора N.
Доказательство. Пусть ![]()
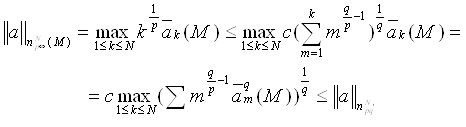 (1)
(1)
то есть ![]() ↪
↪![]()
Теперь рассмотрим случай, когда 1 ≤ q <q1< ∞, и воспользуемся неравенством (1)
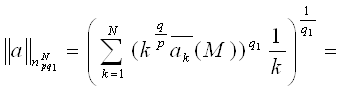
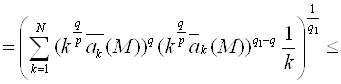
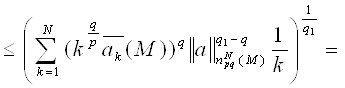
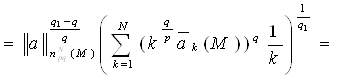
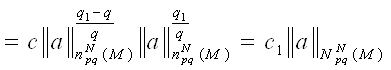
Лемма доказана.
Лемма 4.2 Пусть 1≤p<p1<∞, 1≤q,q1≤∞. Тогда имеем место вложение
![]() ↪
↪ ![]()
Доказательство.
Согласно условию леммы, нам достаточно доказать вложения при p < p1 :
![]() ↪
↪ ![]()
Получаем:
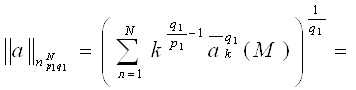
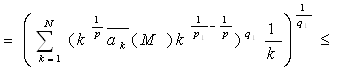
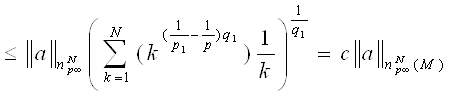
Лемма доказана.
Лемма 4.3 Пусть 1<p<∞, 1≤q≤∞, M= ![]() . Тогда
. Тогда
![]()
![]()
Равенства понимаются с точностью до эквивалентности норм, причем константы не зависят от![]() .
.
Доказательство. Сначала докажем соотношение:
 (2)
(2)
Заметим, что
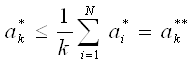
Поэтому
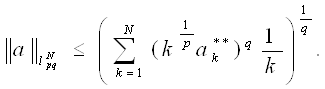
Теперь покажем обратное неравенство. Пусть ![]() . Учитывая выбор
. Учитывая выбор ![]() имеем.
имеем.
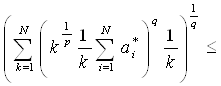

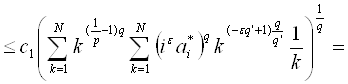
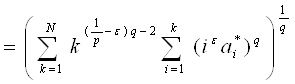 ~
~
~ 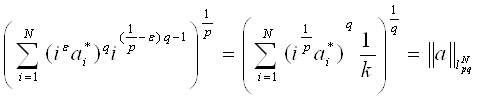
Заметим, что

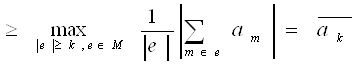
Согласно (2) получаем:
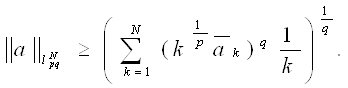
то есть ![]() ↪
↪![]() .
.
Докажем обратное включение. Пусть ![]() Введем следующие обозначения:
Введем следующие обозначения:

Тогда
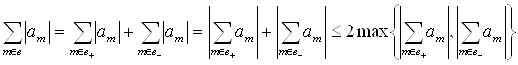 .
.
Пусть для определенности
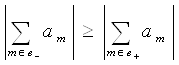 .
.
Возможны следующие случаи:
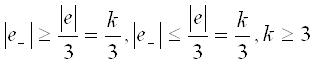 .
.
В первом случае получаем, что
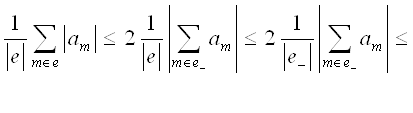
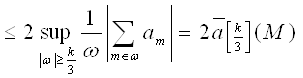 .
.
Во втором случае ![]() , следовательно
, следовательно ![]() . Представим
. Представим ![]() , тогда
, тогда ![]() . Здесь и далее
. Здесь и далее ![]() - целая часть числа
- целая часть числа ![]() .
.
Получаем
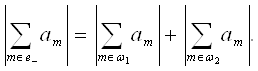
Заметим, что существует ![]() такое, что
такое, что
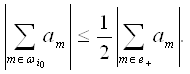
Положим ![]() Тогда
Тогда ![]() .
.

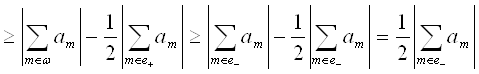 .
.
Таким образом, получаем

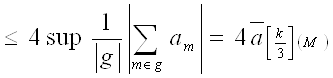
Из того, что

Имеем

То есть ![]() . Следовательно
. Следовательно ![]() ↪
↪ ![]() где соответствующие константы не зависят от N.
где соответствующие константы не зависят от N.
Лемма доказана.
Для пары пространств ![]() определим интерполяционные пространства
определим интерполяционные пространства ![]() аналогично [5] .
аналогично [5] .
Пусть ![]()
![]() , тогда
, тогда

где ![]()
При q=∞
![]()
Лемма 4.4 Пусть ![]()
![]() , d>1. Тогда
, d>1. Тогда
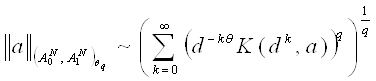
![]()
Справедлива следующая
Теорема 4.1 Пусть ≤p0<p1<∞, 1<q0,q1≤∞, M – произвольная сеть. Тогда
![]() ↪
↪ ![]()
где ![]()
Доказательство.
Учитывая, что ![]() ↪
↪![]() нам достаточно, доказать следующее вложение
нам достаточно, доказать следующее вложение
![]() ↪
↪ ![]()
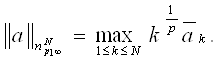
Пусть ![]() Рассмотрим произвольное представление a=a0+a1, где
Рассмотрим произвольное представление a=a0+a1, где
![]() тогда
тогда
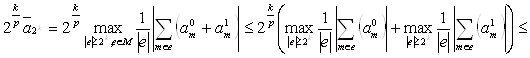

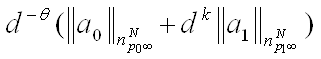 (3)
(3)
Так как представление a=a0+a1 произвольно, то из (3) следует
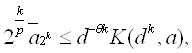
Где ![]() Рассматривая норму элемента в пространстве и применяя
Рассматривая норму элемента в пространстве и применяя
лемму 4.4 , получаем:
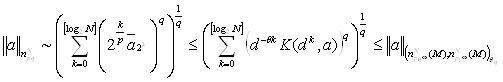
Теорема доказана.
Теорема 4.2 Пусть 1≤p0<p1<∞, 1<q0,q1≤∞, ![]() Тогда имеет место равенство
Тогда имеет место равенство
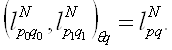
Это равенство понимается в смысле эквивалентности норм с константами, не зависящими ![]() N.
N.
Доказательство. По теореме 4.1 и того, что ![]() является обобщением пространств Лоренца нам достаточно доказать следующее вложение:
является обобщением пространств Лоренца нам достаточно доказать следующее вложение:
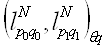 ↩
↩ ![]()
![]() .
.
Определим элементы ![]() и
и ![]() следующим образом
следующим образом
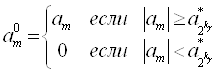
![]() , тогда
, тогда ![]() .
.
Заметим что
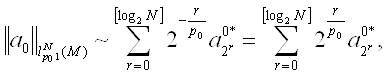 (4)
(4)
где ![]()
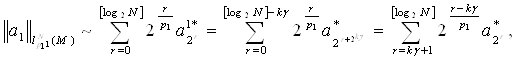 (5)
(5)
где ![]()
Тогда
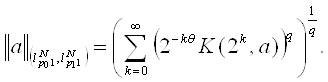
Из (4) и (5) имеем:
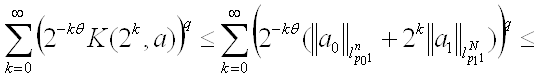
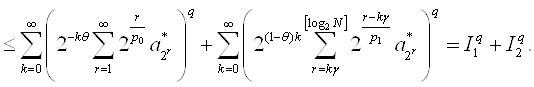
Оценим отдельно каждое из слагаемых последнего равенства, используя неравенство Гельдера:

 ~
~

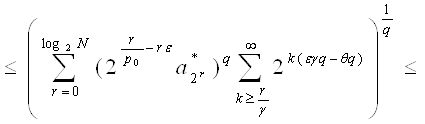
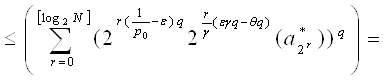

где ![]() .
.
Таким образом, получаем, что ![]() Аналогично рассмотрим второе слагаемое:
Аналогично рассмотрим второе слагаемое:

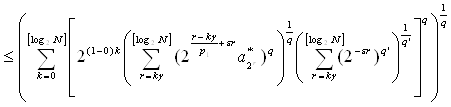 ~
~
~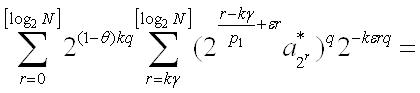
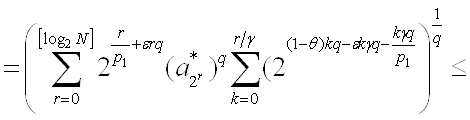
 ~
~ ![]()
Таким образом, получаем
![]()
где c не зависит от ![]() .
.
Теорема доказана.
Теорема 4.3 Пусть ![]() - матрица
- матрица ![]()
![]()
![]() , тогда
, тогда
![]() ~
~ 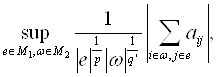
Причем соответствующие константы не зависят от ![]()
Доказательство.
Воспользуемся эквивалентными представлением нормы ![]() и неравенством о перестановках, получим
и неравенством о перестановках, получим
![]() ~
~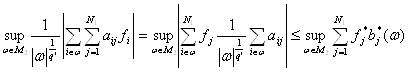
где ![]() - невозрастающая перестановка последовательности
- невозрастающая перестановка последовательности 
Применим неравенство Гельдера

Учитывая лемму 3, имеем
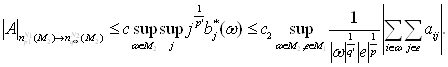
Обратно, пусть e произвольное множество из M1, ![]() , где
, где

Тогда


В силу произвольности выбора e из M1 получаем требуемый результат.
Следствие. Пусть ![]() - матрица
- матрица ![]()
![]()
![]()
p0<p1, q0<q1, ![]() тогда
тогда
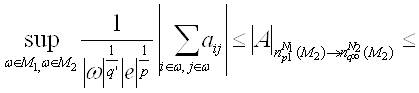
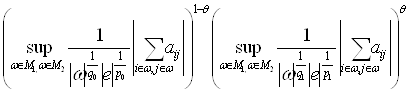
Доказательство. Из теоремы 3 следует, что
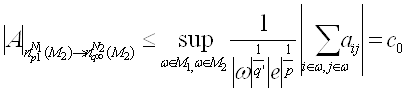
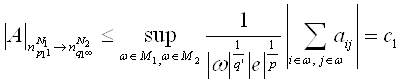
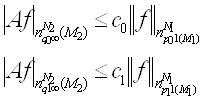
Воспользуемся интерполяционными теоремами 1,2, получаем
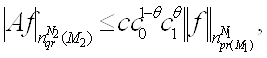
то есть
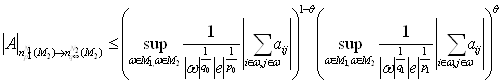
С другой стороны по лемме 1 и теореме 3 имеем

![]() ,
,
Следствие доказано.
Заключение
В данной курсовой работе приведены и доказаны некоторые свойства конечномерных пространств, а именно пространств Лоренца и сетевых пространств.
Полученные результаты могут быть полезны для студентов, магистрантов, аспирантов и преподавателей. Кроме того, данный материал может быть использован для чтения спецкурсов и спецсеминаров.
Список использованной литературы
1. Берг Й., Лефстрем Й. Интерполяционные пространства. Введение. М.: Мир, 1980.
2. Гохберг И.Ц., Крейн М.Г. Введение в теорию линейных несамосопряженных операторов. М.: Наука, 1965.
3. Костюченко А.Г., Нурсултанов Е.Д. Об интегральных операторах в пространствах. Фундаментальная и прикладная математика. Т.5. №2, 1999. С. 475-491.
4. Костюченко А.Г., Нурсултанов Е.Д. Теория управления катастрофами. //Успехи математических наук, 1998. Т.53. Выпуск 2.
5. Нурсултанов Е.Д. Сетевые пространства и неравенства типа Харди-Литтлвуда //Матем.сборник.-1998.-Т.189, №3.-С.83-102.
6. Таджигитов А.А. О зависимости нормы матрицы от взаимного расположения ее элементов. // Материалы Международной научной конференции "Современные проблемы теории функций и их приложения", Саратов, Россия, 2004, с. 177-178.
7. Таджигитов А.А. О норме и спектральном радиусе неотрицательных матриц. //Материалы Международной научно-практической конференции "Современные исследования в астрофизике и физико-математических науках", Петропавловск, 2004, с. 104-107.
8. Таджигитов А.А. Интерполяционные свойства конечномерных пространств. //Международная научная конференция студентов, аспирантов и молодых ученых "Ломоносов 2005", Астана, 2005, с. 41-42.
Похожие работы
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
0 комментариев