Навигация
Незнайка решил несколько примеров на сложение и вычитание десятичных дробей. Найдите ошибки и объясните их
2. Незнайка решил несколько примеров на сложение и вычитание десятичных дробей. Найдите ошибки и объясните их.
2,7+3,651+6,351; 0,325+11,76=15,01; 0,17+1+0,18;
2-0,63=1,63; 117,7-10,07=107,77; 0,632-0,124=0,508.
3. Незнайка решил уравнение х+3,75=6,9 тремя способами, но ответы не совпали. Почему? Найдите ошибки и объясните их.
Способ I. х=6,9-3,75, х=3,25.
Способ II. х=6,9+3,75, х=4,44.
Способ III. х
 |
=6,9-3,75, х=3,15.
4. Перед вами примеры на умножение десятичных дробей. Найдите ошибки.
0,0027·1000=0,27; 4,5·55=247,5; 0,24·1,2=2,88.
5. Проверьте примеры на деление десятичных дробей. Найдите ошибки и объясните их.
1,7:100=0,17; 0,035:7=0,005; 0,521:0,008=651,25.
6. Незнайке задали следующее задание: найти такое значение х, при котором равенство 9:10=9·х было бы верно. Не долго думая, он записал следующий ответ: х=0,01. Прав ли Незнайка? Если нет, то докажите свою точку зрения.
7. Незнайку попросили, не умножая определить, сколько получится цифр в произведении 0,54·21,4·11,8 справа от запятой. Ответ Незнайки – 3 цифры. Прав ли он?
Но не всегда использование игры полностью целесообразно. Это может быть связано, например, с большим количеством времени, которое требуется на проведение всей игры. В этом случае оправдано использование игровых моментов или занимательных задач, которые имеют непривычную форму или необычны в организации выполнения задания. Игровые моменты несут те же функции, что и игры, но требуют меньше времени на подготовку и проведение. Они являются элементами игры, не требующими обучению правилам. К тому же использование игровых моментов и занимательных задач полностью согласуется со вторым принципом – разнообразия видов деятельности; смена вида деятельности – лучший отдых.
Ученики быстро утомляются при выполнении одного и того же вида деятельности. И здесь на помощь приходят игровые моменты и занимательные задачи, которые позволяют прервать монотонное течение урока, сменить род деятельности, отдохнуть с пользой.
В качестве иллюстрации приведем несколько вариантов игровых моментов и занимательных задач.
Игровой момент №1.На столе лежат карточки, на которых написаны следующие числа:
0,25; ![]() ; 0,75;
; 0,75; ![]() ; 1,2;
; 1,2; ![]() ; 0,5;
; 0,5; ![]() ; 0,0011;
; 0,0011; ![]() ;
;
0,975; ![]() ; 1,05;
; 1,05; ![]() ; 0,8;
0,6;
; 0,8;
0,6; ![]() ; 2,5; 1,02.
; 2,5; 1,02.
Учитель вызывает к доске первого ученика и просит его за некоторое время отобрать карточки, на которых написаны десятичные дроби. Второй ученик раскладывает отобранные карточки в порядке возрастания. Третий ученик отбирает из оставшихся карточек те, на которых написаны дроби, которые можно перевести в десятичные дроби. Четвертый участник находит равные им десятичные дроби.
Игровой момент №2.Учитель просит первого ученика назвать любое число в виде десятичной дроби. Второго ученика учитель просит назвать число, меньше того числа, которое заключено между первыми двумя (такое число, которое больше второго, но меньше первого). Задание повторяется несколько раз.
Игровой момент №3. Даны числа: 0,25; 0,75; 0,5; 0,1; 0,05; 0,2; 0,15; 0,6; 0,4. Используя каждое число только один раз, надо составить три верных равенства.
Игровой момент №4. На доске закреплены следующие карточки:
| 1,7 | 2,8 | 1,9 | 3,7 | 4,8 | 3,9 |
| 2,5 | 2,1 | 3,3 | 4,3 | 2,3 | 1,1 |
Учитель вызывает ученика и просит его в течение одной минуты назвать числа в порядке убывания. Следующий ученик должен за одну минуту называть числа в порядке возрастания.
Еще одна форма работы, которая очень нравится ученикам, - это тесты «Проверь себя сам». Цель использования данных тестов: развитие критичности мышления, самоконтроля, внимания. При составлении тестов используется картотека типичных ошибок. Приводим пример теста по теме «Действия с десятичными дробями» (сложение и вычитание).
1. Выполните сложение: 0,17+1
а. 1,17 б. 0,18 в. 0,27
2. Укажите, в каком случае сложение десятичных дробей выполнено правильно: 0,325+11,76
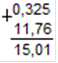
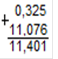
 а. б. в.
а. б. в.
3. Выполните вычитание: 2-0,63
а. 0,61 б. 1,37 в. 1,63
4. Найдите неизвестное число, для которого верно равенство х+3,75=6,9
а. 3,15 б. 10,65 в. 3,25
5.Найдите неизвестное число, для которого верно равенство17,96-у=5,34
а. 12,62 б. 35,44 в. 23,30
6. Найдите неизвестное число, для которого верно равенство 0,1+0,01+х+0,001=1
а. 0,999 б. 0,899 в. 0,889
7. Вычислите: 11,08+0,62-10,09+0,71
а. 2,32 б. 0,9 в. 1,32
8. Собственная скорость лодки равна 3,65 км/ч. Найдите скорость лодки против течения, если скорость течения реки равна 0,8 км/ч.
а. 4,45 км/ч б. 2,85 км/ч в. 3,57 км/ч
9. Скорость катера против течения равна 36,75 км/ч. Найдите скорость лодки по течению, если скорость течения реки равна 5,6 км/ч.
а. 42,35 км/ч б. 47,95 км/ч в. 31,15 км/ч
10. В первый день бригада собрала 4,5 тонн картофеля, во второй день на 0,8 тонн меньше, а в третий день на 2,25 тонн больше, чем во второй. Сколько тонн картофеля собрала бригада за три дня?
а. 14,15 т. б. 9,65 т. в. 10,45 т.
Ответы: 1-а. 2-в. 3-б. 4-а. 5-а. 6-в. 7-а. 8-б. 9-б. 10-а.
Следующим приемом является математический диктант – одна из форм контроля знаний. Первая цель при использовании данного вида работы – проверка уровня готовности учащихся к дальнейшей работе. Каждый учитель знает, как трудно дети воспринимают язык математики на слух У учащихся 5 – 6 классов основным является наглядно-образное мышление. Слышать и слушать учащихся нужно учить. Следовательно, вторая цель: научить детей слышать и понимать язык математики. Надо отметить, что такую работу нужно проводить систематически.
Составление математического диктанта:
1. составляется текст диктанта (с ответами на все задания), дается обоснование содержания;
2. указывается, на какое время рассчитан диктант;
3. описывается методика проведения (слуховой, зрительно-слуховой, зрительный, использование карточек, кодопозитивов, запись на магнитофон, использование переносных досок, индивидуальных досок и т. д.);
4. дается пример выполнения работы учеником.
Для иллюстрации приведем пример математического диктанта по теме «Десятичная запись дробных чисел».
1. Запишите в виде десятичной дроби:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
2. Запишите в виде обыкновенной дроби или смешанного числа: 3,5; 18,04; 0,57; 0,005.
3. Запишите десятичную дробь 1,032. Сколько единиц в разряде сотых этой дроби?
4. Запишите десятичную дробь 135,19. Сколько единиц в разряде единиц этой дроби?
При такой форме работы можно использовать метод «закрытой доски»: доска закрыта; сидящие за партами должны выполнить задание самостоятельно; по окончании работы доска открывается, ученики проверяют свою работу и сами оценивают ее.
Исследовательские работы. Если проанализировать работу детей на уроках, то становится заметной общая тенденция: ученики почти не задают вопросов. Почему? В первую очередь потому, что им просто не интересно. Становится очевидным, что процесс обучения нужно сделать интересным для учеников. Нужно искусственно создать такую ситуацию, при которой ученики вовлекаются в процесс самостоятельного поиска и открытий новых знаний, даже если для этого придется использовать дополнительную литературу. Естественно, что на первом этапе эта работа направляется и контролируется учителем. Только такое обучение ведет к развитию творческих способностей детей и его можно назвать развивающим обучением.
Целью исследовательских работ является освоение системы и пути получения знаний посредством формирования познавательной деятельности ученика и развития его творческих способностей.
При выполнении исследовательских работ дети учатся ставить вопросы и находить на них ответы, сотрудничать с другими учениками, одновременно сохраняя свою индивидуальность, выходить из нестандартных ситуаций и многое другое.
Творческие задания и конкурсы – это написание сказок, задач, сценарием КВН и т. д. Цель этих задании заключается в формировании интереса к математике, развитии творческого мышления.
Далеко не все в учебном материале интересно для учащихся. Важным стимулом познавательного интереса является процесс творчества. При этом в процессе обучения школьник находит привлекательные стороны, сам процесс обучения несет в себе положительный заряд.
Хочется отметить, что выполняя творческие задания, дети проявляют большую изобретательность, пишут многостраничные рефераты, математические фокусы, сценарии сказок и КВНов, математические кроссворды, наглядные пособия и т. д. Примеры таких заданий имеются в учебнике «Математика» 5 класс, публикуются в газете «Математика».
Чем чаще проверяется и оценивается работа школьника, тем интереснее ему работать. Третий принцип можно сформулировать так: любая работа должна быть оценена.
Для этого устраиваются специальные уроки, на которых решаются задачи и разгадываются кроссворды, созданные учениками, организуются конкурсы работ. Дети высказывают свои впечатления, пишут рецензии. Лучшие работы (по мнению детей и учителей) вывешиваются на стенд. [10,6]
Еще одним средством формирования устных вычислительных навыков являются упражнения. Устные упражнения являются одной из важнейших составляющих развивающего обучения. Именно во время устной работы пятиклассник эффективно учится устанавливать связи между объектами, явлениями, сравнивать, обобщать их, развивает память, наряду с этим развивает и гибкость мышления, учится контролировать свои рассуждения. [20,128] Рассмотрим основные виды устных упражнений.
Нахождение значений математических выражений. Предлагается в той или иной форме математическое выражение, требуется найти его значение. Эти упражнения имеют много вариантов.
Можно предлагать числовые математические выражения и буквенные (выражение с переменной), при этом буквам придают числовые значения и находят числовое значение полученного выражения. Например:
1) Найдите разность чисел 8,5-7,2.
2) Найдите значение выражения а+в, если а=0,06, в=0,92.
Выражения могут предлагаться в разной словесной форме: из 8,5 вычесть 7,2; 8,5 минус 7,2; уменьшаемое 8,5, вычитаемое 7,2, найти разность; найти разность чисел 8,5 и 7,2; уменьшить 8,5 на 7,2 и т. д. Эти формулировки использует не только учитель, но и ученики.
Выражения могут включать одно действие и более чем одно действие.
Основное назначение упражнений на нахождение значений выражений – выработать у учащихся твердые вычислительные навыки. Вместе с тем упражнения на нахождение значений выражений способствуют и усвоению вопросов теории арифметических действий.
Сравнение десятичных дробей. Эти упражнения имеют ряд вариантов. Могут быть даны два выражения, а надо установить, равны ли их значения, а если не равны, то какое из них больше или меньше. Например, предлагается сравнить выражения и вместо звездочки поставить знак «>», «>» или «=»:
2,7+0,9 * 0,9+2,7 55,7+7,6 * 55,7+0,3
0,5·10 * 0,7·15 2,4·9+2,4 * 2,4·10
При этом выбор знака отношения может быть выполнен либо на основе нахождения значений данных выражений и их сравнения (0,5·10<0,7·15, т. к. 5<10,5), либо на основе применения соответствующих знаний: переместительного свойства сложения 2,7+0,9 * 0,9+2,7, изменения результатов действий в зависимости от изменения одного из компонентов 55,7+7,6 * 55,7+0,3 и др.
Могут предлагаться упражнения, у которых уже дан знак отношения и одно из выражений, а другое выражение надо составить либо дополнить. Например, предлагается закончить запись: 8,1·(1,3+0,2)=8,1·1,3+…
Можно предлагать упражнения на сравнение выражений с переменной: например, а-1,7* а-1,2.
Главная роль таких упражнений – способствовать усвоению теоретических знаний об арифметических действиях, их свойствах, о равенствах, неравенствах и др. Кроме того, упражнения на сравнение выражений помогают и выработке вычислительных навыков.
Решение уравнений. Уравнения можно предлагать в разных формах:
1) Из какого числа надо вычесть 10,4, чтобы получить 4,7?
2) Найдите неизвестное число: 7,3-х=7,3-1,8.
3) Я задумала число, умножила его на 1,2 и получила 3,6. Какое число я задумала?
Назначение таких упражнений – выработать умение решать уравнения, помочь усвоить связи между компонентами и результатами арифметических действий, способствовать выработке вычислительных навыков.
Решение задач. Предлагаются задачи как простые, так и составные.
1) Периметр квадрата 9,6 ![]() . Найдите его сторону.
. Найдите его сторону.
2) Во сколько раз 4,8 больше 1,2?
3) Какое число меньше 3,3 в 3 раза?
4) Периметр квадрата 0,64 ![]() . Определите какова длина его стороны.
. Определите какова длина его стороны.
Цель данных упражнений выработка умений решать задачи, усвоение теоретических знаний, выработка вычислительных навыков.
В практике школы данные виды устных упражнений изменяются и дополняются самими учителями. Разнообразие упражнений возбуждает интерес у детей, активизирует их мыслительную деятельность.[2,166]
Предложенные устные задания помогут, особенно молодым учителям, привлечь внимание школьников на уроке и повысить их работоспособность в переходный период от начальной школы к средней.
Глава 2. Методика формирования вычислительных навыков у учащихся 5-го класса при изучении темы «Десятичные дроби»
2. 1. Разработка системы упражнений по формированию устных вычислительных навыков
Формирование вычислительных навыков - одна из главных задач, которая должна быть решена в ходе обучения детей в школе. Школа всегда уделяла большое внимание проблеме формирования прочных и осознанных вычислительных умений и навыков. Программы по математике включают большой интересный материал по проблеме формирования прочных навыков вычислений, однако, по-прежнему некоторые вопросы понимания и отработки навыка арифметических вычислений являются для школьников довольно сложными.
Изучив теоретические материалы по формированию устных вычислительных навыков, автором работы была разработана система заданий и упражнений (см. Приложение № ). Эти разнообразные задания позволяют развивать математическую речь ученика, гибкость мышления, возможность находить свой способ решения. Они дают возможность каждому ребенку проявить активность в поисковой работе, активизируют мыслительную деятельность, умение находить какие-то особенности в решении различных видов примеров. Вместе с тем количество упражнений и заданий достаточно для формирования прочных вычислительных навыков.
В данной системе уделяется особое внимание различным формам работы – это фронтальные, групповые задания, работа в парах.
Данная система рассматривает основные вопросы по теме “Десятичные дроби”, изучаемые в 5-ом классе:
➢ Десятичная запись дробных чисел;
➢ Сравнение десятичных дробей;
➢ Сложение десятичных дробей;
➢ Вычитание десятичных дробей;
➢ Приближенные значения чисел. Округление десятичных дробей;
➢ Умножение десятичных дробей на натуральные числа;
➢ Деление десятичных дробей на натуральные числа;
➢ Умножение десятичных дробей;
➢ Деление десятичных дробей.
Основная цель устных упражнений в данной системе – научить всех учеников производить в уме арифметические действия в пределах сложности примеров на сложение, вычитание, умножение и деление десятичных дробей. Задача учителя при этом – наряду с усвоением новых понятий и разделов математики сохранить трепетное отношение к числу, учить рациональным приемам счета, иногда дополняя материал учебника рассмотрение свойств действий (вычитание числа из суммы, вычитание суммы из числа, делимость произведения на число, делимость числа на произведение и т. д.).
Для того чтобы доказать или опровергнуть, что использование устных упражнений на уроках математики формирует вычислительный навык, автором работы была проведена практическая работа по использованию серии упражнений в 5-ом классе МОУ “Атнягузинская средняя общеобразовательная школа», учителем математики которого является Матынова Глафира Гадиловна.
Приведем фрагменты проводимых уроков с использованием различных видов устных упражнений.
Урок в 5 классе МОУ «Атнягузинской средней общеобразовательной школы».
Тема: Десятичная запись дробных чисел
Цели: научить читать и записывать десятичные дроби, переводить обыкновенную дробь со знаменателем 10, 100, 1000 и т. д. в десятичную дробь и наоборот; развивать вычислительные навыки, память, математическую речь, воспитывать интерес к математике и географии.
Оборудование: «вычислительные машины» у каждого ученика (в виде прямоугольного листочка бумаги с 4 кружочками), картинка или иллюстрация с изображениями планет.
I. Организационной момент
Сегодня наш урок будет необычным. Мы отправимся в путешествие в другую планету.
II. Устные упражнения
- Ребята, какие планеты вы знаете? Вообще существуют 9 планет: Земля, Марс, Юпитер, Венера, Сатурн, Нептун, Уран, Плутон, Меркурий. Мы с вами живем на планете Земля, но сегодня на уроке некоторые из вас отправятся на планету Юпитер (показываю эту планету на иллюстрации).Что же нужно сделать, чтобы попасть на эту планету?
Во-первых, у вас на партах у каждого лежит вычислительная машина. В эту машину вы после каждого задания устного счета будете записывать число. В конце у каждого на вычислительной машине появится код. С помощью этого кода мы проверим, кто отправился в путешествие, а кто остался в классе. Итак, за работу!
1. Найдите в каком номере пропущена ошибка, номер примера поставьте в первом кружочке вычислительной машины.
1) 15:5·13=39;
2) 17·5-11=64;
3) 33+27:3=20
2. Найдите верное утверждение и поставьте его номер во второй кружок вычислительной машины: Чтобы найти уменьшаемое, надо:
1) к разности прибавить вычитаемое;
2) из вычитаемого вычесть разность.
3. Назовите целую и дробную часть чисел: 1![]() ; 2
; 2![]() ; 7; 1
; 7; 1![]() ;
; ![]() . Запишите в третьем кружке машины натуральное число в ряде данных чисел.
. Запишите в третьем кружке машины натуральное число в ряде данных чисел.
4. Решите задачу, ответ запишите в последний кружок машины: Если 16 человек купили мороженное по цене 6 руб., то стоимость их покупки составил ... рублей.
- Теперь проверим, какой код получился у вас, и узнаем, кто может спокойно лететь на Юпитер, а кому еще нужно внимательно слушать учителя и больше заниматься математикой.
III. Объяснение нового материала
IV. Первичное закрепление материала
V. Итог урока: игра «Математическая эстафета»
Ученики, сидящие за первыми партами, жюри. Ученики с последних парт выходят к доске, выполняют задание и передают мел следующему. Задание: записать в виде десятичной дроби числа:
| I вариант | II вариант | ||
| 1 | 20 | 2 | 11 |
|
| 5 |
| 7 |
|
|
|
|
|
| 9 |
| 1 |
|
Анализ урока
Тип урока – урок изучения нового материала. Цели и задачи урока выполнены. Изучение темы начинается с организационного момента. Все учащиеся были хорошо подготовлены к уроку. Была осуществлена связь с географией (межпредметная связь). Этап отработки вычислительных навыков проводится в виде игры – путешествия в другую планету, так как именно игра является одним из средств формирования устных вычислительных навыков учащихся. Используя на уроке игру-путешествие в планету Юпитер, смогла заинтересовать учащихся с самого начала урока. Все этапы урока взаимосвязаны, каждый этап заканчивался микрообобщением. Время было распределено рационально, все учащиеся были вовлечены в работу.
Урок в 5 классе МОУ «Атнягузинская средняя общеобразовательная школа»
Тема: Сравнение десятичных дробей
Цели урока: - научить определять, находить равные дроби, сравнивать десятичные дроби; развивать математическую речь, навыки устных вычислений, учить детей правильной самооценке.
Оборудование: гость урока – белочка (можно нарисованную в дупле)
I. Организационный момент
Прозвенел звонок веселый.
Всех зовет он на урок.
Ну-ка, дети, все готовы?
Начинаем точно в срок.
На места все тихо сядем,
Не нарушим тишину.
Приготовились все слушать,
Я урок сейчас начну.
II Устные упражнения
1. Игровой момент «Где живет белка?»
- Ребята, сегодня на урок к нам пришла гостья. А кто эта гостья, вы узнаете, если отгадаете мою загадку.
Пышный хвост торчит с верхушки.
Что за странная зверюшка?
Щелкает орешки мелко,
Ну, конечно, это...(белка)
- Правильно, ребята, это белочка – замечательный зверек. Ребята, а где может жить белочка? (В норе, дупле или гнезде.) Решив эту цепочку, мы узнаем, где она живет. Если белочка живет в норе, то у вас получится число 8, если в дупле – то 5, а если в гнезде – то 6. (Учитель записывает на доске: в норе- 8; в дупле-5; в гнезде-6)
- Итак, давайте вместе решим эту цепочку:
2. Математический диктант «Торопись, да не ошибись» (включается магнитофонная запись, ученики выполняют диктант на листочках)Задание: запишите десятичные дроби: 2,8; 3,74; 1,371; 0,55; 145,003; 20,036; 201,0101; 6,006; 33,0008; 7,0034; 765,0945; 5674,76027.
III. Сообщение темы и целей урока
IV. Работа по теме урока
V. Итог урока: Выясните, в каком столбике верно записано число. Напишите в кружке букву, ему соответствующую.
| 1) пять целых две десятых | 5,02 Т | 5,2 Р | 5,002 П |
| 2) нуль целых восемь тысячных | 0,008 О | 0,08 Е | 0,8 У |
| 3) три целых двадцать пять тысячных | 3,25 Д | 30,25 В | 3,025 Т |
| 4) шестнадцать целых пять сотых | 16,005 А | 16,5 Е | 16,05 О |
| 5) восемнадцать целых восемь сотых | 18,8 Ш | 18,08 К | 18,008 В |
| 6) пять целых пятнадцать десятитысячных | 5,0015 А | 5,015 У | 5,15 И |
| 7) тридцать четыре целых сто пять тысячных | 34,0105 В | 34,105 С | 34,15 М |
Полученное слово - «РОТОКАС» означает название самого короткого в мире алфавита. В нем насчитывается 11 букв, и он используется жителями Папуа Новой Гвинеи.
- Сколько букв содержит русский алфавит? (33)
- Буквы какого алфавита используется для обозначения точек, отрезков, прямых? (Морзе)
Анализ урока
Тип урока – урок повторения знаний учащихся. Цели урока достигнуты, удалось решить на необходимом уровне поставленные задачи, повторить ранее изученный материал. Этап отработки вычислительных навыков проводится в виде таких средств формирования устных вычислительных навыков, как математический диктант и игровой момент. Была осуществлена межпредметная связь (связь с биологией, русским языком, историей). Используя данные задания в игровой форме, заметила заинтересованность детей, их внимательность, сосредоточенность к устным вычислениям. Ученики высказывают свое мнение только при поднятии руки и при разрешении учителя.
Урок в 5 классе МОУ «Атнягузинская средняя общеобразовательная школа»
Тема: Сложение и вычитание десятичных дробей
Цели урока: повторить изученный материал, закрепить навык сложения и вычитания десятичных дробей; развивать навыки устных вычислений, логическое мышление; воспитывать аккуратность, внимание.
Оборудование: конверт, карточки с числовыми выражениями, нарисованные Чебурашка и Шапокляк, набор магнитов.
I. Организационный момент
Ну-ка в сторону карандаши!
Ни костяшек, ни ручек, ни мела:
Устный счет! Мы творим это дело
Только силой ума и души!
Числа сходятся где-то во тьме
И глаза начинают светиться!
И кругом только умные лица!
Устный счет! Мы считаем в уме!
II Устные упражнения
1) Прочитайте дроби: 6,23; 98,704; 7,024; 8,003; 10,0208; 4,0004; 24,2009.
2) Сравните дроби: 6,37 и 6,299; 10,01 и 10,099; 9,18 и 9,1798;
7,01 и 7,018; 9,004 и 9,04; 28,028 и 28,0209.
3) Игровой момент
- Ребята, Чебурашка и Шапокляк прислали нам несколько выражений. Но в конверте все выражения перепутались и теперь мы не знаем, где решения Чебурашки, а где «ловушки» Шапокляк. Поэтому мы не можем быть уверены, что все решения верны, так как Шапокляк любит делать мелкие пакости. Наша задача обсудить выражения и их значения и обнаружить ошибки, если таковые имеются.
Содержание: 21,6+4,7=25,3; 6,7-3,9=2,8; 8,2+1,91=9,11; 5,84-2,7=3,16; 8-3,8=5,2;
- Работаем в парах. Вам необходимо просмотреть все действия, обнаружить ошибки, объяснить их своему соседу и, доказательно рассуждая исправить их. Итак, сколько вычислений прислал Чебурашка? (Одно). Вы смогли обнаружить и устранить «ловушки» Шапокляк? Молодцы! Это поможет нам не допускать ошибки и быть более внимательными.
Анализ урока
Повторительно-обобщающий урок по теме «Сложение и вычитание десятичных дробей». Одна из главных задач для учителя на данном уроке - это проверка устных приемов сложения и вычитания десятичных чисел. Поставленные цели урока были реализованы. Выбранные упражнения оказались оптимальными для реализации целей урока, способствовали формированию вычислительных навыков учащихся. На уроке развивала логическое мышление, внимание, память, активность учащихся, чередовала письменные виды деятельности с устными.
Урок в 5 классе МОУ «Атнягузинская средняя общеобразовательная школа
Тема: Умножение десятичных дробей на натуральные числа
Цели урока: закрепить навык умножения десятичной дроби на натуральное число, в том числе и на 10, 100, 1000 и т. д.; развивать математическую речь, навыки устных вычислении, внимание, память; воспитывать интерес к математике.
Оборудование: нарисованный медведь, дерево, телефон, жетоны, магниты, карточки
I. Организационный момент
Тот из вас мне всех милее,
Кто считает всех милее.
II. Устные упражнения
1. Игровой момент
- Ребята, посмотрите, у нас гость! Это – Михаил Потапович. Он пытается дозвониться лесным жителям: Айболиту, Бабе-Яге, Белоснежке и гномам, Царевне-лягушке. Но все номера телефонов смыл вчерашний дождь, и теперь ему никак не дозвониться ни к одному лесному жителю. Но скажу вам по секрету: если мы очень постараемся и выполним все задания устного счета, то поможем узнать Михаилу Потаповичу все номера лесных жителей. Итак, за дело.
1. Вычисли:
53,25+5,75; 25,005-2,005; 34,1005-13,1005.
Постепенно на доске появляется номер телефона Айболита:
2.Округлите данные числа до единиц: 13,547; 87,0125; 60,411.
На доске появляется номер телефона Бабы-Яги:
3. Заполните таблицу:
| I слагаемое | 7,8 | 8,65 | |
| II слагаемое | 6,43 | 1,35 | |
| Сумма | 9,8 | 11,43 |
Учитель записывает на доске номер телефона Белоснежки и гномов.
Похожие работы
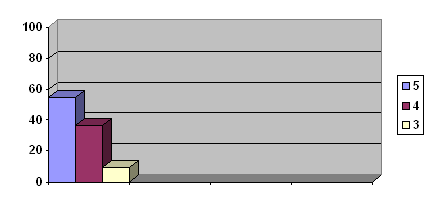
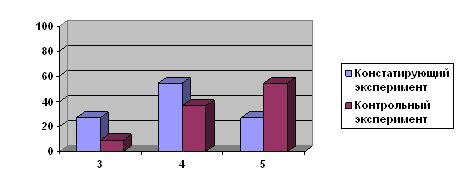
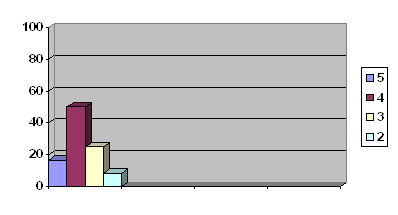
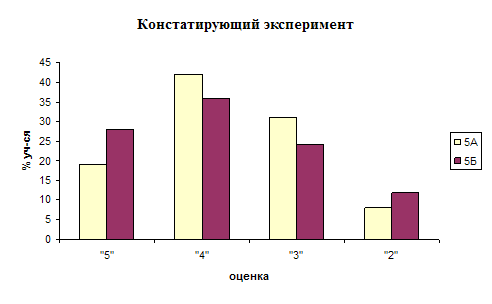
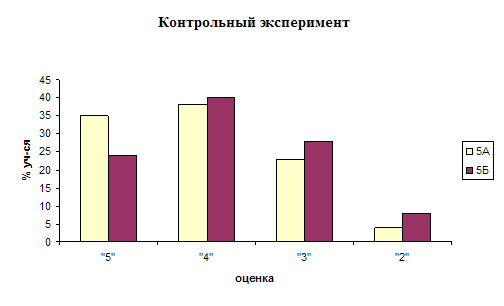
... показал, что на начало эксперимента, качество знаний у учащихся находится на одном уровне. 2. Формирующий эксперимент. Цель: повышение качества знаний учащихся 5 «А» класса при помощи мультимедийного проектора. В экспериментальном - 5 «А» классе проводились уроки с использованием мультимедийного проектора. Они были направлены на повышение качества знаний учащихся. В контрольном – 5 «Б» классе ...
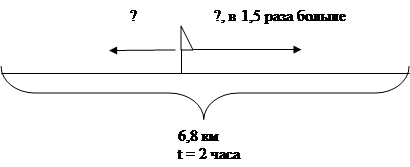
... искомой величины в зависимости от изменения данных величин; помогает сделать обобщения теоретических знаний; развивает самостоятельность и вариативность мышления. Использование моделирования при работе над задачами на движение в 5 классе Использование моделей при решении задач на движение по теме «Десятичные дроби» (учебник «Математика» автор Н. Я. Виленкин) Задача 1: (№ 1142) «Из ...
... имеют достаточно четкое и правильное представление из собственного жизненного опыта, а формулировки которых являются слишком громоздкими. Выводы по § 1 1. Основные цели изучения темы «Объемы многогранников» в курсе стереометрии – развитие пространственных представлений учащихся, освоение способов вычисления практически важных величин и дальнейшее развитие логического мышления учащихся. ...
... наиболее существенных чет, характеризующих общую готовность человека к труду. Глава 2. Исследование влияния дидактических игр на развитие внимания 2.1. Использование дидактических игр на уроках математики в 5 классе Изучив теоретический материал по использованию дидактических игр для развития внимания у учащихся, у автора возникло желание и интерес реализовать это на практике. Автором ...

0 комментариев