Выбор тормозного резистора

5.6 Выбор тормозного резистора

На тормозном резисторе рассеивается энергия, передаваемая из двигателя в звено постоянного тока преобразователя частоты при торможении. Он необходим для качественного и быстрого торможения. Для проектируемого электропривода в нормальном режиме работы время торможения не лимитируется. Однако торможение электропривода в аварийном режима должно происходить как можно быстрее. Поэтому заложим в проектируемый электропривод тормозной резистор.

Расчет сопротивления тормозного резистора будем производить по методике фирмы «Danfoss» [13].

Для расчета сопротивления необходимо определить пиковую мощность:

Р_РЕК=Р_м*М_BR(%)*η_м*η_VLT,

где: Р_м – мощность приводного двигателя;

М_BR(%) – соотношение от номинального, вращающегося момента. Принимаем М_BR(%)=160%,

η_м – КПД двигателя,

η_VLT – КПД преобразователя частоты.

Р_РЕК=1500*1.6*0.77*0.96=1774 Вт.

Тормозное сопротивление рассчитывается по формуле:

,

где: U_DC – напряжение в промежуточной цепи инвертора. Принимаем U_DC=810В

6.  ПРОЕКТИРОВАНИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

6.1 Математическое описание объекта управления

6.1.1 Математическое описание асинхронного электродвигателя из уравнений обобщенной машины

Электромеханический преобразователь (ЭМП) в структуре электропривода представляет собой идеализированный двигатель, ротор которого не обладает механической инерцией, не подвержен воздействию момента механических потерь и жестко связан с реальным ротором, входящим в состав механической части электропривода. Исследование процессов в ЭМП энергии обычно выполняют не непосредственно на конкретной конструкции, а на эквивалентных моделях. Благодаря тому, что в основе работы ЭМП автоматизированных электроприводов лежат одни и те же законы, появляется возможность создать универсальные общие модели для различных типов преобразователей. В этом смысле вращающиеся преобразователи можно разделить на две большие группы:

1)  Преобразователи, у которых токи (или магнитные потоки) взаимно перемещающихся частей создаются с помощью источников энергии переменного тока.

2)  Преобразователи, у которых одна часть (статор или ротор) возбуждаются от источника переменного тока, а другая – от источника постоянного тока.

Одной из наиболее распространенных технических реализаций ЭМП первой группы являются асинхронные машины. Ограничив рассмотрение только трехфазными машинами, используем следующие общепринятые допущения:

1)  Параметры обмоток фаз ротора и статора соответственно одинаковы, а система напряжений фаз симметрична;

2)  Магнитопроводы ненасыщены;

3)  Воздушный зазор между взаимно перемещающимися частями ЭМП равномерный;

4)  МДС в воздушном зазоре синусоидальна;

5)  Влияние потерь в стали и эффекта вытеснения тока и потока на характеристики ЭМП не учитывается;

6)  Обе части ЭМП имеют однотипные распределенные обмотки.

При других исполнениях одной из частей ЭМП (беличья клетка) ее параметры можно привести к эквивалентной распределенной обмотке. На рис. 6.1 дана первичная модель асинхронной трехфазной машины, изображаемая обычно в плоскости, перпендикулярной оси вала. Здесь условно изображены сечения обмоток фаз статора (присвоен индекс 1) и ротора (присвоен индекс 2), и оси этих обмоток, перпендикулярные их плоскостям. При подключении обмоток к источникам трехфазного переменного напряжения токи в обмотках будут определяться уравнениями равновесия напряжений:

 (6.1)

где: Ψ – полное потокосцепление обмоток соответствующих фаз,

R – активное сопротивление обмоток,

i – фазные токи обмоток,

u – фазные напряжения обмоток.

ЭДС dΨ/dt определяются изменением короткосцепленных обмоток во времени как под действием соответствующих токов во времени, так и под действием взаимного перемещения обмоток статора и ротора.

Поведение каждой из переменных исходной (приближенной к реальной конструкции) модели (рис 6.1) может быть описано как изменение во времени эквивалентных векторов переменных, направленных по осям фаз. Такому описанию соответствует эквивалентная модель машины, где реальные обмотки заменены эквивалентными сосредоточенными катушками, расположенными по осям фаз (рис. 6.2) и обладающими параметрами обмоток фаз. Для каждой фазы такой модели соотношение переменных удобно показать на векторной диаграмме, построенной для произвольно фиксированной частоты с учетом принятых ранее допущений (рис. 6.3).Кроме того, при построении векторной диаграммы параметры ротора были приведены к параметрам статора, а диаграмма построена для фиксированного момента времени, когда вектор фазного напряжения совпадает с осью фазы при вращении векторов против часовой стрелки. Эта диаграмма представляет своего рода математическую абстрактную модель, основанную на известном в электротехнике приеме изображения гармонических функций в виде вращающихся временных векторов. Реальные временные соотношения между переменными фазы определяются проекциями вращающихся векторов на ось фазы, а временные фазовые сдвиги между переменными соответствуют углам между векторами. Следует отметить, что для упрощения диаграмма построена для машины, возбуждаемой только со стороны статора.

Все векторы на диаграмме соответствуют реально существующим переменным, кроме намагничивающего тока I_m. Этот ток определяет по модулю и фазе часть тока статора, которая проходя через обмотку с индуктивностью, равной взаимной индуктивности фаз статора и ротора L_m, создает в воздушном зазоре ЭМП рабочее потокосцепление Ψ_m. Полное же потокосцепление каждой

катушки (см рис. 6.2) определяется суммой рабочего потокосцепления и потокосцепления рассеяния (Ψ_1σ или Ψ_2σ). Поскольку потокосцепления определяются совокупным действием всех токов, то для мгновенных значений переменных фазы можно записать:

;

 (6.2)

.

Здесь L₁=L_m+L_1σ; L₂=L_m+L_2σ; L₁, L₂ – полные индуктивности статора и ротора соответственно; L_1σ, L_2σ – индуктивности рассеяния соответствующих фаз; L_m – взаимная индуктивность фаз статора и ротора, причем L_m в трехфазных машинах, благодаря взаимному влиянию всех трех фаз, в 3/2 раза больше взаимной индуктивности фаз статора и ротора при их соосном расположении.

Поскольку рабочее потокосцепление является общим для обмоток, как статора, так и ротора, то на основании (6.2), раскрывая полные индуктивности, можно записать для каждой фазы:

;

.

Так как без учета активной составляющей тока холостого хода İ₁+İ₂≈İ_µ, получим:

; (6.3)

.

Таким образом, рабочее потокосцепление можно выразить непосредственно через сумму токов статора и ротора:

. (6.4)

В уравнениях (6.2) – (6.4) все переменные – функции времени, выраженные через соответствующие временные векторы.

Под действием рабочих потокосцеплений обмоток всех (в нашем случае трех) фаз машины в воздушном зазоре формируется вращающееся магнитное поле, которое можно описать вращающимся эквивалентным пространственным вектором в плоскости, перпендикулярной оси вала. Учитывая, что переменные величины описываются временными векторами, пульсирующими по осям фаз (рис. 6.2), примем за начало отсчета времени момент прохождения рабочего потокосцепления фазы а через нулевое значение. Тогда для мгновенных значений рабочих потокосцеплений фаз можем записать:

  ;

  ; (6.5)

.

Считаем машину двух полюсной, что общепринято при построении математических моделей. В этом случае угловая частота сети ω₁ будет соответствовать угловой скорости магнитного потока в воздушном зазоре и, соответственно, синхронной скорости ротора. Задав вначале ω₁t=0 и для простоты построений приняв Ψ_mmax=1, из (6.5), получим Ψ_ma=0; Ψ_mb=-; Ψ_mc=. Учитывая, что рабочие потокосцепления фаз ориентированы по осям фаз и, сложив их геометрически, получим (6.6) – результирующий пространственный вектор Ψ₁ для момента времени ω₁t=0 (рис. 6.4). Проделав ту же операцию для ряда последовательных значений ω₁t (ω₁t=60° и т.д.), можно показать, что результирующий пространственный вектор будет вращаться со скоростью ω₁t, а его амплитуда в  раза больше модуля соответствующего временного вектора фазы.

Таким же образом мы можем получить результирующие пространственные всех электромагнитных переменных машины. Поскольку при формировании результирующих векторов геометрически складываются соответствующие временные векторы, ориентированные в пространстве по осям фаз и имеющие одинаковые фазовые сдвиги относительно других временных векторов собственной фазы, конфигурация пространственной векторной диаграммы машины будет такой же, как и у временной диаграммы фазы. На рис. 6.3 приведена пространственная временная диаграмма асинхронной машины при ее возбуждении только со стороны статора. Поскольку характеристики ЭМП определяются изменением амплитуд и взаимной ориентации векторов переменных, на рис. 6.5 начальная фаза векторов выбрана произвольно относительно координатных осей x, y, причем эти оси вращаются в пространстве с угловой скоростью ω₁. Кроме того, пространственный угол δ между результирующими векторами рабочего потокосцепления и тока ротора по аналогии с синхронными машинами будем называть углом нагрузки. Так же принята система обозначений координатных осей: х – продольная ось, у – поперечная ось.

Для пространственной векторной модели, так же как и для первичной модели, можно написать уравнения равновесия напряжений:

 ;

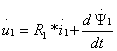 (6.6)

.

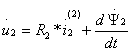Здесь, как и на рис. 1.6  -- пространственные векторы. Однако такие уравнения непосредственно нельзя решать совместно, поскольку переменные статора записаны в статорной системе координат, а переменные ротора (помечены верхним индексом (2)) в роторной системе, т.е. вращаются относительно статора с угловой скоростью ω. В результате оси статора и ротора сдвинуты относительно друг друга на переменный угол θ(t). Для того, чтобы привести уравнение роторной цепи к неподвижным осям статора, необходимо вектор потокосцепления ротора домножить на оператор поворота е^-jθ, а затем «заставить» все векторы уравнения ротора вращаться быстрее относительно ротора, увеличив их скорости на угловую скорость ротора, т.е. умножить все члены уравнения ротора на оператор е^jθ. Тогда получим:

,

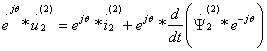или:

,

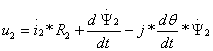где все величины записаны в координатах статора.

Учитывая, что , систему (6.6) перепишем в неподвижных координатах статора:

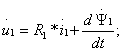
(6.7)

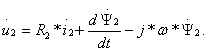
Поскольку корректность математических моделей не зависит от выбора координатных осей, но вид координат может упростить анализ, обычно в зависимости от объекта и задач исследования выбирают одну из трех координатных систем: неподвижную (6.7), синхронно вращающуюся в пространстве со скоростью поля статора или вращающуюся со скоростью ротора. Чтобы привести уравнение (6.7) к координатам, вращающимся в пространстве в общем случае с произвольной скоростью ω_ĸ, можно воспользоваться тем же приемом, домножив переменные векторы на оператор поворота , где θ_k – угол между координатной системой и пространственными векторами. Тогда получим:

 ;

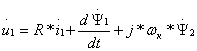 (6.8)

,

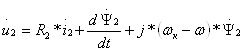где:

;

(6.9)

.

В уравнениях (6.6) – (6.9) индекс принадлежности к координатным системам опущен, однако следует помнить, что они записаны в различных координатных системах.

При анализе удобнее использовать не непосредственно векторные уравнения, а уравнения в проекциях векторов на координатные оси. Обозначив эти оси х и у, запишем систему (6.8) в проекциях на оси:

;

;

 (6.10)

;

.

В этой системе уравнений четыре неизвестных тока и четыре потокосцепления. Для решения системы следует электромагнитные переменные выразить либо через потокосцепления, либо через токи. Выразим потокосцепления через токи, для чего спроецируем векторы потокосцеплений (6.9) на координатные оси:

;

;

;

.

Учитывая симметрию асинхронной машины по осям х, у, перепишем (6.11) в виде:

;

;

(6.11)

;

.

Электромагнитный момент, возникающий при взаимодействии токов и потоков взаимно перемещающихся частей ЭМП независимо от способов их возбуждения, определяется векторным произведением результирующего вектора рабочего потокосцепления в воздушном зазоре и результирующего вектора тока одной из частей ЭМП, например:

. (6.12)

Учитывая, что в ЭМП электромагнитные переменные взаимозависимы, электромагнитный момент можно выразить через любую пару векторов. Подставив (6.4) в (6.12), получим:

. (6.13)

Заменив в (6.13) i_m на i₁+i₂, получим:

. (6.14)

Проектируя векторное уравнение (6.14) на координатные оси х, у, получим для момента:

. (6.15)

При переходе к двухфазной модели согласно [18], выражение для электромагнитного момента запишем в виде:

. (6.16)

Движение механической части электропривода описывается уравнением:

.

Запишем систему уравнений, описывающих электромеханические и механические процессы в асинхронном двигателе:

;

;

;

;

;

(6.17)

;

;

;

;

.

Похожие работы

Оборудование предприятий общественного питания

Скачать

162367

1

1

... работник, и автоматизированные, где контроль за безопасной работой и режимом тепловой обработки обеспечивает сам тепловой аппарат при помощи приборов автоматики. На предприятиях общественного питания тепловое оборудование может использоваться как несекционное или секционное, модулированное. Несекционное оборудование, это оборудование, которое различно по габаритам, конструктивному исполнению и ...