Навигация
Построение статических характеристик электропривода
6.4 Построение статических характеристик электропривода
По уравнению (6.19) построим естественную электромеханическую характеристику электропривода:
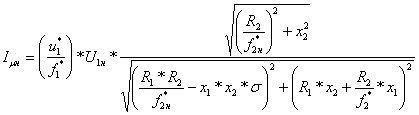 . (6.42)
. (6.42)
Результаты расчета представлены в виде графика (рис.6.11).
Естественная механическая характеристика была построена в пункте 6.3.
Для построения искусственных статических характеристик на основании структурной схемы запишем выражение для напряжения:
![]() . (6.43)
. (6.43)
Подставим в (6.43) выражение для тока (6.19):
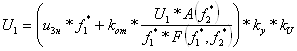 . (6.44)
. (6.44)
Из уравнения (6.44) выразим U1 и запишем выражение:
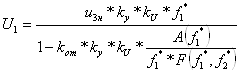 . (6.45)
. (6.45)
При построении искусственных статических характеристик следует учесть ограничение подводимого к электродвигателю напряжения. Напряжение U1 будем ограничивать на уровне U1max=1.1 U1н.
Составим систему уравнений для построения искусственных механических и электромеханических характеристик электропривода:
![]()
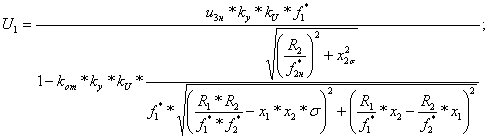
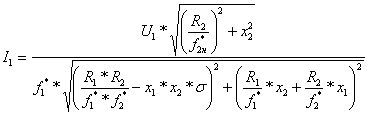 ;
;
(6.46)
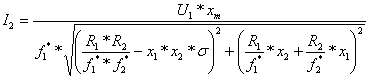 ;
;
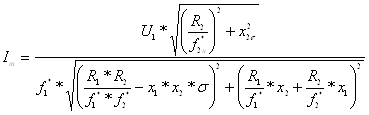 ;
;
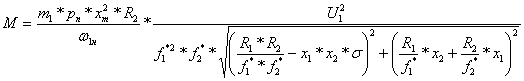 .
.
Построим по системе (6.46) статические характеристики для двух скоростей ![]() и
и ![]() . Результаты расчета представлены в виде графиков (рис. 6.11, 6.12).
. Результаты расчета представлены в виде графиков (рис. 6.11, 6.12).
6.5 Проверка электродвигателя по нагреву при работе на нижней скорости
Известно, что у само вентилируемых двигателей ухудшаются условия охлаждения при снижении частоты вращения. Поэтому необходимо проверить, соблюдаются ли условия по нагреву при работе на нижней скорости диапазона регулирования. Расчет допустимого момента по условиям нагрева будем
производить по методике, изложенной в [8].
Известно, что лимитирующей по нагреву частью асинхронного короткозамкнутого двигателя в установившемся режиме является изоляция обмотки статора. Среднее установившееся превышение температуры обмотки статора может быть определено по методу эквивалентных потерь, согласно которому уравнение теплового баланса записывается следующим образом:
![]() , (6.47)
, (6.47)
где: τ∞ – установившееся превышение температуры статора;
![]() – теплоотдача, зависящая от угловой скорости;
– теплоотдача, зависящая от угловой скорости;
![]() – коэффициенты внешнего подогрева, учитывающие долю внешних потерь, участвующих в нагревании обмотки статора, в общем случае зависящие от скорости.
– коэффициенты внешнего подогрева, учитывающие долю внешних потерь, участвующих в нагревании обмотки статора, в общем случае зависящие от скорости.
![]() ,
(6.48)
,
(6.48)
![]() , (6.49)
, (6.49)
![]() ,
,
![]() .
.
Распишем выражения для ΔPM1, ΔPM2, ΔPcm:
 (6.50)
(6.50)
![]() ; (6.51)
; (6.51)
![]() , (6.52)
, (6.52)
где: ΔPсmвн – номинальные потери в стали на вихревые токи;
φ – относительное значение потока;
ΔPсmгн – номинальные потери в стали на гистерезис.
Перепишем (6.42) в виде:
![]() . (6.53)
. (6.53)
Для номинального режима уравнение (6.53) примет вид:
![]() ,
,
или
![]() , (6.54)
, (6.54)
где: hτ – доля эквивалентных греющих потерь при номинальном режиме.
Поделив почленно (6.53) на (6.54), получим уравнение теплового баланса при частотном управлении в относительных единицах:
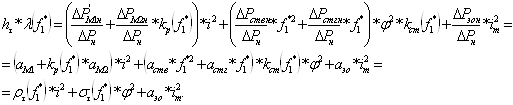 (6.55)
(6.55)
Примем допущение [8]:
![]() , (6.56)
, (6.56)
где: μ – относительное значение момента.
Подставим (6.56) в (6.55) и выразим μ:
 . (6.57)
. (6.57)
Определим значения постоянных коэффициентов:
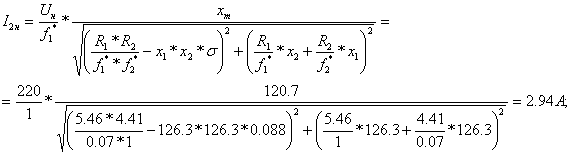
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Примем из [8] ![]() , тогда:
, тогда:
![]() ,
,
![]() .
.
Выразим из (6.21) формулу для определения относительного тока намагничивания im:
 . (6.58)
. (6.58)
Т.к. электропривод работает в установившемся режиме с нагрузками меньше номинальной, то примем φ=im.
Запишем выражение для ![]() – коэффициент изменения теплоотдачи:
– коэффициент изменения теплоотдачи:
![]() ,
,
где: λ0 – коэффициент теплоотдачи для неподвижного двигателя. Примем λ0=0.4 из [8]. Запишем систему уравнений для определения μ:
![]()
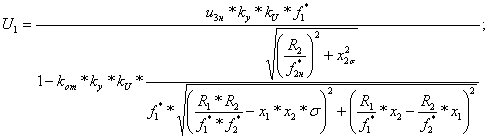
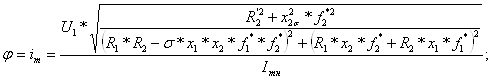
![]()
(6.59)
![]() ;
;
![]() ;
;
 ;
;
По системе уравнений (8.37) построим зависимость допустимого по
нагреву момента от частоты питающего напряжения, приняв ![]() . Результаты расчета представлены в виде графика на рис. 6.13. Определим, какой допустимый момент можно иметь с АД на нижней скорости диапазона регулирования.
. Результаты расчета представлены в виде графика на рис. 6.13. Определим, какой допустимый момент можно иметь с АД на нижней скорости диапазона регулирования. ![]() . Из рис. 6.13 видно, что μ(
. Из рис. 6.13 видно, что μ(![]() )≈0.7.
)≈0.7.
![]() .
.
Следовательно, данный двигатель удовлетворяет условиям нагрева, т. к. Мдоп>Мсm=5.1H·м
Похожие работы
... работник, и автоматизированные, где контроль за безопасной работой и режимом тепловой обработки обеспечивает сам тепловой аппарат при помощи приборов автоматики. На предприятиях общественного питания тепловое оборудование может использоваться как несекционное или секционное, модулированное. Несекционное оборудование, это оборудование, которое различно по габаритам, конструктивному исполнению и ...
0 комментариев