Математическое описание асинхронного электродвигателя в установившихся режимах

6.1.2 Математическое описание асинхронного электродвигателя в установившихся режимах

Для анализа свойств асинхронных двигателей в установившихся режимах обычно используют схему замещения фазы машины (рис. 6.7), соответствующую векторной диаграмме, приведенной на рис. 6.3 и общепринятые допущения, сформулированные ранее. На рис. 6.7.а символ S обозначает скольжение, а остальные обозначения были использованы ранее. Однако эта схема неудобна для анализа при переменной частоте, поскольку все сопротивления, кроме активного сопротивления обмотки фазы статора R₁, являются функциями частоты. Поэтому, введя понятие относительной амплитуды  и относительной частоты , выделим переменные и параметры, перейдя к схеме замещения на рис.6.7.б. Здесь все индуктивные сопротивления соответствуют номинальной частоте питающего напряжения машины [ ]. Кроме того, скольжение S при переменной частоте не определяет однозначно степени нагрузки машины, являясь еще и функцией частоты напряжения на статоре. Поэтому его удобнее выразить через относительные частоты:

, (6.18)

где:  – абсолютная и относительная частоты токов ротора.

Используя схему замещения, найдем выражения для действующих значений электромагнитных переменных. Ток фазы статора:

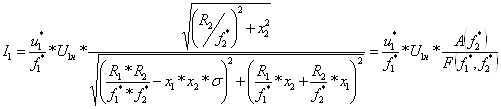 (6.19)

Здесь U_1н – номинальное фазное напряжение машины; х₁=х_m+х_1σ – полное индуктивное сопротивление контура статора при разомкнутом роторе; х₂=х_m+х_2σ – полное индуктивное сопротивление контура статора при разомкнутом статоре;  – коэффициент рассеяния.

Кроме того, нужно иметь в виду, что роторные величины приведены к статорным, хотя индекс приведения здесь и далее опущен.

Ток фазы ротора:

. (6.20)

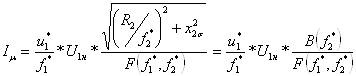
Намагничивающий ток:

. (6.21)

Потокосцепление в воздушном зазоре:

, (6.22)

где  -- конструктивная постоянная статора;

 k_об – обмоточный коэффициент;

 ω₁ – число последовательных витков одной фазы.

Уравнения электромагнитного момента можно получить, используя выражение либо для электромагнитной мощности, либо векторное уравнение (6.14). Рассмотрим первый путь.

Электромагнитная мощность будет:

.

Подставляя сюда выражения (6.18) – (6.20), находим:

,

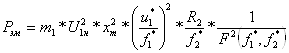при этом для момента можем записать:

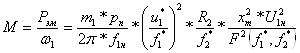. (6.23)

Уравнения (6.19) – (6.23) описывают электромеханические свойства двигателя в установившемся режиме.

6.1.3.  Составление структурной схемы частотно-регулируемого асинхронного двигателя

При исследовании асинхронных машин обычно используют одну из трех координатных систем: с привязкой осей к элементам конструкции статора (неподвижные оси); с привязкой осей к элементам конструкции ротора; оси, синхронно вращающиеся в пространстве. При этом основным принципом выбора координатной системы является простота математического описания электромагнитных процессов в машине.

При решении задач анализа и синтеза частотно-регулируемых электроприводов кроме этого принципа при выборе системы координат необходимо учитывать еще простоту математической модели автоматизированного электропривода, а это прежде всего определяется требованиями к управляемости, т.е. к качеству регулирования основных элементов – скорости и момента. С этих позиций координатные оси, ориентированные по элементам конструкции (статора или ротора), оказываются неудобными, поскольку в установившихся режимах электромагнитные переменные двигателя будут иметь частоты, отличные от нуля, а исследование системы придется выполнять на несущей частоте. С этих позиций для частотно-регулируемых электроприводов любого типа наиболее удобными являются координатные оси, синхронно вращающиеся в пространстве. В этом случае в установившихся режимах пространственные вектора электромагнитных переменных оказываются неподвижными относительно осей, а их проекции на оси – скалярными величинами, что позволяет при анализе и синтезе использовать методы и аппаратурные средства, хорошо разработанные для электроприводов с двигателями постоянного тока.

Более того, в синхронных осях появляется дополнительная возможность упрощения математических моделей как двигателя, так и электропривода в целом за счет привязки координатных осей к одному из пространственных векторов электромагнитных переменных. В зависимости от выбранного для ориентации координатных осей опорного вектора можно построить одну из семи структурных схем асинхронной машины – в координатах u₁, i₁, i_2, Ψ₁, Ψ₂, Ψ_m или e_r и соответствующие им структурные схемы частотно-регулируемых электроприводов. Если рассматривать структурные схемы только асинхронных двигателей с точки зрения их простоты и возможностей организации управления, предпочтительными являются структуры с ориентацией по Ψ₁, Ψ₂.Структуры с ориентацией по токам i₁, i₂ имеют наименьшее число перекрестных связей, однако формирование сигналов по ω₁ здесь наиболее сложно. Структура с орентацией по u₁ содержит большее число перекрестных связей и блоков умножения, но формирование входных воздействий здесь проще, чем в остальных структурах. В тоже время при выборе координатной системы для частотно-регулируемых приводов с короткозамкнутыми асинхронными двигателями следует учитывать, что ток ротора в таких системах измерить невозможно, а поэтому одной из целесообразных здесь могут быть структуры в координатах u₁, Ψ₂ или i₂.

Кроме того, при выборе координатной системы не следует забывать и о физической реализации самой системы. А с этих позиций, какие бы координатные системы не использовались при построении структурной схемы электропривода, аснхронный двигатель управляется амплитудой, фазой и частотой реальных фазных напряжени; поэтому чем больше преобразований претерпевают эти переменные при переходе к эквивалентной модели, тем больше координатных и функциональных преобразований необходимо выполнить в каналах формирования реальных сигналов управления, и эти усложнения должны быть технически оправданы. Следовательно, если иметь в виду электропривод с асинхронным короткозамкнутым двигателем, то окончательный выбор одной из координатных систем (u₁, Ψ₂, i₂ ) должен определяться требованиями к качеству регулирования в статических и динамических режимах.

Как известно, электромагнитные переходные процессы в асинхронном двигателе носят колебательный характер, причем колебания свободной составляющей электромагнитного момента определяются прежде всего колебаниями фазовых сдвигов токов. Поэтому в быстродействующих электроприводах, где качания электромагнитного момента жестко нормированы, необходимо организовать управление не только по амплитуде напряжений (токов), но и по фазе тока. В этом случае в системах с управлением по напряжению для частотно-регулируемых электроприводов с асинхронными короткозамкнутыми двигателями целесообразны структуры с ориентацией по Ψ₁. Если требования к быстродействию позволяют уменьшить амплитуду качаний момента за счет снижения форсировки, то можно воспользоваться координатами, ориентированными по u₁, и перейти на управление только по уровням напряжений, токов и потокосцеплений. В этом случае более сложная структурная схема двигателя оправдывается существенным упрощением информационной части системы.

 На основании выше изложенных рассуждений выбираем систему координат, вращающихся в пространстве с угловой скоростью вектора тока статора (х,у) и ось х с осью вектора напряжения . Тогда для описания электромагнитных процессов воспользуемся системой уравнений (6.17), учтя при этом: ω₂=ω₁–p_п*ω, u_1x=U_1m, u_1y=0:

;

;

;

;

;

(6.25)

;

;

.

Преобразуем систему (6.25) по Лапласу и получим:

;

;

;

;

;

(6.26)

;

;

 .

Преобразуем систему (6.26) к виду:

;

;

(6.27)

;

.

Выразим из (6.27) токи:

;

;

;

.

Разделим числитель и знаменатель первых двух уравнений на R₁, а вторых двух – на R₂, и введем обозначения постоянных времени:

.

;

;

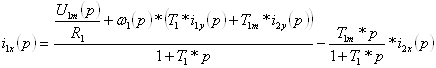(6.28)

;

.

Дополним систему (6.28) уравнением электромагнитного момента (6.16) и выразим скорость из уравнения движения, преобразуя, преобразуя их в операторную форму:

;

;

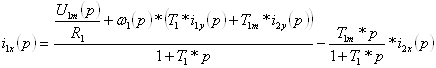(6.29)

;

;

;

.

По системе уравнений составим структурную схему асинхронного электродвигателя и механической части электропривода (графическая часть: лист 4).

Похожие работы

Оборудование предприятий общественного питания

Скачать

162367

1

1

... работник, и автоматизированные, где контроль за безопасной работой и режимом тепловой обработки обеспечивает сам тепловой аппарат при помощи приборов автоматики. На предприятиях общественного питания тепловое оборудование может использоваться как несекционное или секционное, модулированное. Несекционное оборудование, это оборудование, которое различно по габаритам, конструктивному исполнению и ...