Навигация
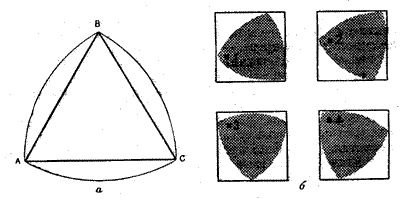
Площадь треугольника Рело
34249
знаков
0
таблиц
14
изображений
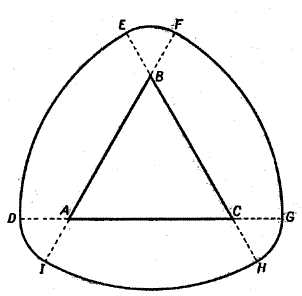
4.4 Площадь треугольника Рело
Одна из задач моей работы: доказать, что из всех фигур постоянной ширины d треугольник Рело имеет наименьшую площадь.
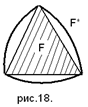
Для начала найдем площадь треугольника Рело:
;
;
Следовательно, площадь треугольника Рело равна
Попробуем доказать, что треугольник Рело имеет наименьшую площадь. Обозначим через n количество сторон многоугольника.
Пусть дан какой-то правильный n–угольник (с нечетным числом сторон), следовательно, его шириной будет наибольшая из диагоналей (в данном случае их две).
(при n
), 
.
Оценим 
и площадь треугольника Релло:
, 
>
Следовательно, 
больше площади треугольника Рело, а равносторонний, треугольник является многоугольником с наименьшим числом вершин (сторон). Значит, с увеличением числа вершин многоугольника площадь фигуры постоянной ширины, в которую вписан этот многоугольник, будет увеличиваться.
Попробуем доказать, что треугольник Рело имеет наименьшую площадь через n— количество сторон многоугольника.
Доказательство.
Итак, площадь треугольника Рело равна 
.
Пусть дан правильный многоугольник со стороной а. О — центр вписанной и описанной окружности. ОА=ОD; ОН
АD;
АОD=
(n-число сторон), т.к. треугольник равнобедренный, ОН –биссектриса угла АОD.
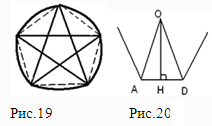
Следовательно,
АОН=НОD; 
АОН: АОН=
; АН=
, то 
.
.
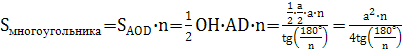Диаметром многоугольника является его наибольшая диагональ (в данном случае их две). Рассмотрим центральный угол АОВ и вписанный в окружность угол АМВ (рис. 21), то АОВ=2АМВ, АМВ=. AM=MB, то по теореме косинусов
, то
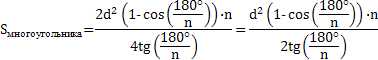
Площадь фигуры, в которую вписан правильный многоугольник состоит из площади многоугольника и суммы площадей равных сегментов. Площадь сегмента равна
(Sсегмента=Sсектора 
Sтреугольника АМВ).
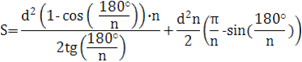
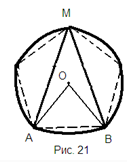
Остается доказать, что это выражение будет всегда больше площади треугольника Рело, т.е. больше чем
. Для этого вычтем из площади треугольника Рело площадь фигуры постоянного диаметра, в которую вписан правильный многоугольник и докажем, что эта разность при n>3 всегда будет отрицательной:
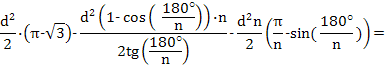
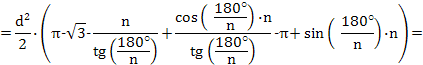
Итак, при любом n>3
Следовательно, разность площади треугольника Рело и площади фигуры постоянного диаметра, в которую вписан правильный многоугольник, отрицательна. Из всех фигур постоянной ширины треугольник Рело имеет наименьшую площадь.
Похожие работы
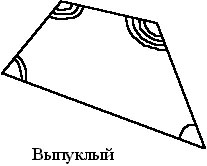
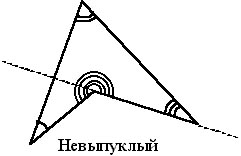
... меньше 180° (см. рисунок). Выпуклый многоугольник всегда расположен в одной полуплоскости относительно каждой прямой, проходящей через его сторону. Выпуклыми фигурами являются: треугольник, параллелограмм, трапеция, круг, эллипс (рис.1). На рис.2 приведены примеры невыпуклых фигур. Имеются полезные утверждения, которые ...
... характеристику основных знаний умений и навыков по данной специальности. Тифлопедагог дошкольного образовательного учреждения является ведущим специалистом, координирующим и направляющим коррекционно-педагогическую работу. В общем коррекционно-педагогическом процессе, осуществляемом в детском саду для детей с нарушением зрения, специальные коррекционные занятия тифлопедагога играют роль про ...
... контактов обеспечивается выбором их материала и конструкции при использовании одноступенчатой системы. В заключение отметим, что в настоящее время начинают широко применяться электрические аппараты с герметизированными контактами и контактами, работающими в глубоком вакууме. Жидкометаллические контакты? Наиболее характерные недостатки твердометаллических контактов следующие: 1. С ростом ...
... английский, можно ли сказать, что проблема евроцентризма ушла в прошлое? Очевидно, многое еще остается выяснить в наших подходах к мировой истории. РАЗДЕЛ 2. ТЕОРИЯ ЯДРА Глава 1 Центр и периферия цивилизации § 1. А. Тойнби О ТЕРРИТОРИАЛЬНОМ РАСПРОСТРАНЕНИИ КАК КРИТЕРИИ РАЗВИТИЯ ЦИВИЛИЗАЦИИ Рост цивилизации по своей природе является восходящим движением. Цивилизации развиваются ...
0 комментариев