Навигация
Введенную ранее дельта-функцию d (t) определим следующим образом
2. Введенную ранее дельта-функцию d (t) определим следующим образом
(d (t), j(t)) = j(0).
Исходя из интегрального представления (2), имеем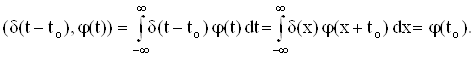
Если а(t) – непрерывная функция, то
(а(t) d(t), j(t)) = (d(t), а(t) j(t)) = a(o) j(o) ( j Î Ko).
Отметим, что функционал f , определенный на K соотношением
![]()
не является обобщенной функцией, так как, являясь непрерывным функционалом, он не линеен.
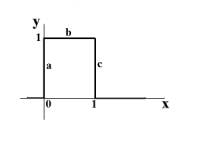
3. Обобщенная функция Хевисайда
![]()
для которой можно записать
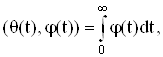
является регулярной обобщенной функцией.
2.Действия над обобщенными функциями
Введем в пространстве обобщенных функций K' операцию предельного перехода. Последовательность ![]() сходится к f, если для любого j Î K выполнено следующее соотношение
сходится к f, если для любого j Î K выполнено следующее соотношение
(fn, j) ® (f, j)
n ®¥
Определим теперь для обобщенных функций операцию дифференцирования и рассмотрим ее свойства. Производная f '(t) регулярной обобщенной функции f (t) равна
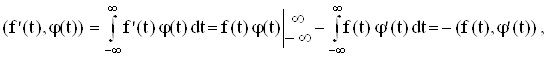
так как основная функция обращается в нуль вне некоторого конечного интервала. Производная n – го порядка будет тогда определяться равенством
(f(n) (t), j(t) = (-1)n (f (t), j(n) (t)) (" n Î N, j Î K).
Это соотношение определяет производную n – го порядка обобщенных функций, включая и сингулярные функции.
Примеры:
1. Производная функции Хевисайда равна
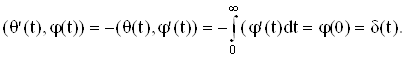
2. Так как
![]()
то
![]()
Из определения дельта – функции следует
t d(t) = 0,
а значит
d(t) + t d'(t) = 0,
2d'(t) + t d''(t) = 0,
---------------------
nd(n-1)(t) + t d(n)(t) = 0.
Отсюда последовательным исключением получаемtnd(n) (t) = (-1) n! d(t) n Î N.
Методом математической индукции можно показать, что![]()
Легко также показать, что если a(t) Î Cm, то
a(t)d(m) (t – to) = Com a (to) d(m) (t – to) - C1m a' (to) d(m-1) (t – to) –
- . . . – (-1)Cmm a(m) (to) d(t – to) .
Введем обобщенные функции t + и t -:
![]()
тогда
![]()
Можно вычислить производные
(t+)' = q(t), (t-)' = -q(-t),
а также
n ![]()
2.1 Свертка обобщенных функций
Пусть f(t) и g(t) - интегрируемые на любом конечном интервале функции. Свертка функций f(t) и g(t) определяется соотношением
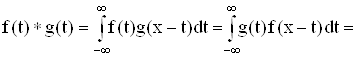
![]()
если только интеграл существует и интегрируем по любому конечному интервалу переменной х. Равенство двух интегралов легко проверить, сделав замену z = x-t.
Если f(t), g(t) – регулярные обобщенные функции и j(х) Î K, то можно записать
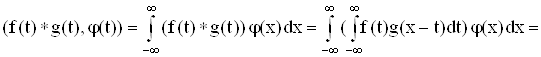
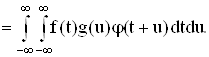
Произведение f(t) g(u) можно рассматривать как прямое произведение f(t) х g(u), так что
![]()
Это соотношение определяет свертку обощенных функций f(t), g(t) Î K', включая и сингулярные обобщенные функции.
Свертка обобщенных функций обладает следующими свойствами:
1) ![]()
2) ![]()
3) ![]()
![]()
4) если 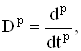 то
то
![]() (3)
(3)
Приведем доказательство последнего соотношения. Действительно, для j(х) Î K
![]()
![]()
или
![]()
![]()
![]()
что и доказывает соотношение (3).
Примеры:
1. ![]()
2. ![]()
Похожие работы
... ресурсов (т.е. масштаб производства) M=kal1-a В результате получаем , что выпуск Х есть произведение экономической эффективности и масштаба производства: Х=ЕМ. Линейная производственная функция X=F(K,L)=EKK+ELL Где EK и EL частные эффективности ресурсов. EK = -фондоотдача , EL = - производитель труда. Поскольку частные показатели эффективности имеют одинаковую размерность ...
... линейное множество, имеющее мощность континуума. Поскольку уточненное определение d -функции не затрагивает ее определения как функционала на пространстве D, все свойства d -функции, рассматриваемой как сингулярная обобщенная функция, сохраняются. Производная d -функции имеет наглядное представление в виде оси ординат, обладает двойной направленностью в каждой из полуплоскостей y<0 и y>0 и ...
... : распознавание его специфики, интерпретация и описание. В период восприятия и предварительного знакомства применяются эмпирические методы сбора информации (опрос, наблюдение, работа с документацией и др.), идут процессы распознавания особенностей педагогического опыта, его интерпретации, происходит преобразование и моделирование педагогической деятельности учителя, учебных действий учащихся, ...
... Целью формирующей работы является развитие мышление у детей шестого года жизни посредством игровых занимательных задач. Задачи: 1. Разработать систему игр и упражнений по развитию мышления у детей шестого года жизни посредством игровых занимательных задач. 2. Определить эффективные педагогические условия развития мышления у детей шестого года жизни посредством игровых занимательных задач. ...
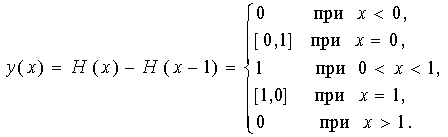

0 комментариев