Навигация
Преобразование Фурье обобщенных функций
3. Преобразование Фурье обобщенных функций
Пусть основное пространство K состоит из бесконечно дифференцируемых комплексно-значных функций j(t) действительного переменного t, равных нулю вне некоторого конечного интервала. Преобразование Фурье функции j(t) определяется соотношением
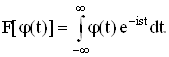
Если рассматривать s как комплексную переменную s = u + iv, то
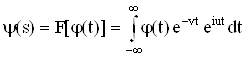
и y(t) – бесконечно дифференцируемая функция (аналитическая) во всей комплексной плоскости. Интегрируя по частям, получаем
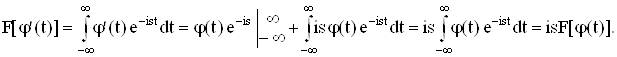
В общем случае можно записать
![]()
Далее, если 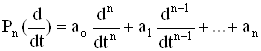 - дифференциальный полином с постоянныим коэффициентами
- дифференциальный полином с постоянныим коэффициентами ![]() то
то
![]()
Определение. Преобразование Фурье обобщенной функции f(t) называется обобщенная функция F[f(t)] = F(s), определяемая соотношением
(F[f(t)], F[j(t)]) = 2p(f(t), j(t)),
которое для регулярных функций называется равенством Парсеваля.
Свойства преобразования Фурье
1) ![]()
2) ![]()
3) F-1[F[f(t)]] = f(t), где F-1 – оператор, обратный F, удовлетворяющий соотношению ![]()
4) F[F[f(t)]] = 2pf(-t);
5) ![]()
Приведем преобразование Фурье от некоторых обобщенных функций.
F[1(t)] = 2pd(u),
![]()
F[d(t-a)] = e-iua,
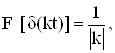
![]()
4. Преобразование Лапласа обобщенных функций
Определение. Комплекснозначная функция f(t) действительного переменного t называется оригиналом, если
1) f(t) = 0 для t < 0;
2) f(t) – кусочно дифференцируема;
3) ![]()
Тогда функция 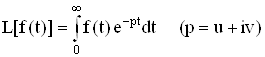 называется преобразованием Лапласа функции f(t). Функция L(p) бесконечно дифференцируема в полуплоскости Re p > a и для нее справедливо соотношение
называется преобразованием Лапласа функции f(t). Функция L(p) бесконечно дифференцируема в полуплоскости Re p > a и для нее справедливо соотношение
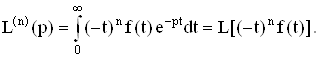
Если ![]() то
то
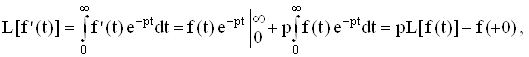
где f(+0) – скачок функции f(t) в начале координат. Обратное преобразование Лапласа L-1 равно
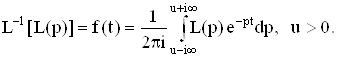
Приведем преобразование Лапласа некоторых функций:
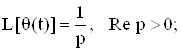
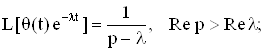
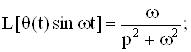
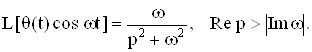
Определение. Преобразование Лапласа обобщенной функции f(t) определяется соотношением
![]()
Свойства.
1) 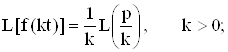
2) ![]()
3) ![]()
Здесь производные нужно рассматривать как производные обобщенных функций.
Заметим, что
![]()
![]()
![]()
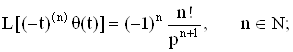
![]()
4) ![]()
тогда
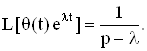
5) Найдем преобразование Лапласа свертки обобщенных функций f(t) и g(t):
![]()
![]()
Cледовательно
![]()
Так как ![]() то
то
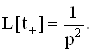
Аналогично можно написать
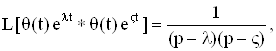
![]()
Приведем преобразование Лапласа часто используемых обобщенных функций:
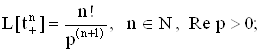
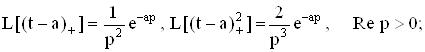
![]()
![]()
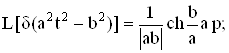
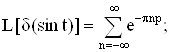
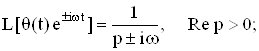
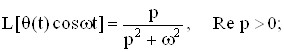
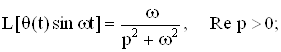
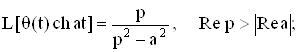
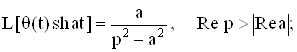
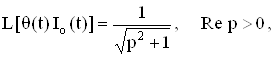
где Io - функция Бесселя нулевого порядка.
5.Дифференциальные уравнения в обобщенных функциях
Рассмотрим уравнение
![]()
Если f(t) – обычная функция, то его решением является первообразная, то есть
![]()
Пусть теперь f(t) – обобщенная функция.
Определение. Обобщенная функция g(t) называется первообразной обобщенной функцией f(t), если
(g'(t), j(t)) = (f (t), j(t)).
Если f(t) – сингулярная обобщенная функция, то возможны случаи, когда ее первообразная – регулярная обобщенная функция. Например, первообразная d(t) является y(t) = q(t); первообразная q(t) является функция y(t) = t+, а решение уравнения
y''(t) = d(t)
можно записать в виде
t(t) = t+ + C1t + C2 (C1, C2 = const).
Рассмотрим линейное уравнение n-го порядка с постоянными коэффициентами
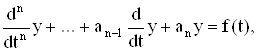 (4)
(4)
где f(t) – обобщенная функция. Обозначим

дифференциальный полином n-го порядка.
Определение. Обобщенным решением дифференциального уравнения (4) называется обобщенная функция y(t), для которой выполняется соотношение
![]()
Если f(t) – непрерывная функция, тогда единственным решением уравнения (4.) является классическое решение.
Определение. Фундаментальным решением уравнения (4) называется любая обобщенная функция e(t) такая, что
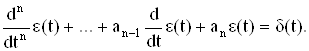
Функция Грина – фундаментальное решение, удовлетворяющее данному граничному, начальному или асимптотическому условию.
Теорема. Решение уравнения (4) существует и имеет вид
![]() (5)
(5)
если только свертка определена.
Доказательство. Действительно,
![]()
По свойству свертки имеем
![]()
В качестве примера рассмотрим уравнение
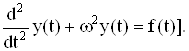 (6)
(6)
Нетрудно видеть, что фундаментальным решением этого уравнения является
![]()
так как
![]()
и
![]()
Поэтому
![]()
6. Пространство обобщенных функций ![]()
Совокупность обобщенных функций, порождаемых основным пространством K, образует пространство K'. Рассмотрим подпространство обобщенных функций ![]() пространства K, состоящее их обобщенных функций, равных нулю вне некоторого конечного интервала принадлежащего [0, ¥]. Введем в этом пространстве операцию умножения двух функций в виде свертки этих функций. Если f(t), g(t) Î
пространства K, состоящее их обобщенных функций, равных нулю вне некоторого конечного интервала принадлежащего [0, ¥]. Введем в этом пространстве операцию умножения двух функций в виде свертки этих функций. Если f(t), g(t) Î ![]() то и
то и ![]() Кроме того свертка обладает всеми свойствами обычной операции умножения. Роль единицы в
Кроме того свертка обладает всеми свойствами обычной операции умножения. Роль единицы в ![]() играет функция d(t), так как для
играет функция d(t), так как для ![]()
![]()
Пусть существует ![]() такая что
такая что
![]()
тогда f-1(t) называется обратной обобщенной функцией f(t).
Пространство ![]() с введенной операцией умножения образует алгебру (коммутативную) со сверткой.
с введенной операцией умножения образует алгебру (коммутативную) со сверткой.
Рассмотрим алгебру со сверткой ![]() . Обобщенная функция
. Обобщенная функция ![]() так как она равна нулю всюду, кроме точки ноль. Обобщенная функция
так как она равна нулю всюду, кроме точки ноль. Обобщенная функция ![]() сосредоточена вначале координат, поэтому
сосредоточена вначале координат, поэтому ![]() Далее,
Далее,
![]()
поэтому
![]()
Теорема. Пусть для ![]() существуют обратные функции f - 1(t) и g-1(t). Тогда свертка
существуют обратные функции f - 1(t) и g-1(t). Тогда свертка ![]() имеет обратную функцию вида
имеет обратную функцию вида
![]()
Действительно,
![]()
Рассмотрим следующее определенное в ![]() уравнение в свертках
уравнение в свертках
![]()
Свертка существует для любой обобщенной функции ![]() так как
так как
![]()
Следовательно, y(t) является фундаментальным решением уравнения (4). В частности, фундаментальное решение уравнения (6) с оператором 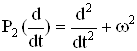 принадлежит алгебре со сверткой
принадлежит алгебре со сверткой ![]() Следовательно,
Следовательно,
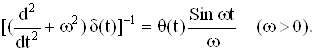
Рассмотрим операционный метод решения уравнения в свертках. Пусть имеется уравнение
![]()
где a(t) и b(t) Î![]() Среди эффективных методов решения этого уравнения приведем метод преобразования Лапласа. Применив преобразование Лапласа к левой и правой части этого уравнения, имеем
Среди эффективных методов решения этого уравнения приведем метод преобразования Лапласа. Применив преобразование Лапласа к левой и правой части этого уравнения, имеем
![]()
Отсюда следует
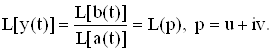
Если для функции L(p) существует оригинал, принадлежащий ![]() то он и является искомым решением.
то он и является искомым решением.
В качестве примера рассмотрим уравнение
![]()
Применив к нему преобразование Лапласа, получим (р2-w2) L[y(t)] = 1.
Следовательно,
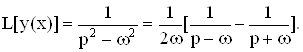
Откуда находим решение
![]()
7.Задача Коши
Рассмотрим линейное неоднородное уравнение![]() (7)
(7)
Задачей Коши для этого уравнения называется задача, заключающаяся в определении функции ![]() удовлетворяющей этому уравнению и начальным условиям в точке t = to:
удовлетворяющей этому уравнению и начальным условиям в точке t = to:
yo = y(to), y'o = y'(to), . . . , yo(n-1) = y(n-1)(to).
Задача Коши имеет единственное решение. Найдем решение, удовлетворяющее уравнению (7), а также начальным условиям.
![]() (8)
(8)
t®+0
Запишем уравнение (8) в обобщенных функциях, продолжив функцию f(t) и искомое решение нулевым значением для t<0. Введем функции
![]()
и соответствующие обобщенные функции. Начальные условия в этом случае являются скачками функции y(t) и ее производных до n-1-го порядка включительно в точке t = 0. Действительно, рассмотрим вначале случай, когда у функции y(t) только скачок yo, тогда
![]()
где y'(t) – производная в обычном смысле.
Если у функции еще и скачок производной равный y'o, то
![]()
Производную порядка p (p £ n-1) обобщенной функции ![]() можно записать в виде
можно записать в виде
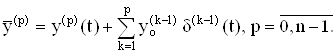
Введем обозначение
![]()
Где
![]()
Таким образом, дифференциальное уравнение (7) переходит в уравнение
![]() (9)
(9)
Преимущество этого уравнения состоит в том, что оно содержит начальные условия Коши и в формулировке задачи участвуют обобщенные функции.
Уравнение в свертках, соответствующее уравнению (9), имеет вид
![]()
Если e(t) – его фундаментальное решение, то с учетом последней формулы можно записать
![]() (10)
(10)
С помощью вариации постоянных можно записать фундаментальное решение в виде
e(t) = q(t) yn(t) ,
где yn(t) - решение однородного уравнения
![]()
с начальными условиями
![]()
Тогда решение уравнения (10) принимает вид
![]()
Таким образом, решение уравнения (7) с начальным условием (8) принимает вид
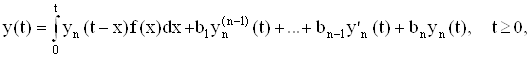
где предполагается, что f(t) – локально интегрируемая функция.
Пример. Рассмотрим уравнение
y''(t) = 0, t ³ 0
с начальными условиями
lim y(t) = yo , lim y'(t) = y'o
t®+0 t®+0
В этом уравнении а1 = а2 = 0 и b1 = yo, b2 = y'o, а функция y2(t) = t является решением однородного уравнения, удовлетворяющая условиям
y2(0) = 0 , y'(0) = 1.
Поэтому
y(t) = yo + y'o t , t ³ 0.
Можно также написать
![]()
Похожие работы
... ресурсов (т.е. масштаб производства) M=kal1-a В результате получаем , что выпуск Х есть произведение экономической эффективности и масштаба производства: Х=ЕМ. Линейная производственная функция X=F(K,L)=EKK+ELL Где EK и EL частные эффективности ресурсов. EK = -фондоотдача , EL = - производитель труда. Поскольку частные показатели эффективности имеют одинаковую размерность ...
... линейное множество, имеющее мощность континуума. Поскольку уточненное определение d -функции не затрагивает ее определения как функционала на пространстве D, все свойства d -функции, рассматриваемой как сингулярная обобщенная функция, сохраняются. Производная d -функции имеет наглядное представление в виде оси ординат, обладает двойной направленностью в каждой из полуплоскостей y<0 и y>0 и ...
... : распознавание его специфики, интерпретация и описание. В период восприятия и предварительного знакомства применяются эмпирические методы сбора информации (опрос, наблюдение, работа с документацией и др.), идут процессы распознавания особенностей педагогического опыта, его интерпретации, происходит преобразование и моделирование педагогической деятельности учителя, учебных действий учащихся, ...
... Целью формирующей работы является развитие мышление у детей шестого года жизни посредством игровых занимательных задач. Задачи: 1. Разработать систему игр и упражнений по развитию мышления у детей шестого года жизни посредством игровых занимательных задач. 2. Определить эффективные педагогические условия развития мышления у детей шестого года жизни посредством игровых занимательных задач. ...
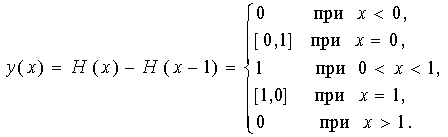

0 комментариев