Исследование частоты встречаемости антипростых чисел среди натуральных чисел

1.3 Исследование частоты встречаемости антипростых чисел среди натуральных чисел

Будем исследовать частоту встречаемости антипростых чисел среди натуральных чисел в следующем смысле. Необходимо исследовать свойства частоты встречаемости антипростых чисел на отрезках длины т, расположенных в ряду натуральных чисел от 1 до 1000000 и др. и получить какие-либо общие закономерности. Назовем частотой встречаемости антипростых чисел на отрезке [1, т] число t(т) = p(т)/т. Аналогично t(k, т) = p(k, т)/(т – k +1) – частота встречаемости антипростых чисел на отрезке [k, т]. Для оценки частоты встречаемости антипростых чисел на отрезке от 1 до m построим графики функций t(т) = p(т)/т (см рис. 4).

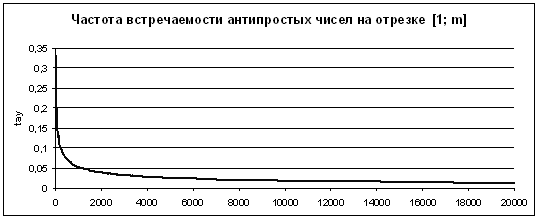
Рисунок 4 – График функции

Изучив график частоты t(т) = p(т)/т встречаемости антипростых чисел на отрезке от 1 до m, получим, что при малых значениях m он колеблется, то возрастая, то убывая (максимумы при антипростых m), но достигнув своего наибольшего значения  при m = 9 приобретает тенденцию к убыванию.

На рисунке 5 представлен графики функций t(т) и y(x)= () для .

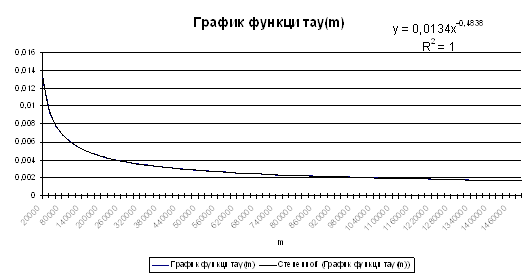
Рисунок 5 - График функции t(т) и y(x)=

Из графика на рис. 5 и из предыдущего пункта при больших m получаем гипотезу t(т).

В таблице 2 (см Приложение Г) приведено сравнение значений функций t(m), f(m)= и y(x)= до m= 1500000 и вычислена средняя ошибка приближения.

Средняя ошибка приближения функции t(m) к функции f(m)= составила 1,185812%, а к функции y(x)= – 0,280031%.

Исследование функции t(k, т) = p(k, т)/(т – k +1) – частоты встречаемости антипростых чисел на отрезке [k, т], не позволило выявить закономерностей. Ясно лишь, что она при любом m принимает значения от 0 до 1. Всего различных значений не более m+1, а при m > 3 не более m и среди них будет 1. Есть гипотеза (строго это не доказано), что t(k, т) не периодическая функция. Это также будет следовать из доказанной ниже теоремы 5.

2 Обобщения об антипростых числах

Цель данной работы не только решить поставленные на турнире задачи, но и предложить свои вопросы для исследования задачи об антипростых числах и исследовать их.

Докажем ряд теорем, которые могут представлять интерес при исследовании антипростых чисел.

Теорема 1. Любое нечетное число можно представить как разность двух антипростых чисел.

Доказательство:

Заметим, что 1 = 9 – 8 и 3 = 128 – 125. Пусть теперь 2p + 1 – произвольное нечетное число и p > 1. Тогда числа p² и (p + 1)² – антипростые. Их разность, как легко заметить, равна 2p + 1.

Теорема 2. Любое натуральное число, делящееся на 4, можно представить как разность двух антипростых чисел.

Доказательство: Заметим, что 4 = 8 – 4 и 8 = 16 – 8. Пусть теперь 4p – произвольное число, делящееся на 4 и p > 2. Тогда числа (p – 1)² и (p + 1)² – антипростые. Их разность, как легко заметить, равна 4p.

Теорема 3 . Существует отрезок любой длины в натуральном ряду, на котором нет антипростых чисел.

Доказательство: Рассмотрим систему сравнений:

( –простые числа и ).

Если данная система имеет решения, то тогда получим последовательность чисел длины  такую, что каждый её член делится на (), но не делится на , то есть не является антипростым числом. Но данная система имеет решения по Китайской теореме об остатках (числа  попарно взаимно простые).

Значит существует отрезок любой длины в натуральном ряду, на котором нет антипростых чисел.

Примечание. Китайская теорема об остатках[6].

Если  – попарно взаимно простые числа,  – такие числа, что , то существует такое число , что  при всех .

Также нам понадобиться следующий известный факт:

Лемма. Пусть НОД(b;d) = 1. Тогда найдется бесконечно много членов арифметической (геометрической) прогрессии с начальным членом 1 и разностью (знаменателем) b сравнимых с 1 по модулю d.

Теорема 4. В любой арифметической прогрессии (a₀,d Î N, a₀ > 0), у которой НОД(a₀;d) – антипростое или 1, бесконечно много антипростых чисел.

Доказательство:

Пусть НОД(a₀;d) = 1. Рассмотрим арифметическую прогрессию с членами вида a₀ + a₀kd. Каждый ее член является членом исходной арифметической прогрессии. При 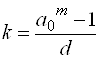 члены этой прогрессии антипростые числа. Но согласно лемме, найдется бесконечно много таких k. Следовательно, прогрессия содержит бесконечно много антипростых чисел.

В случае, когда НОД(a₀;d) – антипростое, рассуждения аналогичны.

Теорема 5. Не существует арифметической прогрессии (,) состоящей только из антипростых чисел или такой у которой после n-ого члена все члены – антипростые числа.

Доказательство:

Если все члены арифметической прогрессии (разность , ) после -ого члена () – антипростые числа, то взяв арифметическую прогрессию с  и разностью , получим арифметическую прогрессию, состоящую только из антипростых чисел.

Пусть существует арифметическая прогрессия, состоящая только из антипростых чисел ().

Рассмотрим , и простое число .

Если  представимо в виде (то есть сравнение  имеет решение), то тогда  не антипростое число (делится на , но не делится на ).

Но сравнение имеет решение согласно лемме, так как НОД()=1. Значит  не антипростое число – противоречие.

Значит не существует арифметической прогрессии, состоящей только из антипростых чисел.

Следствие. В любой арифметической прогрессии(,) бесконечно много не антипростых чисел (если , то и ).

Одно из примечательных в теории чисел понятий – совершенное число. Это натуральное число, равное сумме своих натуральных делителей, исключая само число. На октябрь 2008 г. известно только 46 чётных совершенных чисел, нечетных совершенных чисел найдено не было. Встает вопрос, а могут ли антипростые числа быть совершенными? В этой связи интересны следующие две теоремы.

Теорема 6. Число вида  не совершенно ( – простое, – натуральное).

Действительно, если  – совершенно, то верно следующее:

Следовательно  – не совершенно.

Теорема 7. Число вида  не совершенно (– целое).

Доказательство:

Пусть  совершенно. Рассмотрим два случая:

1. – чётно. Представим  в виде произведения простых множителей:

. Количество натуральных делителей числа  равно , притом количество чётных  их сумма чётна, нечётных  их сумма нечётна, сумма всех натуральных делителей  – нечётна, но их сумма равна – противоречие.

2. – нечётно. Представим  в виде произведения простых множителей:

. Количество натуральных делителей числа  равно , сумма их нечётна, но она же равна – противоречие.

Сложным оказался вопрос о существовании трёх подряд идущих антипростых числах, пытаясь его ослабить, мы попытались рассмотреть совместное расположение последовательно расположенных простых и антипростых чисел. При этом нами был поставлен ряд вопросов, на которые удалось получить ответы.

Вопрос 1. Существуют ли три подряд идущих натуральных числа, каждое из которых является либо простым, либо антипростым?

Ответ. Рассмотрим тройки вида (p₁; p₂; a) (a; p₁; p₂): Одно из чисел p₁ или p₂ чётное, то есть 2, так как 1 не антипростое и не простое, то троек (a; p₁; p₂) нет. А тройка (p₁; p₂; a) всего одна (2;3;4).

Рассмотрим тройки вида ().  – нечётные (иначе одно не анипростое по задачи 1 пункта 1.1), тогда  – чётно, то есть 2, но 1 не антипростое, то есть данной тройки не существует.

Очевидно, что тройки (p₁; p₂; p₃ ) не существует.

Тройки (p; a₁; a₂), (p₁; a; p₂), () существуют: (7; 8; 9), (3; 4; 5), (675;676;677) но доказать их конечность или бесконечность не удалось.

Примечание. В приведенных обозначениях p – простое число, a – антипростое число.

Вопрос 2. Существуют ли четыре подряд идущих натуральных числа, каждое из которых является либо простым, либо антипростым?

Ответ. Среди четырёх подряд идущих натуральных чисел два чётных, но из задачи 1 пункта 1.1, следует что они одновременно не могут быть антипростыми, также как и простыми. Значит, если существует четвёрка, то одно из них простое. Так как 1 не антипростое, то имеем только одну четвёрку: (2;3;4;5).

Вопрос 3. Существуют ли пять или более подряд идущих натуральных чисел, каждое из которых является либо простым, либо антипростым?

Ответ. Как показано выше, существует только одна четверка подряд идущих натуральных числа, каждое из которых является либо простым, либо антипростым. Если бы существовало пять или более подряд идущих натуральных чисел, удовлетворяющих условию, то они содержали бы эти четыре числа. Но 6 и 1 не простое и не антипростое. Значит, таких чисел нет.

Заключение

В процессе выполнения данной работы были решены задачи, предлагаемые на XI турнире юных математиков, и получены следующие результаты.

Для исследования антипростых чисел была разработана программа на Паскале, которая вычисляет антипростые числа. В Приложении А представлена таблица антипростых чисел на отрезке до . В принципе программа позволяет повысить значение n до большей величины, а также дает ответ, что среди чисел на отрезке до