Троек антипростых чисел вида n - 1, n, n + 1 не найдено

3136000000 троек антипростых чисел вида n - 1, n, n + 1 не найдено.

При исследовании количества антипростых чисел были проведены сравнения значений функции p(n) с функцией, которые показали, на отрезке до n=420000   p(n), а далее   p(n), причём процент ошибки небольшой. Так как вначале   p(n), то процент ошибки убывает, после n=420000 он начинает возрастать, и при n=2000000 он приблизительно равен 2%.

При исследовании частоты встречаемости антипростых чисел среди натуральных чисел были проведены сравнения значений функции t(m) с функцией f(m)= и t(m) с полученной функцией y(x)= () до m= 1500000. Вычислена средняя ошибка приближения. Средняя ошибка приближения функции t(m) к функции f(m)= составила 1,185812%, а к функции y(x)= - 0,280031%.

В обобщениях об антипростых числах были сформулированы и доказаны семь теорем, а также три вопроса.

В заключении следует отметить, что тематика данной исследовательской работы является достаточно новой и поэтому и достаточно интересной.

В дальнейшем планирую продолжать исследовать антипростые числа.

Список использованных источников и литературы

1.  Сендеров В., Френкин Б. Гипотеза Каталана. - журнал "Квант", 2007, №4. – С. 8-10.

2.  Сендеров В. Решение задачи М2032. – журнал Квант", 2007, №4. – С. 19-21.

3.  Оре О. Приглашение в теорию чисел – Серия "Библиотечка "Квант"", М. 1980. – 128 с.

4.  Виноградов И.М. Основы теории чисел. – М.: Наука, 1972. – 168 с.

5.  Нестеренко Ю.В. Теория чисел. – М.: Академия, 2008. -273 с.

6.  Манин Ю.И., Панчишкин А.А. Теория чисел I. Введение в теорию чисел. – М.: ВИНИТИ, 1989.- 402 с.

Приложение A - +Таблица антипростых чисел

Приложение Б – Программа нахождения антипростых чисел

program Project2;

var

k:real;

b,t,i,j,m,n:longint;

a:array[1..2000000] of longint;

begin

assign(output,'output.txt');

rewrite(output);

m:=3;

a[1]:=2;

a[2]:=3;

for i:=4 to 2000000 do begin

t:=1;

k:=sqrt(i);

b:=trunc(k);

for j:=2 to b do

if(i mod j)=0 then

t:=t+1;

if t=1 then begin

a[m]:=i;

m:=m+1;

end;

end;

n:=1;

for i:=1 to 2000000 do begin

t:=1;

for j:=1 to m-1 do

if(i mod a[j])=0 then begin

b:=i div a[j];

if (b mod a[j])=0 then

t:=t+1

else

begin

t:=1;

break;

end;

end;

if t>1 then

begin

writeln(i);

end;

end;

readln;

close(output);

end.

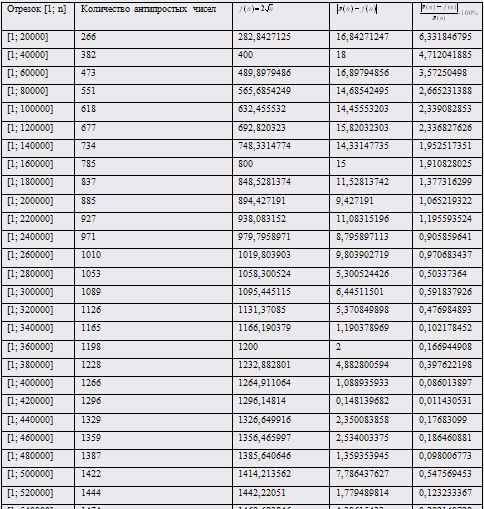
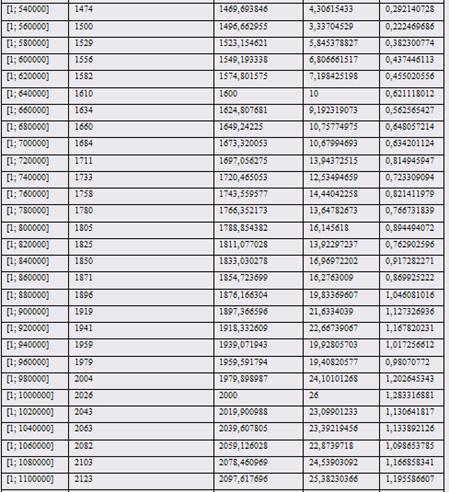
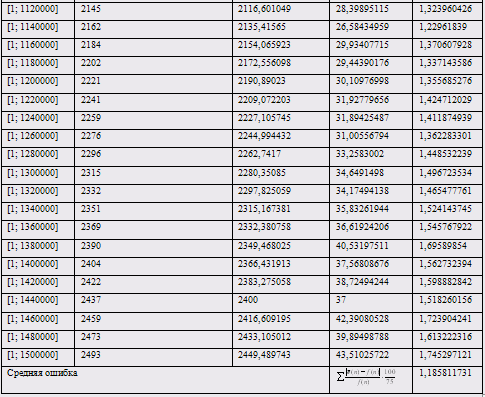
Приложение В – Таблица сравнения значений функций p(n) и

 

Таблица 1 – Сравнение значений функций p(n) и

Приложение Г – Таблица сравнения значений функций t(m), f(m)= и y(x)=

Таблица 2 – Сравнение значений функций t(m), f(m)= и y(x)=

Отрезок [1; m]	Количество антипростых чисел p(n)	Значение функции t(m)	Значение функции f(m)=	Значение функции y(x)=
[1; 20000]	266	0,0133	0,014142	0,0134	6,331847	0,75188
[1; 40000]	382	0,00955	0,01	0,009582228	4,712042	0,337463
[1; 60000]	473	0,007883	0,008165	0,007875417	3,572505	0,100424
[1; 80000]	551	0,006888	0,007071	0,006852171	2,665231	0,512948
[1; 100000]	618	0,00618	0,006325	0,006150963	2,339083	0,469855
[1; 120000]	677	0,005642	0,005774	0,005631644	2,336828	0,177647
[1; 140000]	734	0,005243	0,005345	0,005226926	1,952517	0,30386
[1; 160000]	785	0,004906	0,005	0,00489993	1,910828	0,128818
[1; 180000]	837	0,00465	0,004714	0,004628521	1,377316	0,461906
[1; 200000]	885	0,004425	0,004472	0,004398502	1,065219	0,598824
[1; 220000]	927	0,004214	0,004264	0,004200287	1,195594	0,316802
[1; 240000]	971	0,004046	0,004082	0,004027142	0,90586	0,461997
[1; 260000]	1010	0,003885	0,003922	0,003874173	0,970683	0,268815
[1; 280000]	1053	0,003761	0,00378	0,003737731	0,503374	0,611139
[1; 300000]	1089	0,00363	0,003651	0,00361503	0,591838	0,41241
[1; 320000]	1126	0,003519	0,003536	0,003503899	0,476985	0,42206
[1; 340000]	1165	0,003426	0,00343	0,003402621	0,102178	0,696032
[1; 360000]	1198	0,003328	0,003333	0,003309817	0,166945	0,539728
[1; 380000]	1228	0,003232	0,003244	0,003224362	0,397622	0,223323
[1; 400000]	1266	0,003165	0,003162	0,003145332	0,086014	0,621423
[1; 420000]	1296	0,003086	0,003086	0,003071957	0,011431	0,445845
[1; 440000]	1329	0,00302	0,003015	0,00300359	0,176831	0,558332
[1; 460000]	1359	0,002954	0,002949	0,002939686	0,186461	0,496296
[1; 480000]	1387	0,00289	0,002887	0,002879775	0,098007	0,339428
[1; 500000]	1422	0,002844	0,002828	0,002823459	0,547569	0,722272
[1; 520000]	1444	0,002777	0,002774	0,002770389	0,123233	0,235313
[1; 540000]	1474	0,00273	0,002722	0,002720264	0,292141	0,34312
[1; 560000]	1500	0,002679	0,002673	0,00267282	0,22247	0,214713
[1; 580000]	1529	0,002636	0,002626	0,002627826	0,382301	0,317905
[1; 600000]	1556	0,002593	0,002582	0,002585077	0,437446	0,318356
[1; 620000]	1582	0,002552	0,00254	0,002544392	0,455021	0,282996
[1; 640000]	1610	0,002516	0,0025	0,002505609	0,621118	0,398166
[1; 660000]	1634	0,002476	0,002462	0,002468583	0,562565	0,289788
[1; 680000]	1660	0,002441	0,002425	0,002433186	0,648057	0,327323
[1; 700000]	1684	0,002406	0,00239	0,002399301	0,634201	0,266598
[1; 720000]	1711	0,002376	0,002357	0,002366822	0,814946	0,402569
[1; 740000]	1733	0,002342	0,002325	0,002335656	0,723309	0,266293
[1; 760000]	1758	0,002313	0,002294	0,002305714	0,821412	0,321793
[1; 780000]	1780	0,002282	0,002265	0,00227692	0,766732	0,224861
[1; 800000]	1805	0,002256	0,002236	0,002249201	0,894494	0,312442
[1; 820000]	1825	0,002226	0,002209	0,002222491	0,762903	0,14014
[1; 840000]	1850	0,002202	0,002182	0,002196731	0,917282	0,256558
[1; 860000]	1871	0,002176	0,002157	0,002171865	0,869925	0,170839
[1; 880000]	1896	0,002155	0,002132	0,002147842	1,046081	0,311116
[1; 900000]	1919	0,002132	0,002108	0,002124617	1,127327	0,356696
[1; 920000]	1941	0,00211	0,002085	0,002102144	1,16782	0,362034
[1; 940000]	1959	0,002084	0,002063	0,002080386	1,017257	0,17547
[1; 960000]	1979	0,002061	0,002041	0,002059303	0,980708	0,104546
[1; 980000]	2004	0,002045	0,00202	0,002038862	1,202645	0,295148
[1; 1000000]	2026	0,002026	0,002	0,002019032	1,283317	0,34395
[1; 1020000]	2043	0,002003	0,00198	0,001999781	1,130642	0,157798
[1; 1040000]	2063	0,001984	0,001961	0,001981082	1,133892	0,129668
[1; 1060000]	2082	0,001964	0,001943	0,001962909	1,098654	0,063238
[1; 1080000]	2103	0,001947	0,001925	0,001945238	1,166858	0,101911
[1; 1100000]	2123	0,00193	0,001907	0,001928046	1,195587	0,101258
[1; 1120000]	2145	0,001915	0,00189	0,001911311	1,32396	0,201927
[1; 1140000]	2162	0,001896	0,001873	0,001895015	1,229618	0,077865
[1; 1160000]	2184	0,001883	0,001857	0,001879137	1,370608	0,192382
[1; 1180000]	2202	0,001866	0,001841	0,00186366	1,337144	0,130865
[1; 1200000]	2221	0,001851	0,001826	0,001848567	1,355685	0,122443
[1; 1220000]	2241	0,001837	0,001811	0,001833843	1,424712	0,165603
[1; 1240000]	2259	0,001822	0,001796	0,001819473	1,411875	0,126297
[1; 1260000]	2276	0,001806	0,001782	0,001805443	1,362283	0,050154
[1; 1280000]	2296	0,001794	0,001768	0,00179174	1,448532	0,11207
[1; 1300000]	2315	0,001781	0,001754	0,00177835	1,496724	0,135835
[1; 1320000]	2332	0,001767	0,001741	0,001765263	1,465478	0,079447
[1; 1340000]	2351	0,001754	0,001728	0,001752467	1,524144	0,114608
[1; 1360000]	2369	0,001742	0,001715	0,001739951	1,545768	0,112571
[1; 1380000]	2390	0,001732	0,001703	0,001727705	1,695899	0,241297
[1; 1400000]	2404	0,001717	0,00169	0,00171572	1,562732	0,082873
[1; 1420000]	2422	0,001706	0,001678	0,001703986	1,598883	0,096612
[1; 1440000]	2437	0,001692	0,001667	0,001692495	1,51826	0,007898
[1; 1460000]	2459	0,001684	0,001655	0,001681238	1,723904	0,17863
[1; 1480000]	2473	0,001671	0,001644	0,001670208	1,613222	0,044179
[1; 1500000]	2493	0,001662	0,001633	0,001659396	1,745297	0,156651
Средняя ошибка					1,185812
Средняя ошибка						0,280031