Элементы комбинаторики

 

 

 

 

 

 

 

 

 

 

 

 

 

Факультативный курс по теме:

Элементы комбинаторики

 

 

Автор: Лузина Татьяна Юрьевна

Рецензент: Янкина Лидия Григорьевна

Кунгурское педагогическое училище 2009 год

 

Введение

 

В данной разработке факультативного курса предлагается 11 уроков. На которых предлагается решение задач, подготовка сообщений и докладов и их защита; практические, самостоятельные работы; практикумы по решению задач, по составлению задач; контрольная работа.

Данный факультативный курс предназначен для учеников 8 класса, но может и использоваться учениками других классов, т. к. материал излагается с самих азов. Он прост, понятен и в то же время не потерял своей научности.

Оглавление

 

Предисловие

Урок 1 Введение

Урок 2 Поиск закономерностей

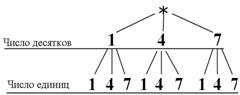
Урок 3 Перебор возможных вариантов

Урок 4 Правило суммы и правило произведения

Урок 5 Самостоятельная работа по темам: «Поиск закономерностей», «Дерево возможных вариантов», «Правило произведения»

Урок 6 Размещения

Урок 7 Тест по темам: «Размещение без повторений», «Размещение с повторениями»

Урок 8 Перестановки

Урок 9 Сочетания

Урок 10 Урок-практикум. Подготовка к контрольной работе

Урок 11 Контрольная работа

Литература

 

Предисловие

 

Вы начинаете изучать раздел математики под названием «Комбинаторика».

В данном факультативном курсе вы найдете много интересных и полезных для себя сведений, которые связаны с жизнью.

Любую тему вам поможет отыскать «Оглавление».

Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций можно составить из заданных объектов, называется комбинаторикой.

Комбинаторика возникла в XVII веке. Тогда широко были распространены лотереи, игры в карты и кости. И первые комбинаторные задачи касались именно азартных игр, так как возникало много вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре.

Основа хорошего понимания комбинаторики – умение считать, думать, рассуждать, находить удачные решения задач. Все эти навыки и способности вы можете выработать, если будете настойчивы, трудолюбивы и внимательны на уроках, будете самостоятельно и с интересом заниматься.

В данном факультативном курсе будут использованы такие виды деятельности, как практические, самостоятельные работы, решение задач, защита докладов и сообщений. Данный курс вам поможет по-другому посмотреть на окружающий мир. Изучив его, вы сможете объективно оценивать некоторые вещи, опираясь на математические подсчеты.

Желаю вам успехов в овладении тайнами удивительного раздела математики – комбинаторики!

Урок 1. Введение

 

Цели:

·  дать понятие науки «Комбинаторика», «Комбинаторные задачи»;

·  познакомить учащихся с историей данной науки;

·  привести примеры нескольких комбинаторных задач с решениями для привития интереса учащихся к данной науке.

Ход урока

1.  Сообщение темы и целей

2.  Работа по теме

Комбинаторика – ветвь математики, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов. Комбинаторика возникла в XII веке. Долгое время она лежала вне основного русла развития математики.

С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов – во время работы.

Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника.

Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных.

Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д.

Задачи, в которых идет речь о тех или иных комбинациях объектов, называются комбинаторными. Область математики, в которой изучаются комбинаторные задачи, называется комбинаторикой. Комбинаторику можно рассматривать как часть теории множеств – любую комбинаторную задачу можно свести к задаче о конечных множествах и их отображениях

Раздел комбинаторики, в котором рассматривается лишь вопрос о подсчете числа решений комбинаторной задачи, теорией перечислений.

Комбинаторика как наука стала развиваться в XIII веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н. Тарталье (1499-1557), Г. Галилею (1564-1642) и французским ученым Б. Паскалю (1623-1662) и П. Ферма. Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666 году. Он также впервые ввел термин «комбинаторика». Значительный вклад в развитие комбинаторики внес Л.Эйлер.

3.  Перечень тем докладов

1) Дж. Кардано

2) Н. Тарталье

3) Бином Ньютона

4) Б. Паскаль

5) П. Ферма

6) Треугольник Паскаля

7) Л.Эйлер

8) Г. Галилею

9) Г. Лейбниц

10) Некоторые свойства числа сочетаний

11) Правила решения комбинаторных задач

12) Комбинаторная геометрия

13) Историческая справка о науке «Комбинаторике»

14) Магические квадраты

4. Итог урока

Урок 2. Поиск закономерностей

 

Цели:

·  рассмотреть некоторые виды закономерностей.

Оборудование: мультимедийный проектор, жетоны.

Ход урока

1.  Сообщение темы и целей.

2.  Домашнее задание.

1. Выявить закономерности и записать еще 4 числа:

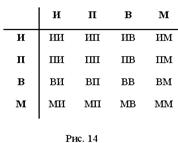
1)

562	(26)	652
369	(__)	963

2) ответ: 36 – сумма цифр в числе