Навигация
Нечетные цифры: 1, 3, 5, 7, 9
7. нечетные цифры: 1, 3, 5, 7, 9
![]()
8. ![]()
9. Рn=n!=4!=24
10. ![]()
11. 6 способов
12. ![]()
13. ![]()
14. Рn=6!=720
15. ![]()
16. Pn=5!=120
17. ![]()
18. ![]()
Урок 11: Контрольная работа по теме «Комбинаторные задачи»
Цели:
· Проверить знания, умения, навыки по всему курсу с помощью контрольной работы с разноуровневыми заданиями;
Оборудование: карточки с заданиями.
Ход урока
1. Сообщение темы и целей
2. Контрольная работа по вариантам
I вариант
Заполнить пропуски:
1. Задачи, в которых идет речь о тех или иных комбинациях объектов, называются (комбинаторными).
2. Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить способами. (m∙п)
3. Произведение всех чисел от 1 до n называется (факториалом)
4. Число размещений с повторениями находится по формуле: (![]() )
)
5. Сочетаниями … из n элементов по т элементов называются соединения, каждое из которых состоит из m элементов, взятых из данных n элементов. (без повторений)
6. Формула числа сочетаний из m элементов по n элементов с повторениями имеет вид: … (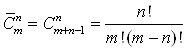 )
)
Решить задачи:
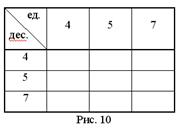
1. Сколько всевозможных двузначных чисел можно записать, используя цифры 7, 4, 5?
2. Сколькими способами можно из 6 человек составить комиссию, состоящую из двух человек?
3. В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?
4. Сколькими способами можно расставить на полке 4 различные книги?
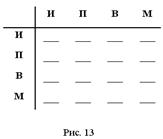
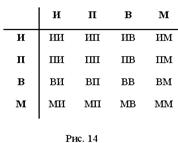
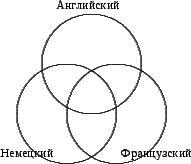
5. Сколько различных словарей необходимо переводчику, чтобы он мог переводить с любого из 5 языков – русского, английского, немецкого, французского, испанского – на любой другой из этих языков?
6. Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?
7. На плоскости отмечены 6 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?
II вариант
Заполнить пропуски:
1. Задачи, в которых идет речь о тех или иных комбинациях объектов, называются (комбинаторными).
2. Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить способами. (m∙п)
3. Произведение всех чисел от 1 до n называется (факториалом)
4. Число размещений с повторениями находится по формуле: (![]() )
)
5. Сочетаниями … из n элементов по т элементов называются соединения, каждое из которых состоит из m элементов, взятых из данных n элементов. (без повторений)
6. Формула числа сочетаний из m элементов по n элементов с повторениями имеет вид: (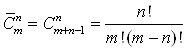 )
)
Решить задачи:
1. Сколько всевозможных двузначных чисел можно записать, используя цифры 1, 2, 3, 4, так, чтобы цифры в записи числа не повторялись?
2. Сколькими способами можно переставить 5 различных геометрических фигур?
3. Пять человек пожали друг другу руки. Сколько было рукопожатий?
4. За свои рисунки ученик получил две положительные оценки. Какими они могут быть? Сколько вариантов?
5. Сколько флагов можно составить из трех разных цветов, если имеются полосы синего, белого, красного цветов?
6. В понедельник в пятом классе 5 уроков. Сколькими способами можно составить расписание на понедельник?
7. Из десяти учащихся надо выбрать старосту, физорга и культорга. Сколькими способами это можно сделать?
Ответы и решения
| I вариант | II вариант |
| 1. 2. 3. 4. Pn=4!=24 5. Pn=5!=120 6. Pn=5!=120 7. | 1. 2. Pn=5!=120 3. 4. положительные оценки: 4, 5. 22=4 5. Рn=3!=6 6. Pn=5!=120 7. |
Литература
1. Гнеденко Б. В., Журбенко, И. Г. Теория вероятностей и комбинаторика //Математика в школе. – 2007. - №6. – с. 67-70.
2. Гусев В. А. Внеклассная работа по математике в 5-8 классах. /Под. ред. С. И. Шварцбурга. - М.: Просвещение, 1977. – 288с.
3. Дихтярь М., Эргле Е. Исторические комбинаторные задачи и комбинаторные модели //Математика. – 2007. - №14. – с. 23-24.
4. Математика: Учебник для 5 кл. общеобразоват. учреждений / Г. В. Дорофеев, С. Б. Суворова, И. Ф. Шарыгин и др.; под ред. Г. В. Дорофеева, И. Ф. Шарыгина. – 8-е изд. - М.: Просвещение, 2006. – 302с.
5. Нурк Э. Р., Тельгман А. Э. Математика: Учеб. для 5 кл. сред. шк. – 4-е изд., дораб. – М.: Просвещение, 1994. – 304с.
6. Овсянникова Л.В. Факультативный курс по математике //Начальная школа. – 2005. - №9. – с. 29-33.
7. Виленкин Н. Я. Комбинаторика. – М.: Наука, 1969. – 328с.
8. Перельман Я. И. Занимательные задачи и опыты. - Д.: ВАП, 1994. – 527с.
9. Семеновых А. Комбинаторика //Математика. – 2004. - №15. – с. 28-32.
10. Семеновых А. Комбинаторика //Математика. – 2004. - №16. – с. 19-22.
11. Семеновых А. Комбинаторика //Математика. – 2004. - №17. – с. 22-27
12. Стойлова Л. П. Математика: Учебник для студентов отделений и факультетов начальных классов средних и высших педагогических учебных заведений. - М.: Издательский центр «Академия», 1997. – 464с.
13. Цыганов Ш. Комбинаторика от А до Я //Математика. – 2001. - №26. – с. 9-23.
14. http://combinatorica.narod.ru/second.htm
Похожие работы
... обучения, школа предоставляет учащимся право выбора предметов по интересам и склонностям. В соответствии с требованиями была разработана программа факультативного курса по теме «Элементы комбинаторики» для 8 класса. 2.2 Программа факультативного курса Пояснительная записка В математике и ее приложениях часто приходится иметь дело с различного рода множествами и подмножествами: ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... уметь приобретать, обрабатывать и эффективно применять информацию. В ходе выполнения контрольной работы были изучены логические основы работы ЭВМ, основные понятия и операции алгебры логики, а также прикладного программного обеспечения. В настоящее время термин «информация» является одним из самых распространенных. Для переработки информационных ресурсов применяют специальные технологии - ...
... игрок делает выбор из 28 костей. Второй из 28-7=21 костей, третий 14, а четвертый игрок забирает оставшиеся кости. Следовательно, возможно . Размещения и сочетания с повторениями Часто в задачах по комбинаторике встречаются множества, в которых какие-либо компоненты повторяются. Например: в задачах на числа – цифры. Для таких задач при размещениях используется формула , а для сочетаний . Примеры ...




0 комментариев