Навигация
6. Расчет зубчатых передач
6.1 Определение межосевого расстояния
Межосевое расстояние определяется по формуле:
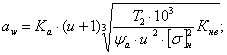
где а) Ка -вспомогательный коэффициент. Для косозубых передач Ка = 43. для прямозубых- Ка = 49.5;
б) ψа=b2/aw - коэффициент ширины венца колеса, равный 0,28...0,36 -для шестерни, расположенной симметрично относительно опор в проектируемых нестандартных одноступенчатых цилиндрических редукторах; ψа = 0,2...0,25 - для шестерни, консольно расположенной относительно опор в открытых передачах;
в) u - передаточное число редуктора или открытой передачи
г) Т2 - вращающий момент на тихоходом валу редуктора
д) [σ]н - допускаемое контактное напряжение колеса с менее прочным зубом или среднее допускаемое контактное напряжение. Н/мм2;
е) Кнв - коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев Кнв.
Полученное значение межосевого расстояния aw для нестандартных передач округлить до ближайшего значения из ряда нормальных линейных размеров.
Определим значение межосевого расстояния первой ступени.
Поскольку первая передача шевронная раздвоенная то в данном случае Т2=Твх/2=1052/2=526Нм
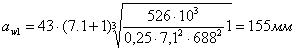
Определим значение межосевого расстояния второй ступени

Определим значение межосевого расстояния третей ступени
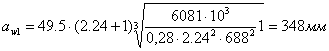
6.2 Определение модуля зацепления
Модуль зацепления определяется по формуле:
![]() , мм
, мм
где Кт – вспомогательный коэффициент, для прямозубых передач Кт=6,8, для косозубых Кт=5,3;
d2=2awu/(u+1) – делительный диаметр колеса, мм;
b2=ψ∙aw– ширина венца. мм;
[σ]f- допускаемое напряжение изгиба материала колеса с менее прочным зубом.
В итоге получаем:
- первая ступень:
d2=2∙155∙7,1/(7,1+1)=272мм
b2=0,25∙155=39мм
![]()
Выбираем значения модуля из стандартного ряда m=1.75мм
-вторая ступень:
d2=2∙237∙2.8/(2.8+1)=350мм
b2=0,28∙237=66.4мм
![]()
Выбираем значения модуля из стандартного ряда m=4.5мм
-третья ступень:
d2=2∙348∙2.24/(2.24+1)=401мм
b2=0,28∙348=97.4мм
![]()
Выбираем значения модуля из стандартного ряда m=7мм
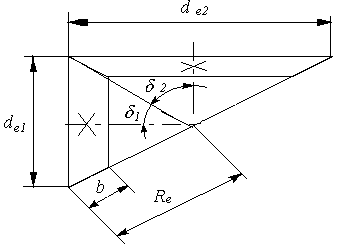
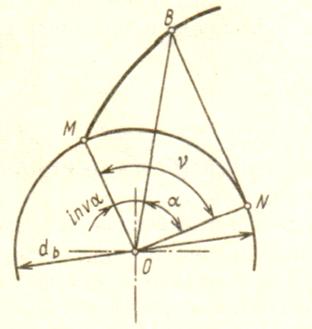
6.3 Определение угла наклона зубьев
Угол наклона зубьев определяется по формуле:
![]()
Определим угол наклона зубьев первой ступени:
![]()
Определим угол наклона зубьев второй ступени:
![]()
6.4 Определение числа зубьев
Определение суммарного числа зубьев
- для прямозубых колес (третья ступень):
zΣ= z1+z2=2aw/m
zΣ=2∙348/7=99.4
Выбираем количество зубьев 99.
-для косозубых колес (первая и вторая ступень)
zΣ= z1+z2=2awсоsβ/m
zΣ1= z1+z2=2∙155соs9/1.75=175
zΣ2= z1+z2=2∙237соs14/4.5=102
Определяем число зубьев шестерни и колеса:
![]()
z2= zΣ-z1
Для первой ступени:
![]()
Принимаем 22 зуба
z2= 175-22=153
Для второй ступени:
![]()
Принимаем 27 зубьев.
z2= 102-27=75
Для третьей ступени:
![]()
Принимаем 31 зуб.
z2= 99-31=68
Похожие работы
... по ступеням и определить силовые и скоростные параметры на валах привода 1.2 Расчетная схема Рисунок 1.1 - Схема для расчета привода пластинчатого конвейера 1.3 Данные для расчета Таблица 1.1 – Данные для расчета привода пластинчатого конвейера Рвых. ,кВт 6 Uобщ. 35 Цилиндрическая передача I прямозубая Цилиндрическая передача II прямозубая Рама Сварная Смазка ...
... a2= m(z1+z2)/2= 0,3(24+49)/2= 10,95 a3= m(z1+z2)/2= 0,3(24+54)/2= 11,7 a4= m(z1+z2)/2= 0,3(24+55)/2= 11,85 a5= m(z1+z2)/2= 0,3(24+68)/2= 13,8 Определим ширину венца: b= (3…15)m= 10·0,3= 3 Определим высоту зуба: h= 2,5m= 2,5·0,3= 0,75 5. Разработка конструкций редуктора Разработка конструкции состоит в расчете и выборе его элементов: зубчатые колеса, валы, подшипники и корпуса. ...
... при проектировании машины, т.е. соответствия этого выбора действующей нормативной документации (НД). 3. Построение компоновки цилиндрического двухступенчатого редуктора Задачей курсовой работы является построение и параметризация компоновочного чертежа многоступенчатого редуктора, поэтому кинематические расчеты производиться не будут и за основу взята модель ранее спроектированного редуктора. ...
... возвращается в исходное положение без слитка, статический момент направлен по угловой скорости вращения кривошипа Мст определится выражением: По данным формулам расчет выполнен в программе Mathcad 12 (приложение 3). Результаты сводим в таблицу 3. 4.2 Расчёт динамического момента Приведенный к оси кривошипа момент инерции для положений механизма 0<φ< π, т.е для точек ...
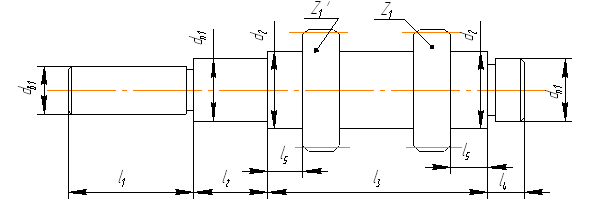
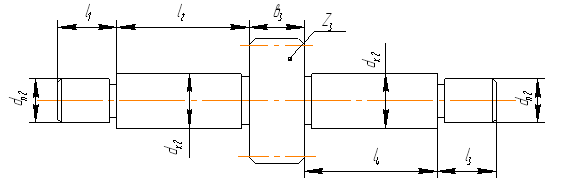
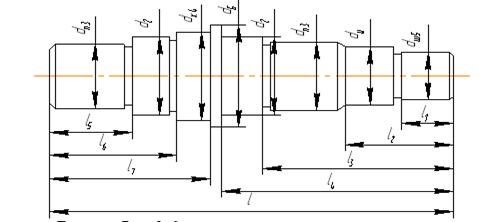
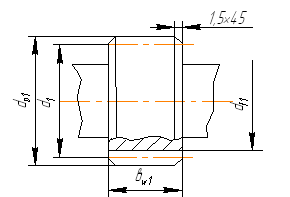


0 комментариев