Навигация
Проверочный расчет тихоходной ступени редуктора
6.6 Проверочный расчет тихоходной ступени редуктора
Проверим зубчатое зацепление на контактные напряжения по формуле:
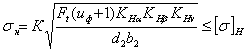 ;
;
где К- вспомогательный. Для прямозубых передач К=436;
Ft=2T2∙103/d2 – окружная сила в зацеплении, Н
KHα– коэффициент, учитывающий распределение нагрузки между зубьями. Для прямозубых колёс KHα=1,
KHv – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи.
Окружная скорость определяется по формуле:
υ=ω2d2/(2∙103)м/с
υ=2.4∙476/(2∙103)=0,57м/с
Исходя из этого KHv=1,23
Вычисляем окружную силу в зацеплении, после чего проверяем контактные напряжения:
Ft =2∙2827∙103/476=11900Н,
![]() , т,е, условие прочности выполнено.
, т,е, условие прочности выполнено.
Проверим напряжения изгиба зубьев шестерни σf1 и колеса σf2, Н/мм2
σf2=YF2Yβ(Ft/b2m)KFαKfβKFv<[σ]f2[3,1]
σf1= σf2 YF1/ YF2<[σ]f1[3,1]
где KFα – коэффициент, учитывающий распределение нагрузки между зубьями. Для прямозубых колес KFα=1;
Kfβ – коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев колес Kfβ=1;
KFv – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи, в данном случае KFv =1,23.
YF1 и YF2 – коэффициенты формы зуба шестерни и колеса, в данном случае YF1=4,27, YF2=3,6,
Yβ – коэффициент учитывающий форму зуба, для прямозубой передачи Yβ=1,
В итоге получаем:
σf2=3,6∙1∙(11900/97∙2.24)∙1∙1∙1,23=242мПа,
σf1=242∙4,27/3,6=287МПа.
Поскольку [σ]f1= [σ]f2=310МПа то условие прочности выполнено.
7. Расчет геометрических параметров валов редуктора
7.1 Ориентировочный расчет геометрических параметров валов редуктора
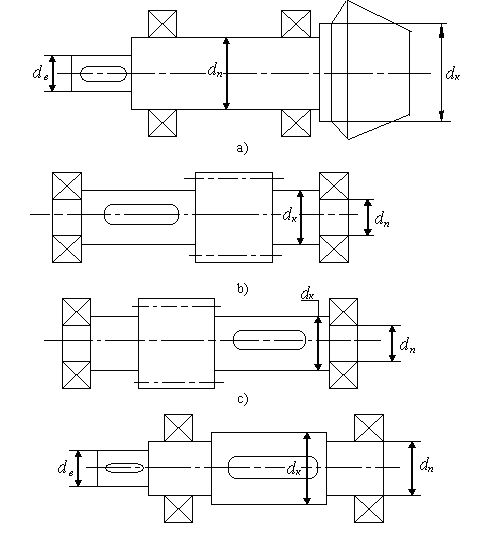
Ориентировочные диаметры валов определяем по формуле:
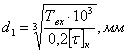 ;
;
где Твх – крутящий момент на быстроходном валу редуктора;
[τ]к – допускаемое напряжение на кручение, принимаемое для среднеуглеродистой стали 25-30Н/мм.
В результате получаем:
- диаметр входного вала под полумуфту
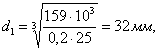 ;
;
Принимаем диаметр вала 32мм.
- диаметр первого промежуточного вала под подшипник:
 ;
;
Принимаем диаметр вала 60мм.
- диаметр второго промежуточного вала под подшипник:

Принимаем диаметр вала 85мм
- диаметр выходного вала под муфту:
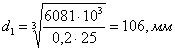
Принимаем диаметр вала 105мм
7.2 Проверочный расчет выходного вала вала
Проверочный расчет вала проводится в виде определения запаса прочности опасного сечения.
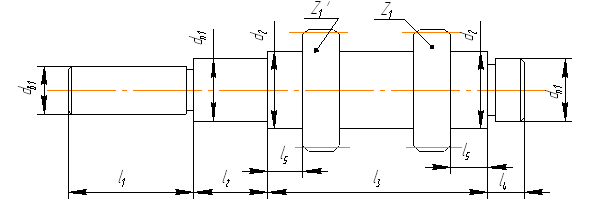
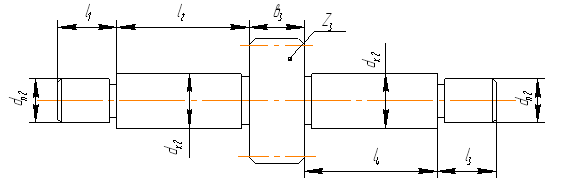
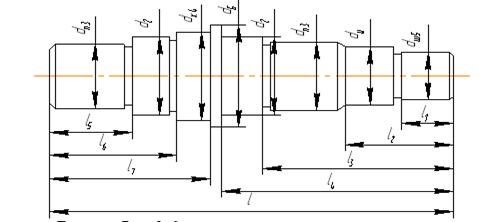
Для определения запаса прочности необходимо определить геометрические параметры вала:
а) длина участка под полумуфту:
l1=(1,0…1,5)105=1.5∙105=165мм,
б) определяем диаметр вала и его длину под уплотнение крышки с отверстием и подшипник:
d2=d1+2t;
где t –высота буртика принимаемая для полученного d1 2,8 мм, т.е. получаем:
d2=105+2∙2,8=110мм, округляем до ближайшего значения диаметра внутреннего кольца подшипника, т.е d2=105мм,
l2=1,5d2=1.1∙105=116мм.
г) определяем диаметр и длину вала под шестерню:
d3=d2+3,2r,
где r – координата фаски подшипника, для вала диаметром 55мм равна 3мм,
d3=105+3,2∙3=115мм.
l3 определяем из соотношения
l3=4a+2b4+b3,
где а=0,003awt+3=0,003∙348+3=4мм
откуда получаем:
l3=3∙4+2∙100+67=279≈300мм,
Действительный коэффициент запаса прочности n должен быть не менее допускаемого т.е.
n≥[n];
С точки зрения обеспечения прочности вала достаточно принять [n]=1,5-1,7. Коэффициент запаса прочности определяется из равенства:
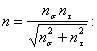
где nσ – коэффициент запаса прочности по нормальным напряжениям;
nτ – коэффициент запаса прочности по касательным напряжениям .
Указанные коэффициенты определяются по формулам:
![]()
![]()
где σ-1 – предел выносливости для материала вала при симметричном цикле изгиба;
τ-1 – предел выносливости при симметричном цикле кручения; можно принимать: τ-1≈0,58 σ-1;
kσ, kτ – эффективные коэффициенты концентрации напряжений при изгибе и при кручении;
εσ, ετ – масштабные факторы для нормальных и касательных напряжений;
σv, σт, τv, τт – амплитуда и среднее напряжение цикла соответственно нормальных и касательных напряжений;
ψσ, ψτ – коэффициенты, отражающие соотношения пределов выносливости при симметричном и пульсирующем циклах соответственно изгиба и кручения.
Можно считать, что амплитуда цикла нормальных напряжений равна наибольшему номинальному напряжению изгиба (σи=Ми/W, где Ми – суммарный изгибающий момент) в рассматриваемом сечении
σv= σт
Т.к. вал не испытывает осевой нагрузки, можно считать, что нормальные напряжения, возникающие в поперечном сечении вала, изменяются по симметричному циклу, т.е. σт=0
В данном случае принимают, что напряжения кручения изменяются по пульсирующему циклу; тогда
![]()
где Мк – крутящий момент;
Wk- момент сопротивления кручению.
Определяем величины необходимые для расчета коэффициента запаса прочности по сечению 1-1(рис7.1):
σ-1=0,43∙590=254 Н/мм2
τ-1≈0,58∙254=147 Н/мм2
kσ=1,6, kτ=1,5
εσ= ετ=0,73
ψσ=0,20, ψτ=0,1
Моменты сопротивления рассчитываются по формулам:
![]() м3
м3
![]() м3
м3
В результате получаем:
![]()
![]()
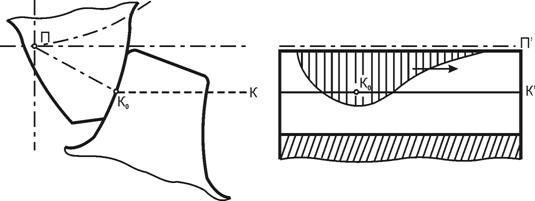
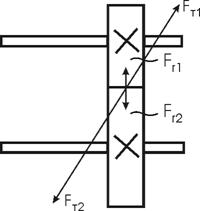
Для определения максимального изгибающего момента строим эпюры изгибающих и крутящих моментов:
Похожие работы
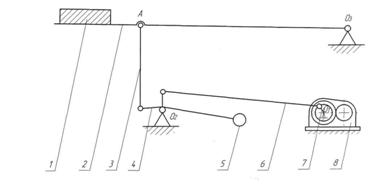
... по ступеням и определить силовые и скоростные параметры на валах привода 1.2 Расчетная схема Рисунок 1.1 - Схема для расчета привода пластинчатого конвейера 1.3 Данные для расчета Таблица 1.1 – Данные для расчета привода пластинчатого конвейера Рвых. ,кВт 6 Uобщ. 35 Цилиндрическая передача I прямозубая Цилиндрическая передача II прямозубая Рама Сварная Смазка ...
... a2= m(z1+z2)/2= 0,3(24+49)/2= 10,95 a3= m(z1+z2)/2= 0,3(24+54)/2= 11,7 a4= m(z1+z2)/2= 0,3(24+55)/2= 11,85 a5= m(z1+z2)/2= 0,3(24+68)/2= 13,8 Определим ширину венца: b= (3…15)m= 10·0,3= 3 Определим высоту зуба: h= 2,5m= 2,5·0,3= 0,75 5. Разработка конструкций редуктора Разработка конструкции состоит в расчете и выборе его элементов: зубчатые колеса, валы, подшипники и корпуса. ...
... при проектировании машины, т.е. соответствия этого выбора действующей нормативной документации (НД). 3. Построение компоновки цилиндрического двухступенчатого редуктора Задачей курсовой работы является построение и параметризация компоновочного чертежа многоступенчатого редуктора, поэтому кинематические расчеты производиться не будут и за основу взята модель ранее спроектированного редуктора. ...
... возвращается в исходное положение без слитка, статический момент направлен по угловой скорости вращения кривошипа Мст определится выражением: По данным формулам расчет выполнен в программе Mathcad 12 (приложение 3). Результаты сводим в таблицу 3. 4.2 Расчёт динамического момента Приведенный к оси кривошипа момент инерции для положений механизма 0<φ< π, т.е для точек ...


0 комментариев