Навигация
Проверка устойчивости замкнутой системы
Проверим устойчивость системы по алгебраическому критерию Гурвица (см. п.1.1).
ХУ ЗС: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Необходимое условие устойчивости выполняется, так как ![]() .
.
Проверим достаточное условие устойчивости. Для системы четвертого порядка достаточно проверить выполнение условия:
![]() ,
,
![]() ,
,
![]() .
.
Условие выполняется, следовательно, система устойчива.
Проверим устойчивость системы по критерию Найквиста [1, §6.5, §6.6].
1. С использованием амплитудно-фазовой частотной характеристики (АФЧХ):
Запишем ПФ РС:
![]() .
.
Для того чтобы судить об устойчивости замкнутой системы, необходимо проверить устойчивость разомкнутой системы. Для этого запишем характеристическое уравнение разомкнутой системы (ХУ РЗ) и найдем корни уравнения:
![]() ,
,
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Так как один из корней равен нулю (![]() ), а все остальные корни с отрицательными вещественными частями (левые), то можно сделать вывод, что разомкнутая система находится на апериодической границе устойчивости.
), а все остальные корни с отрицательными вещественными частями (левые), то можно сделать вывод, что разомкнутая система находится на апериодической границе устойчивости.
Далее необходимо построить АФЧХ разомкнутой системы (годограф Найквиста). Запишем выражение для построения АФЧХ и выделим действительную и мнимую части:
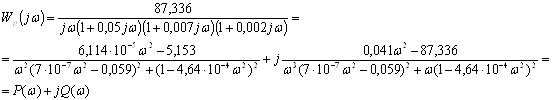
Задаваясь различными значениями ω в пределах от нуля до бесконечности, построим годограф Найквиста (рис. 1.8) по характерным точкам (табл. 1.4):
Таблица 1.4
| ω |
|
|
| 0 | -5,146 | -∞ |
| 46,7 | -0,7 | 0 |
| 290,3 | 0 | 0,008 |
|
| 0 | 0 |
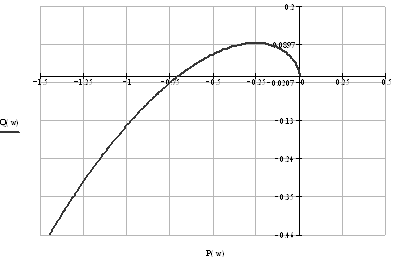
Рис. 1.8. Годограф Найквиста
Так как годограф Найквиста, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывает особую точку (−1;j0), то замкнутая система устойчива.
2. С использованием ЛЧХ:
Запишем выражения и построим ЛАЧХ и ЛФЧХ (рис. 1.9):

![]() .
.

Рис. 1.9. ЛЧХ системы
Замкнутая система устойчива, если выполняется неравенство:
![]() ,
,
где ![]() – частота среза, при которой
– частота среза, при которой ![]() ;
;
![]() – критическая частота, при которой
– критическая частота, при которой ![]() .
.
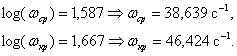
Так как неравенство ![]() выполняется, следовательно, замкнутая система устойчива.
выполняется, следовательно, замкнутая система устойчива.
Проверим устойчивость системы по критерию Михайлова [1, §6.3].
Запишем ХУ ЗС:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Подставим в этот полином чисто мнимое значение ![]() . При этом получим функцию Михайлова, как характеристический полином, состоящий из вещественной и мнимой части:
. При этом получим функцию Михайлова, как характеристический полином, состоящий из вещественной и мнимой части:
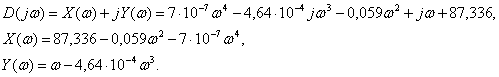
Задаваясь различными значениями ω в пределах от нуля до бесконечности, построим годограф Михайлова (рис. 1.10) по характерным точкам (табл. 1.5):
Таблица 1.5
|
|
|
|
| 0 | 87,336 | 0 |
| 38,82 | 0 | 11,7 |
| 46,424 | -36,683 | 0 |
| 287,71 | 0 | -10763,5 |
| ∞ | ∞ | ∞ |
Так как годограф системы, имеющей четвертый порядок, при изменении ω от 0 до ∞, начинается на вещественной положительной полуоси и при увеличении ω в положительном направлении последовательно проходит четыре квадранта, и при этом не обращается в 0, то можно сделать вывод, что замкнутая система устойчива.
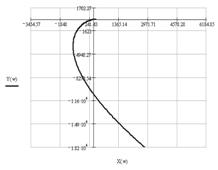
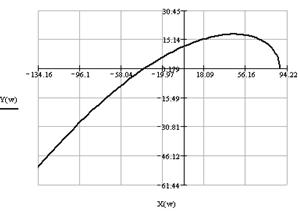 Рис. 1.10. Годограф Михайлова (справа увеличен вблизи начала координат)
Рис. 1.10. Годограф Михайлова (справа увеличен вблизи начала координат)
1.2.3 Определение показателей качества
1. Частота среза разомкнутой системы.
Частота среза разомкнутой системы была определена в анализе системы по критерию Найквиста с использованием ЛЧХ (см. п.1.2.2):
![]() .
.
Похожие работы
... принципиальной схемы приведена в Приложении Б Рисунок 3.7 - Принципиальная электрическая схема корректирующего устройства 4. Экономический расчет Затраты на проектирование цифрового регулятора для электропривода с фазовой синхронизацией определяются по формуле: , (1.1) где Сосн, зп - основная заработная плата персонала, руб.; Сдоп, зп - дополнительная заработная плата ...
... Национальный Технический Университет Кафедра Технической кибернетики ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовому проекту по курсу «Проектирование систем автоматического управления» «Проектирование системы автоматического регулирования угла поворота вала электродвигателя» Выполнила: ст. гр. А – 61з Брусинов С. Э. Проверил: Дубовик С.А. Оценка ________________ Дата «____» ...
... и конструкций значительно влияет на: сокращение стоимости отделки зданий сооружений; трудоемкость; расход основных материалов; число ремонтов и их стоимость. Глава 3. Улучшение деятельности в процессах 3.1 Исследование и анализ процессов управления системы менеджмента качества Стандарты ИСО 9001: 2000 предлагают новый подход к построению СМКп, которая состоит из (рис.3.1): -политики в ...
... методику проектирования систем регулирования и позволяет создавать высокоэффективные автоматические системы для самых различных отраслей народного хозяйства. Полученные таким образом системы автоматического регулирования обеспечивают высокое качество выпускаемой продукции, снижают ее себестоимость и увеличивают производительность труда. 1. Общая часть. 1.1. Основные понятия Преобразование ...
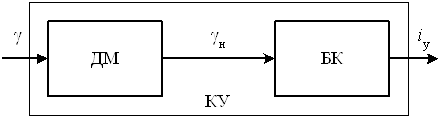


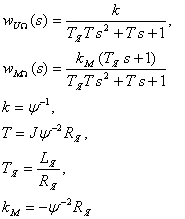






0 комментариев