Навигация
1 Випадкова величина. Функція розподілу випадкової величини
Зіставимо кожну елементарну подію конкретного випробування з деяким числом. Наприклад, розглянемо випробування, що полягає в підкиданні монети. Маємо простір елементарних подій – множину з двох можливих рівно ймовірних наслідків випробування: w1 – випадання "решки" та w2 – випадання герба. Введемо до розгляду функцію x= f(w), що визначається за формулами: f(w1)=0, f(w2)=1. Це – числова функція (випадкова величина), яка залежить від випадку. Позначимо її через ![]() :
:
![]()
Для значень, яких у результаті випробувань може рівно ймовірно набувати функція ![]() , застосуємо символи
, застосуємо символи ![]() та
та ![]() . Відповідно з нашою угодою, вони дорівнюють
. Відповідно з нашою угодою, вони дорівнюють
![]() і
і ![]()
У загальному випадку задовільної випадкової величини позначатимемо її однією з грецьких літер x,h,..., а значення, яких вона набуває літерами латинської абетки: х, y,..... Відповідність між цими значеннями та ймовірностями, з якими їх набуває така функція ![]() , зручно задати у вигляді табл. 1, що називається законом розподілу дискретної випадкової величини:
, зручно задати у вигляді табл. 1, що називається законом розподілу дискретної випадкової величини:
Таблиця 1
|
|
|
|
| ... |
|
|
|
|
|
| ... |
|
У випадку зазначеної конкретної випадкової величини, пов’язаної з випадінням сторін підкинутої монети, табл. 1 конкретизується у вигляді табл. 2:
Таблиця 2
|
| 0 | 1 |
|
| 1/2 | 1/2 |
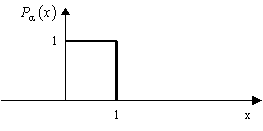
Цю закономірність можна також наочно представити на площині xOy, розмістивши на горизонтальній осі значення ![]() і
і ![]() , а на вертикальній осі, що доцільно було перемістити з її традиційного положення – відповідні їм ймовірності (рис. 1). При цьому графік функції
, а на вертикальній осі, що доцільно було перемістити з її традиційного положення – відповідні їм ймовірності (рис. 1). При цьому графік функції ![]() складається тільки з двох точок (
складається тільки з двох точок (![]() ,
,![]() ) і (
) і (![]() ,
,![]() ). В інших точках горизонтальної осі функція
). В інших точках горизонтальної осі функція ![]() взагалі принципово не визначена.
взагалі принципово не визначена.
Ще більш наочно закон розподілу дискретної випадкової величини зображається специфічною функцією
![]()
що називається функцією розподілу випадкової величини ![]() .
.
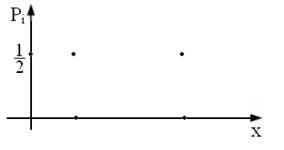
Рисунок 1
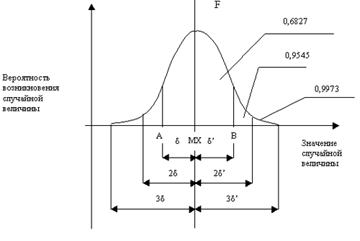
У відповідності з її визначенням, вона дає в точці x ймовірність того, що випадкова величина розташована на осі Ox зліва від цієї точки x. Зокрема, для випадкової величини, заданої законом розподілу в табл. 2, ця функція має складний вигляд із різними представленнями на різних інтервалах
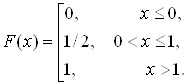
На рис. 2 наведено її графік з двома неусувними розривами 1-го роду.
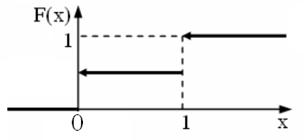
Рисунок 2
Розглянемо ще один приклад введення випадкової величини. Нехай є мішень – круг радіуса а, влучення до якого гарантовано. Як випадкову величину, що позначимо як ![]() , візьмемо відстань від центра мішені до точки влучення. Ймовірність того, що ця випадкова величина набуває різних значень r від нуля до а, обчислюється за формулою геометричної ймовірност:
, візьмемо відстань від центра мішені до точки влучення. Ймовірність того, що ця випадкова величина набуває різних значень r від нуля до а, обчислюється за формулою геометричної ймовірност:
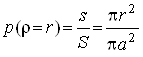
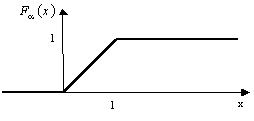
При цьому функція розподілу
![]()
графік якої зображено на рис. 3, має вигляд
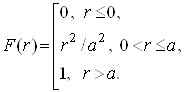
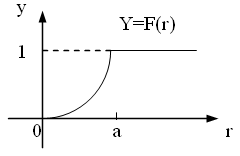
Рисунок 3
Модифікуємо попередній приклад: нехай всередині круга радіуса а, влучення до якого гарантовано, проведено два концентричні кола (рис. 4) з радіусами a/3 і 2a/ В залежності від відстані точки влучення від центра мішені стрілець одержує 10, 5 чи 1 бал, відповідно.
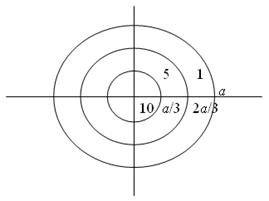
Рисунок 4
За випадкову величину, що позначимо як ![]() , візьмемо тепер кількість очок, набраних при пострілі по мішені. Її можливі значення: 10, 5, 1. Обчислимо ймовірності випадків прийняття цих значень величиною
, візьмемо тепер кількість очок, набраних при пострілі по мішені. Її можливі значення: 10, 5, 1. Обчислимо ймовірності випадків прийняття цих значень величиною ![]()
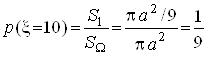 ,
,
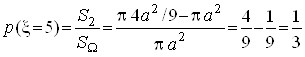 ,
,
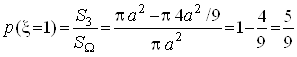
При цьому закон розподілу випадкової величини ![]() має вигляд табл. 3:
має вигляд табл. 3:
Таблиця 3
|
| 1 | 5 | 10 |
|
| 5/9 | 1/3 | 1/9 |
За цим законом розподілу випадкової величини ![]() знаходимо функцію її розподілу та будуємо її графік (рис. 5).
знаходимо функцію її розподілу та будуємо її графік (рис. 5).
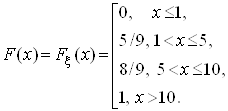
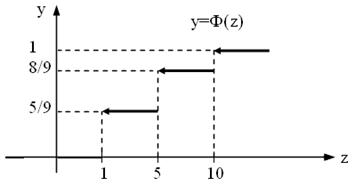
Рисунок 5
Властивості функції розподілу:
1. F(x) – неубутна функція. Дійсно, якщо x1<x2 (рис. 6).
![]()
Рисунок 6
F(x2)=P(x<x2)=P(x<x1)+P(x1<x<x2)>P(x<x1)=F(x1); F(x1)<F(x2);
Похожие работы
... рівність нормування . Ймовірність попадання випадкової точки у довільну область (рис.1.3) обчислюється за формулою ,(1.7) яка одразу слідує з означення подвійного інтеграла Приклад 1.5. Система випадкових величин задана густиною сумісного розподілу . Знайти ймовірність попадання випадкової точки у прямокутник з вершинами , ,,. Розв’язування. За формулою (1.7) . . ...
... ідністю варіювати значення ціни як безперервної випадкової величини. З курсу математичної статистики відомо, що математичне очікування нормально розподіленої випадкової величини можна представити у вигляді: (1.1) Практичне застосування даної формули при оцінці ризику в ціноутворенні вимагає її спрощення. Не утрудняючи читача відомими [1,3], але громіздкими перетвореннями одержуємо: ...
... вибірка із незалежних реалізацій БВВ , яка в подальшому використовується для побудови ВЕ із необхідними ймовірнісними характеристиками. При моделюванні на ЕОМ складних ВЕ, зокрема, випадкової величини (ВВ) або випадкового процесу (ВП) з заданими ймовірнісними характеристиками розглядається складний випадковий експеримент, що полягає в проведенні раз описаного вище найпростішого експерименту. ...
... , . . Для опису зв'язків, що існують між проекціями випадкового вектора (x,h), крім коваріації можна використовувати числові характеристики умовних законів розподілу , . Умовним середнім значенням і умовною дисперсією випадкової величини x за умови h =y називаються величини: , . Аналогічно визначаються характеристики і . Для опису випадкового вектора також вводять початкові і ...
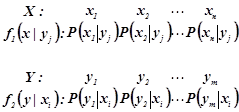
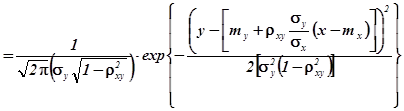






0 комментариев