Навигация
F(+¥)=1; F(-¥)=0; F(+¥)=P(x<¥)=1;
2. F(+¥)=1; F(-¥)=0; F(+¥)=P(x<¥)=1;
P(-¥<x<¥)=1; F(-¥)=0;
P(a£x<b)=P(x<b) - P(x<a)=Fx(b) - Fx(a).
Якщо функція розподілу в деякій точці x=а має неусувний розрив 1-го роду – стрибок на величину р, (рис. 7) то Р(x=а)=р.
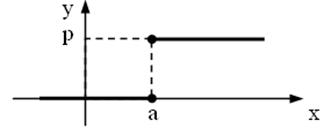
Рисунок 7
Дійсно, розглянемо [а, b), b® a+0.
P(x=а)=![]() .
.
Найбільш важливими типами випадкових величин є дискретні і неперервні випадкові величини, які будуть розглянуті більш докладно.
2 Дискретна випадкова величина Випадкова величина називається дискретною, якщо її можливі значення можна перенумерувати.
Нехай х1,х2,…,хn – можливі значення дискретної випадкової величини в порядку зростання.
Випадкові події [x=x1], [x=x2], …[x=xn] утворять повну систему елементарних подій. При цьому
![]() ,
, 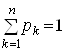
Закон розподілу дискретної випадкової величини можна задати таблицею (табл. 1) чи геометрично – точками на площині (xi, pi); або ламаною, що з'єднує ці точки та називається багатокутником розподілу (рис. 8):
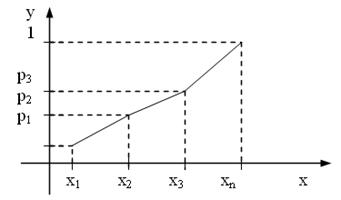
Рисунок 8
Цьому закону розподілу є відповідною функція розподілу ![]()
Fx(x)=P(x<x)=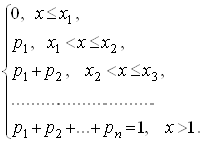
або
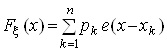
де
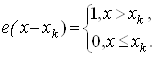
Її графік наведено на рис. 9
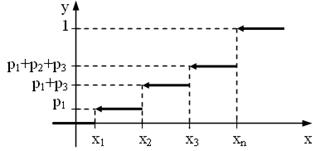
Рисунок 9
Як видно з рис. 9, функція розподілу дискретної випадкової величини є кусково неперервною. У точці хi вона зростає на величину ![]() . При цьому
. При цьому
![]() .
.
3 Найважливіші закони розподілу дискретних випадкових величин
Біноміальний розподіл. Розглядається серія з n випробувань, у кожному з яких подія А відбувається або не відбувається. Ймовірність появи події А в кожному випробуванні постійна і не залежить від результатів інших випробувань. Це схема Бернуллі:
Р(А)=р; ![]() .
.
Як випадкову величину, яку позначимо ![]() , розглянемо кількість появ події А у n випробуваннях. Не важко перевірити, що ймовірність появи події
, розглянемо кількість появ події А у n випробуваннях. Не важко перевірити, що ймовірність появи події ![]() визначається формулою Бернуллі у вигляді
визначається формулою Бернуллі у вигляді
![]() ; (1)
; (1)
де ![]() – кількість сполучень з
– кількість сполучень з ![]() елементів по
елементів по ![]() (1).
(1).
Відповідний цїй формулі закон розподілу випадкової величини називається біноміальним, тому що його коефіцієнти збігаються з коефіцієнтами членів розкладання бінома Ньютона (p+q)n (табл. 4).
Таблиця 4
| xn | 0 | 1 | … | k | … | n |
| pn | qn | npqn-1 | … |
| … | pn |
Нехай кількість випробувань ![]() необмежено зростає, але так, щоб її добуток на ймовірність появи події A в кожному випробуванні, тобто
необмежено зростає, але так, щоб її добуток на ймовірність появи події A в кожному випробуванні, тобто ![]() , залишався скінченою величиною порядку одиниці. Це передбачає дуже мале значення ймовірності
, залишався скінченою величиною порядку одиниці. Це передбачає дуже мале значення ймовірності ![]() , отже розглядаються дуже рідкі події та дуже довгі серії випробувань. При формалізації відзначених умов у формулі Бернуллі (1) можна перейти до границі
, отже розглядаються дуже рідкі події та дуже довгі серії випробувань. При формалізації відзначених умов у формулі Бернуллі (1) можна перейти до границі ![]()

або остаточно отримати формулу Пуассона для ймовірності появи ![]() разів дуже рідкої події A у практично нескінченних випробуваннях
разів дуже рідкої події A у практично нескінченних випробуваннях
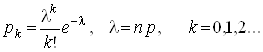
Розподіл випадкової величина ![]() за цією формулою називається законом Пуассона (законом рідкісних подій). Число l називається параметром розподілу. Цей закон можна подати у вигляді:
за цією формулою називається законом Пуассона (законом рідкісних подій). Число l називається параметром розподілу. Цей закон можна подати у вигляді:
Таблиця 5
| x | 0 | 1 | … | k | … |
| p | e-l | le-l | … |
| … |
Розглянемо типову задачу, що приводить до розподілу Пуассона. Нехай подія А означає відмову складного пристрою протягом малого проміжку часу. Причиною відмови є вихід з ладу будь-якої деталі. Режим роботи пристрою не змінюється з часом, відмова окремих деталей відбувається незалежно одна від одної, причому за одиницю часу "в середньому" відбувається l відмовлень.
При цих допущеннях з великим ступенем точності виконуються такі умови:
1. Ймовірність появи відмови на проміжку часу (0, Т) така сама, як і на задовільному проміжку довжиною T (t,t+T).
2. Появи відмовлень на проміжках часу, що не перекриваються, незалежні.
Ймовірність появи відмовлення за нескінченно малий проміжок часу визначається за формулою:
р(А)=l Dt+o(Dt), Dt®0.
4. Імовірність появи більше однієї відмови є о(Dt), Dt®0.
Розіб'ємо інтервал (t,t+T) на n рівних частин ![]() .
.
Розглядатимемо реєстрацію відмови як окреме випробування
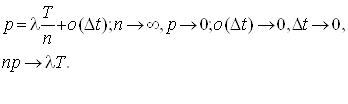
При цьому приходимо до розподілу Пуассона для кількості відмовлень за час Т
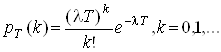
Геометричний закон розподілу. Проводиться серія випробувань до першої появи події А. Ймовірність появи події А в кожному випробуванні дорівнює р і не залежить від інших випробувань.
Як випадкову величину ![]() розглядатимемо кількість проведених випробувань, необхідних для першої появи події А. Очевидно, що закон розподілу цієї випадкової величини можна подати таблицею:
розглядатимемо кількість проведених випробувань, необхідних для першої появи події А. Очевидно, що закон розподілу цієї випадкової величини можна подати таблицею:
Таблиця 6
| x | 1 | 2 | 3 | … | k |
| P | P | qp | q2p | … | qk-1p |
Похожие работы
... рівність нормування . Ймовірність попадання випадкової точки у довільну область (рис.1.3) обчислюється за формулою ,(1.7) яка одразу слідує з означення подвійного інтеграла Приклад 1.5. Система випадкових величин задана густиною сумісного розподілу . Знайти ймовірність попадання випадкової точки у прямокутник з вершинами , ,,. Розв’язування. За формулою (1.7) . . ...
... ідністю варіювати значення ціни як безперервної випадкової величини. З курсу математичної статистики відомо, що математичне очікування нормально розподіленої випадкової величини можна представити у вигляді: (1.1) Практичне застосування даної формули при оцінці ризику в ціноутворенні вимагає її спрощення. Не утрудняючи читача відомими [1,3], але громіздкими перетвореннями одержуємо: ...
... вибірка із незалежних реалізацій БВВ , яка в подальшому використовується для побудови ВЕ із необхідними ймовірнісними характеристиками. При моделюванні на ЕОМ складних ВЕ, зокрема, випадкової величини (ВВ) або випадкового процесу (ВП) з заданими ймовірнісними характеристиками розглядається складний випадковий експеримент, що полягає в проведенні раз описаного вище найпростішого експерименту. ...
... , . . Для опису зв'язків, що існують між проекціями випадкового вектора (x,h), крім коваріації можна використовувати числові характеристики умовних законів розподілу , . Умовним середнім значенням і умовною дисперсією випадкової величини x за умови h =y називаються величини: , . Аналогічно визначаються характеристики і . Для опису випадкового вектора також вводять початкові і ...
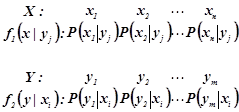
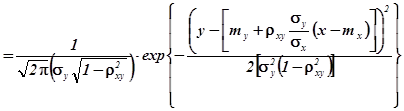






0 комментариев