Навигация
2.6 Определение медианы
Если количество вариант число четное, то медиана вычисляется по формуле:
МВ=(xk+xk+1)/2 (2.5.)
где xk – пятидесятый член вариационного ряда;
xk+1 – пятьдесят первый член вариационного ряда;
n – Количество вариант и n=2*k
МВ=(xk+xk+1)/2=(-689–689)/2= -689
2.7 Расчет коэффициента вариации
Расчет коэффициента вариации проведем по формуле:
![]() (2.6)
(2.6)
![]()
Вывод:
Размах варьирования является простейшей характеристикой рассеяния вариационного ряда.
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводные характеристики – генеральную дисперсию и средним квадратическим отклонением.
Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние, у которого коэффициент больше (эта величина безразмерная поэтому он пригоден для сравнения вариационных рядов, варианты которых имеют различную размерность.
В целом числовые характеристики служат для сравнения рассеяния вариационных рядов в сравнении с аналогичными числовыми характеристиками других вариационных рядов.
3. Построение полигона и гистограммы относительных частот
Для построения гистограммы и полигона относительных частот поделим вариационный ряд (табл. 1) на частичные интервалы. Результаты занесем в таблицу 3.
Таблица 3
| Номер интервала I | Частичный интервал xi–xx+1 | Сумма относительных частот wi | Плотность частот
| |
| xi | xx+1 | |||
| 1 | -805 | -780,6 | 0,01 | 0,00041 |
| 2 | -780,6 | -756,2 | 0,02 | 0,00082 |
| 3 | -756,2 | -731,8 | 0,03 | 0,00123 |
| 4 | -731,8 | -707,4 | 0,12 | 0,00492 |
| 5 | -707,4 | -683 | 0,4 | 0,01639 |
| 6 | -683 | -658,6 | 0,24 | 0,00984 |
| 7 | -658,6 | -634,2 | 0,08 | 0,00328 |
| 8 | -634,2 | -609,8 | 0,05 | 0,00205 |
| 9 | -609,8 | -585,4 | 0,03 | 0,00123 |
| 10 | -585,4 | -561 | 0,02 | 0,00082 |
По таб. 3 строим гистограмму относительных частот (рис. 1).
Полигон получаем соединением вершин столбцов гистограммы. (рис. 1) Полигон получаем соединением вершин столбцов гистограммы.
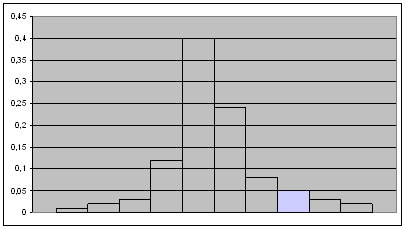
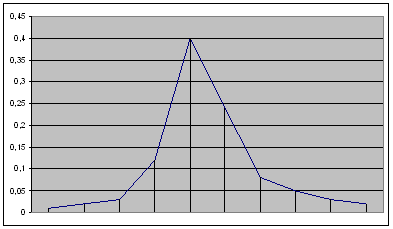
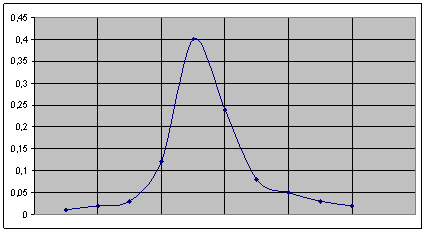
Рис 1.
Вывод: Полигон и гистограмму – графики статистического распределения строят для наглядности относительных частот в выборке.
Похожие работы
... называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением. 2. Методы вторичной статистической обработки результатов эксперимента С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, ...
... В.Ю. Геометрическое представление данных психологических исследований. – М.: Наука. – 1990. 8. Лакин Г.Ф. Биометрия. – М.: Высшая школа. – 1973. – 343 с. 9. Лбов Г.С. Методы обработки разнотипных данных. – М.: Наука. – 1981. 10. Математические методы в исследованиях индивидуальной и групповой деятельности п/ред. Крылова В.Ю. – М.: Наука. – 1990. 11. Мацкевич И.П., ...
... отпуска может быть на 10–20оС ниже, а его продолжительность на 20–25% меньше, чем первого отпуска. Охлаждение после отпуска проводится на воздухе. 1.1.5 Влияние термической обработки на свойства штамповых сталей Служебные свойства штампового инструмента и его стойкость в значительной степени определяются соответствующим назначением марки стали, ее термообработкой и условиями эксплуатации ...
... силы взаимодействия между рыбой и рабочими органами машин, поскольку изменяется площадь контакта, обусловливающая силы трения. До настоящего времени структурно-механические характеристики в основном оцениваются органолептическим методом. Рыбу сдавливают пальцами и оценивают ее консистенцию. Не достатком такого метода оценки структурно-механических характеристик мышечной ткани является его ...
0 комментариев