Навигация
Статистическая проверка гипотезы о нормальном распределении с помощью критерия Пирсона или Колмагорова
11726
знаков
8
таблиц
4
изображения
5. Статистическая проверка гипотезы о нормальном распределении с помощью критерия Пирсона или Колмагорова
Проверку проводим с помощью критерия Пирсона.
В этом задании, с помощью критерии Пирсона проверим гипотезу о нормальном распределении генеральной совокупности, с этой целью будем сравнивать эмпирические и теоретические частоты.
– Среднее арифметическое значение
– Количество вариантов
– Шаг интервалов
– Оценка среднеквадратического отклонения.
Вычислим данные по таблице:
| ||||||||||||
| I | ni | Xi | X (i+1) | Zi | Z (I+1) |
|
|
|
|
| ||
| 1 | 1 | -805 | -780,6 | -2,7340 | -0,5 | -0,469 | 3,1 | 1,4226 | 0,3226 | |||
| 2 | 1 | -780,6 | -756,2 | -2,7340 | -2,1140 | -0,469 | -0,408 | 6,1 | 4,2639 | 0,1639 | ||
| 3 | 4 | -756,2 | -731,8 | -2,1140 | -1,4941 | -0,408 | -0,285 | 12,3 | 5,6008 | 1,3008 | ||
| 4 | 7 | -731,8 | -707,4 | -1,4941 | -0,8741 | -0,285 | -0,099 | 18,6 | 7,2344 | 2,6344 | ||
| 5 | 26 | -707,4 | -683 | -0,8741 | -0,2542 | -0,099 | 0,1141 | 21,31 | 1,0322 | 31,7222 | ||
| 6 | 33 | -683 | -658,6 | -0,2542 | 0,3658 | 0,1141 | 0,2939 | 17,98 | 12,5473 | 60,5673 | ||
| 7 | 14 | -658,6 | -634,2 | 0,3658 | 0,9857 | 0,2939 | 0,4131 | 11,92 | 0,3630 | 16,4430 | ||
| 8 | 8 | -634,2 | -609,8 | 0,9857 | 1,6057 | 0,4131 | 0,4713 | 5,82 | 0,8166 | 10,9966 | ||
| 9 | 3 | -609,8 | -585,4 | 1,6057 | 2,2256 | 0,4713 | 0,4927 | 2,14 | 0,3456 | 4,2056 | ||
| 10 | 3 | -585,4 | -561 | 2,2256 | 0,4927 | 0,5 | 0,73 | 7,0588 | 12,3288 | |||
| СУММА | 100 | 100 | 40,6851 | 140,6851 | ||||||||
X2набл=40,685
Контроль: 
140,685–100=40,685
Исходя из требований, чтобы вероятность попадания критерия в критическую область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 
.
Таким образом, правосторонняя критическая область определяется неравенством 
, а область принятия нулевой гипотезы – неравенством
.
Уровень значимости = 0,05;
По таблице критических точек распределения χ² (приложение 3), по уровню значимости α = 0,05 и числу степеней свободы K=10–3=7 находим критическую точку правосторонней критической области χ²кр (0,05; 7) = 14,1.
Вывод: Так как X2набл> X2кр, то нулевую гипотезу отвергают, значит гипотезу о нормальном распределении отвергают.
Похожие работы
... называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением. 2. Методы вторичной статистической обработки результатов эксперимента С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, ...
... В.Ю. Геометрическое представление данных психологических исследований. – М.: Наука. – 1990. 8. Лакин Г.Ф. Биометрия. – М.: Высшая школа. – 1973. – 343 с. 9. Лбов Г.С. Методы обработки разнотипных данных. – М.: Наука. – 1981. 10. Математические методы в исследованиях индивидуальной и групповой деятельности п/ред. Крылова В.Ю. – М.: Наука. – 1990. 11. Мацкевич И.П., ...
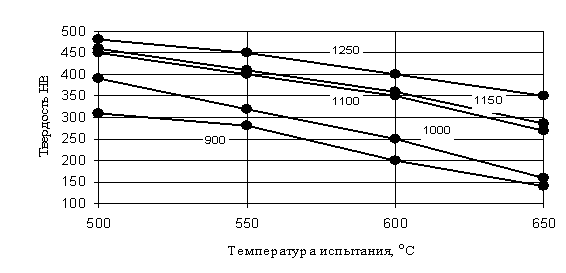
... отпуска может быть на 10–20оС ниже, а его продолжительность на 20–25% меньше, чем первого отпуска. Охлаждение после отпуска проводится на воздухе. 1.1.5 Влияние термической обработки на свойства штамповых сталей Служебные свойства штампового инструмента и его стойкость в значительной степени определяются соответствующим назначением марки стали, ее термообработкой и условиями эксплуатации ...
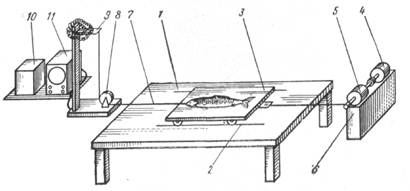
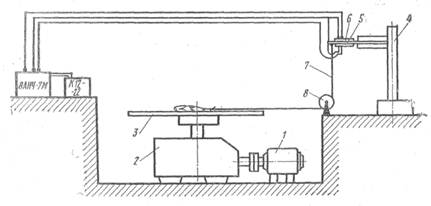
... силы взаимодействия между рыбой и рабочими органами машин, поскольку изменяется площадь контакта, обусловливающая силы трения. До настоящего времени структурно-механические характеристики в основном оцениваются органолептическим методом. Рыбу сдавливают пальцами и оценивают ее консистенцию. Не достатком такого метода оценки структурно-механических характеристик мышечной ткани является его ...
0 комментариев