Навигация
Расчет асимметрии и эксцесса
6. Расчет асимметрии и эксцесса
Асимметрия – отношение центрального момента 3-го порядка к кубу среднего квадратического отклонения.
![]() , где
, где ![]()
Эксцесс – характеристика «крутости» рассматриваемой случайной величины.
![]() , где
, где ![]()
Значение ХВ, s вычисляем по формулам:
![]() ,
,
где С – Ложный нуль (варианта, которая имеет наибольшую частоту).
![]() ,
,
где h – шаг (разность между двумя соседними вариантами);
![]() (условный момент второго порядка);
(условный момент второго порядка);
![]() (условный момент первого порядка);
(условный момент первого порядка);
![]() (условная варианта).
(условная варианта).
Расчеты занесем в таблицу 7:
| Xi | Ni | Ui | XB | M1 | M2 | s | m3 | m4 | AS | EK |
| -805 | 1 | -2,73 | -684,67 | 0,30 | 1,06 | 23,97 | 3433,28 | 4193007,72 | 0,25 | 12,71 |
| -780,6 | 1 | -2,11 | ||||||||
| -756,2 | 4 | -1,49 | ||||||||
| -731,8 | 7 | -0,87 | ||||||||
| -707,4 | 26 | -0,25 | ||||||||
| -683 | 33 | 0,37 | ||||||||
| -658,6 | 14 | 0,99 | ||||||||
| -634,2 | 8 | 1,61 | ||||||||
| -609,8 | 3 | 2,23 | ||||||||
| -585,4 | 3 | 2,85 |
Вывод:
Т.к. асимметрия положительна то ‘длинная часть’ кривой распределения расположена справа от математического ожидания или мода.
Т.к. Эксцесс больше нуля, то кривая распределения имеет более высокую и ‘острую’ вершину, чем нормальная кривая.
7. Построение доверительного интервала для математического ожидания и среднего квадратического отклонения
Доверительный интервал для математического ожидания (с вероятностью g) находят как:
![]() (7.1)
(7.1)
где n – объем выборки;
tg – случайная величина имеющее распределение Стьюдента находим по приложению 1.
s – исправленное среднее квадратическое отклонение;
![]() – выборочное среднее;
– выборочное среднее;
Найдем интервал:
по приложению 1 находим tg= 1.984 при g = 0.95 и n = 100;
![]() =-684,67; s = 38,19;
=-684,67; s = 38,19;
Получаем
![]()
-692,25<a<-677.09
Доверительный интервал для среднего квадратического отклонения
(с надежностью g) находят как:
![]() при q<1 (7.2)
при q<1 (7.2)
![]() при q>1 (7.3)
при q>1 (7.3)
где q находят по приложению 2, по заданным n и g;
Исходя из приложения 2, n = 100 и g = 0.95 находим q=0.143;
Поэтому интервал находим по формуле (7.2):
|
32.73 < ![]() < 43.65
< 43.65
Вывод:
Итак, с надежностью 0,95 неизвестное математическое ожидание ‘а’ находится в доверительном интервале -692,25<a<-677.09, а неизвестное среднее квадратическое отклонение ‘’ находиться в доверительном интервале 32.73 < ![]() < 43.65.
< 43.65.
Вывод
Для представления генеральной совокупности я исследовала выборку, которая имеет объём 100 элементов.
Я нашла:
размах варьирования R=244;
среднеарифметическое значение статистического ряда ![]() =-684,67;
=-684,67;
несмещенную оценку генеральной дисперсии s2=1458,99;
среднее квадратическое отклонение s=38,19;
медиану МВ=-689 и коэффициент вариации V= ![]() 5,58%.
5,58%.
С надежностью 0.95 оценил математическое ожидание в интервале
-692,25< а < -677,09
и среднее квадратическое отклонение в интервале
32,73 < ![]() < 43,65
< 43,65
Выборка имеет варианты x = -731, x = -703, x = -701, x = -700, x = -697, x = -689, x = -686, x = -681, x = -667, которые встречаются 3 раза.
На рис. 1 построила гистограмму и полигон относительных частот. По рис. 1 можно выдвинуть гипотезу о нормальном распределении генеральной совокупности.
После проверки гипотезы о нормальном распределении с помощью критерия Пирсона при a=0.05, я отвергла ее. Из этого следует, что расхождения между практическими и теоретическими частотами значимо.
Асимметрия as=0,25. Из этого следует, что правое крыло функции более вытянуто относительно ее моды.
Эксцесс ek=12,71. Из-за того, что у эксцесса положительный знак, эмпирическая функция распределения острее по сравнению с теоретическим распределением.
Список литературы
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 2001.
2. Гмурман В.Е. Теория вероятностей и математическая статистика.
М.: Высшая школа, 2001.
Похожие работы
... называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением. 2. Методы вторичной статистической обработки результатов эксперимента С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, ...
... В.Ю. Геометрическое представление данных психологических исследований. – М.: Наука. – 1990. 8. Лакин Г.Ф. Биометрия. – М.: Высшая школа. – 1973. – 343 с. 9. Лбов Г.С. Методы обработки разнотипных данных. – М.: Наука. – 1981. 10. Математические методы в исследованиях индивидуальной и групповой деятельности п/ред. Крылова В.Ю. – М.: Наука. – 1990. 11. Мацкевич И.П., ...
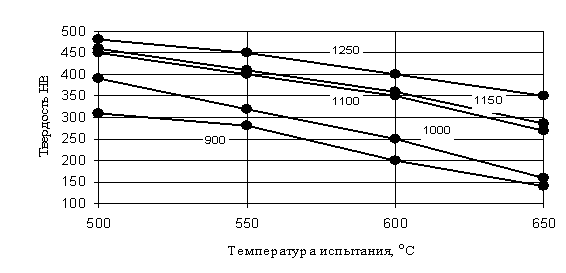
... отпуска может быть на 10–20оС ниже, а его продолжительность на 20–25% меньше, чем первого отпуска. Охлаждение после отпуска проводится на воздухе. 1.1.5 Влияние термической обработки на свойства штамповых сталей Служебные свойства штампового инструмента и его стойкость в значительной степени определяются соответствующим назначением марки стали, ее термообработкой и условиями эксплуатации ...
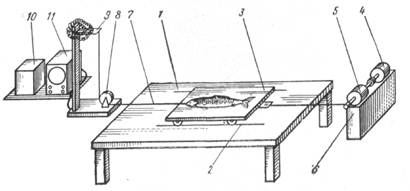
... силы взаимодействия между рыбой и рабочими органами машин, поскольку изменяется площадь контакта, обусловливающая силы трения. До настоящего времени структурно-механические характеристики в основном оцениваются органолептическим методом. Рыбу сдавливают пальцами и оценивают ее консистенцию. Не достатком такого метода оценки структурно-механических характеристик мышечной ткани является его ...
0 комментариев