Навигация
Элементы теории множеств
Федеральное агентство по образованию
ФГОУ ВПО
Чувашский государственный университет им. И.Н. Ульянова
Алатырский филиал
Факультет управления и экономики
Кафедра высшей математики и информационных технологий
Курсовая работа
по дисциплине: Математическая логика
Элементы теории множеств
Выполнил студент
1 курса
группы - АФТ 61-06
Научный руководитель
проф. Мерлин А.В.
Алатырь
Введение
Теория множеств – раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики.
До второй половины XIX века понятие «множества» не рассматривалось в качестве математического (множество книг на полке, множество человеческих добродетелей и т. д. — всё это чисто бытовые обороты речи). Положение изменилось, когда немецкий математик Георг Кантор (рис. 1) разработал свою программу стандартизации математики, в рамках которой любой математический объект должен был оказываться тем или иным «множеством».
Например, натуральное число, по Кантору, следовало рассматривать как множество, состоящее из единственного элемента другого множества, называемого «натуральным рядом» — который, в свою очередь, сам представляет собой множество, удовлетворяющее так называемым аксиомам Пеано. При этом общему понятию «множества», рассматривавшемуся им в качестве центрального для математики, Кантор давал мало что определяющие определения вроде «множество есть многое, мыслимое как единое», и т. д. Это вполне соответствовало умонастроению самого Кантора, подчёркнуто называвшего свою программу не «теорией множеств» (этот термин появился много позднее), а учением о множествах (Mengenlehre).
Программа Кантора вызвала резкие протесты со стороны многих современных ему крупных математиков. Особенно выделялся своим непримиримым к ней отношением Леопольд Кронекер, полагавший, что математическими объектами могут считаться лишь натуральные числа и то, что к ним непосредственно сводится (известна его фраза о том, что «бог создал натуральные числа, а всё прочее — дело рук человеческих»). Тем не менее, некоторые другие математики — в частности, Готлоб Фреге и Давид Гильберт — поддержали Кантора в его намерении перевести всю математику на теоретико-множественный язык.
Однако вскоре выяснилось, что установка Кантора на неограниченный произвол при оперировании с множествами (выраженный им самим в принципе «сущность математики состоит в её свободе») является изначально порочной. А именно, был обнаружен ряд теоретико-множественных антиномий: оказалось, что при использовании теоретико-множественных представлений некоторые утверждения могут быть доказаны вместе со своими отрицаниями (а тогда, согласно правилам классической логики высказываний, может быть «доказано» абсолютно любое утверждение!). Антиномии ознаменовали собой полный провал программы Кантора.
И всё же Кантор считается основателем теории множеств, и сделал большой вклад в современную математику. Ему принадлежит следующая характеристика понятия «множество»: Множество — это объединение определённых, различных объектов, называемых элементами множества, в единое целое.
Глава 1. Множества
1.1 Элементы и множества
Понятия множества и элемента множества относятся к понятиям, не определимым явно, таким, как, например, точка и прямая. Слова «совокупность», «семейство», «система», «набор» и т.п. – синонимы слова «множество». Это связано с тем, что некоторые понятия в математике должны быть исходными, служить теми "кирпичиками", из которых складывается общая теория. Мы определяем только, как соотносятся эти исходные понятия, не говоря о природе рассматриваемых объектов. Человеческое мышление устроено так, что мир представляется состоящим из отдельных «объектов». Философам давно ясно, что мир — единое неразрывное целое, и выделение в нем объектов — это не более чем произвольный акт нашего мышления, позволяющий сформировать доступную для рационального анализа картину мира. Но как бы там ни было, выделение объектов и их совокупностей — естественный (или даже единственно возможный) способ организации нашего мышления, поэтому неудивительно, что он лежит в основе главного инструмента описания точного знания — математики.
Можно сказать, что множество — это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различны и отличимые друг от друга. Примерами множеств могут быть: множество людей, животных, растений на нашей планете, а также множество N натуральных чисел 1, 2, 3, ..., множество Р простых чисел 2, 3, 5, 7, 11, ... Множество Z целых чисел: ... , -2, -1, 0, 1, 2, ..., множество R вещественных чисел и т.д. Множество, не содержащее элементов, называется пустым. Обозначение: Æ. Пустое множество является подмножеством любого множества. Мощность пустого множества равна нулю. Понятие пустого множества (подобно понятию «нуль») возникает из потребности, чтобы результат всякой операции над множествами был также множеством.
Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U, которое называется универсальным множеством (или универсумом).
Если объект х является элементом множества М, то говорят, что х принадлежит М. Обозначение: хÎМ. В противном случае говорят, что х не принадлежит М. Обозначение: хÏМ. Заметим, что элементы множества сами могут являться множествами. Например, множество групп студентов состоит из элементов (групп), которые, в свою очередь, состоят из студентов.
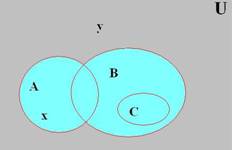
Рис 1.1.1
Пусть даны два множества А и В (рис 1.1.1), тогда:
- xÎA;
- yÏA и yÏB;
Подмножество – понятие части в теории множеств. Множество C является подмножеством множества B (рис. 1.1.1, обозначается CÌB) в случае, если каждый элемент множества C является также и элементом множества B. Например, множество всех чётных чисел является подмножеством множества всех целых чисел. Если C является подмножеством B, то B называется надмножеством C.
Обычно множества обозначают прописными буквами латинского алфавита, а элементы множеств — строчными буквами.
Понятия множества, элемента и принадлежности, которые на первый взгляд представляются интуитивно ясными, при ближайшем рассмотрении такую ясность утрачивают. Во-первых, проблематична отличимость элементов. Например, символы «е» и «а», которые встречаются на этой странице, — это один элемент множества А или два разных элемента? Во-вторых, проблематична возможность (без дополнительных усилий) указать, принадлежит ли данный элемент данному множеству. Например, является ли число 86958476921537485067857467 простым?
Множества, как объекты, могут быть элементами других множеств. Множество, элементами которого являются множества, обычно называется классом или семейством.
Семейства множеств обычно обозначают прописными «рукописными» буквами латинского алфавита, чтобы отличить их от множеств, не содержащих множеств в качестве элементов.
Похожие работы
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... , почему именно эти аксиомы оказались настолько успешными и достойными специального внимания. Соответственно самая большая слабость формализма состоит в невозможности объяснить, почему аксиомы теории множеств, предположительно не отражающие никакой реальности, способны доказывать арифметические утверждения, не доказуемые с помощью более финитистских средств. Слабость, которую, как я полагаю, ...
... вующий класс (предложение 4), то из аксиомы S следует, что для любого множества х класс всех его элементов, удовлетворяющих данной предикативной формуле A(у), есть множество. Однако для полного развития теории множеств потребуется аксиома, более сильная, чем аксиома S. Введем предварительно несколько определений. Определения Un (X) означает xyz ( X & X y = z). (X однозначен.) ...
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...
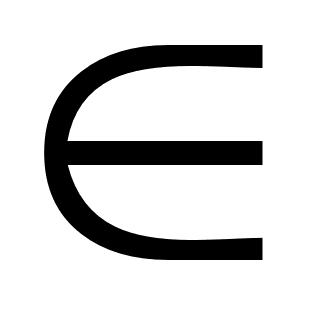
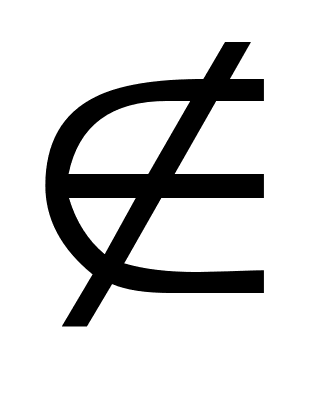
0 комментариев