Навигация
1. Аксиома выбора.
Для любого непустого множества А существует такое отображение j: Р(А) \ {Æ} ®A, что j (Х) Î X |для всех X Í А, X ¹ Æ.
2. Принцип полного упорядочения. Для любого непустого множества А существует бинарное отношение £ на А, для которого {A, £} вполне упорядоченное множество.
В системе ZFC справедлив принцип трансфинитной индукции, являющийся обобщением принципа полной индукции: если {A, £} - вполне упорядоченное множество, Р(х) — некоторое свойство, то справедливость свойства Р(х) на всех элементах х Î А следует из того, что для любого z Î А выполнимость свойства Р на элементах у, где у < z, влечет выполнимость P(z):
Глава 4. Представление множеств в ЭВМ
Термин «представление» (еще употребляют термин «реализация») применительно к программированию означает следующее. Задать представление какого-либо объекта (в данном случае множества) — значит описать в терминах используемой системы программирования структуру данных, используемую для хранения информации о представляемом объекте, и алгоритмы над выбранными структурами данных, которые реализуют присущие данному объекту операции. В данной работе предполагается, что в используемой системе программирования доступны такие общеупотребительные структуры данных, как массивы, структуры (или записи) и указатели. Таким образом, применительно к множествам определение представления подразумевает описание способа хранения информации о принадлежности элементов множеству и описание алгоритмов для вычисления объединения, пересечения и других введенных операций.
Следует подчеркнуть, что, как правило, один и тот же объект может быть представлен многими разными способами, причем нельзя указать способ, который является наилучшим для всех возможных случаев. В одних случаях выгодно использовать одно представление, а в других — другое. Выбор представления зависит от целого ряда факторов: особенностей представляемого объекта, состава и относительной частоты использования операций в конкретной задаче и т. д. Умение выбрать наиболее подходящее для данного случая представление является основой искусства практического программирования. Хороший программист отличается тем, что он знает много разных способов представления и умело выбирает наиболее подходящий.
4.1 Реализация операций над подмножествами заданного универсума U
Пусть универсум U – конечный, и число элементов в нём превосходит разрядности ЭВМ: | U | < n. Элементы универсума нумеруются: U = {u1… un}. Подмножество А универсума U представляется кодом (машинным словом или битовой шкалой) С, в котором
![]() 1, если u1ÎА
1, если u1ÎА
С[i] =
0, если unÏА
где С[i] – это i-й разряд кода С;
Код пересечения множеств А и В есть поразрядное логическое произведение кода множества А и кода множества В. Код объединения множеств А и В есть поразрядная логическая сумма кода множества А и кода множества В. В большинстве ЭВМ для этих операций есть соответствующие машинные команды. Таким образом, операции над небольшими множествами выполняются весьма эффективно. Если мощность универсума превосходит размер машинного слова, но не очень велика, то для представления множеств используются массивы битовых шкал. В этом случае операции над множествами реализуются с помощью циклов по элементам массива.
4.2 Генерация всех подмножеств универсума
Во многих переборных алгоритмах требуется последовательно рассмотреть все подмножества заданного множества. В большинстве компьютеров целые числа представляются кодами в двоичной системе счисления, причём число 2k – 1 представляется кодом, содержащим k единиц. Таким образом, число 0 является представлением пустого множества Æ, число 1 является представлением подмножества, состоящего из первого элемента, и т.д. Следующий тривиальный алгоритм перечисляет все подмножества n-элементного множества.
Алгоритм генерации всех подмножеств n-элементного множества:
Вход: n ³ 0 – мощность множества;
Выход: последовательность кодов подмножеств i;
for i from 0 to 2n – 1;
yield i;
end for;
Алгоритм выдаёт 2n различных целых чисел, следовательно, 2n различных кодов. С увеличением числа увеличивается количество двоичных разрядов, необходимых для его представления. Самое большое (из генерируемых) число 2n – 1 требует своего представления ровно n разрядов. Таким образом, все подмножества генерируются, причём ровно по одному разу. Недостаток этого алгоритма состоит в том, что порядок генерации подмножеств никак не связан с их составом. Например, вслед за подмножеством с кодом 0111 будет перечислено подмножество с кодом 1000.
4.3 Представление множеств упорядоченными списками
Если универсум очень велик (или бесконечен), а рассматриваемые подмножества универсума не очень велики, то представление с помощью битовых шкал не является эффективным с точки зрения экономии памяти. В этом случае множества представляются записью с двумя полями: информационным и указателем на следующий элемент. Весь список представляется указателем на первый элемент.
elem = record;
i: info; {информационное поле};
n: n {указатель на следующий элемент};
end record;
При таком представлении трудоёмкость операции Î составит О(n), а трудоёмкость операций Ì, Ç, È составит О(n×m), где n и m – мощности участвующих в операции множеств.
Если элементы в списках упорядочить, например, по возрастанию значения поля i, то трудоёмкость всех операций составит О(n). Эффективная реализация операций над множествами, представленными в виде упорядоченных списков, основана на весьма общем алгоритме, известном как алгоритм слияния. Алгоритм типа слияния параллельно просматривает два множества, представленных упорядоченными списками, причём на каждом шаге продвижение происходит в том множестве, в котором текущий элемент меньше.
Заключение
Курсовой проект выполнен на тему «Элементы теории множеств». В нём рассмотрены вопросы:
- Множества: элементы и множества, способы задания множеств, количество элементов в множестве;
- Операции над множествами: сравнение множеств, основные операции над множествами, свойства операций над множествами;
- Аксиоматическая теория множеств: наивная теория множеств, аксиомы теории множеств;
- Представление множеств в ЭВМ: Реализация операций над подмножествами заданного универсума U, Генерация всех подмножеств универсума, Представление множеств упорядоченными списками;
На основании найденной информации (учебная литература, Internet), я выделил основные пункты, которые наиболее полно и точно дают представление о теории множеств. При выполнении работы были приведены примеры множеств, а также и те примеры, которые приводят к противоречиям при различном способе их задания. При исследовании свойств операций над множествами я доказал одно из свойств (дистрибутивность) с помощью диаграмм Эйлера-Венна. И я считаю, что в последней главе необходимо было указать на связь между множествами и их представлением на ЭВМ, особенно это важно, на мой взгляд, для специальности математика-программиста.
После проделанной работы можно сделать следующий вывод:
Понятия «множества» и «элементы множеств» составляет основной словарь математической логики. Именно эти понятия закладывают основу, которая необходима для дальнейших построений.
Список использованной литературы
1. Дискретная математика для программистов / Ф.А.Новиков. – СПб.: Питер, 2002. – 304 с.
2. Жолков С.Ю. Математика и информатика для гуманитариев: Учебник. – М.: Гардарики, 2002. – 531 с.
3. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики: Учебник. – М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2002. – 280 с. – (Серия «Высшее образование»)
4. Шипачёв В.С. Высшая математика. Учеб. Для вузов. – 4-е изд., стер. – М.: Высшая школа. 1998. – 479 с.
5. Материал из Википедии — свободной энциклопедии. Георг Кантор (http://www.peoples.ru/science/mathematics/kantor/)
Похожие работы
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... , почему именно эти аксиомы оказались настолько успешными и достойными специального внимания. Соответственно самая большая слабость формализма состоит в невозможности объяснить, почему аксиомы теории множеств, предположительно не отражающие никакой реальности, способны доказывать арифметические утверждения, не доказуемые с помощью более финитистских средств. Слабость, которую, как я полагаю, ...
... вующий класс (предложение 4), то из аксиомы S следует, что для любого множества х класс всех его элементов, удовлетворяющих данной предикативной формуле A(у), есть множество. Однако для полного развития теории множеств потребуется аксиома, более сильная, чем аксиома S. Введем предварительно несколько определений. Определения Un (X) означает xyz ( X & X y = z). (X однозначен.) ...
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...
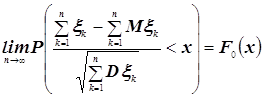
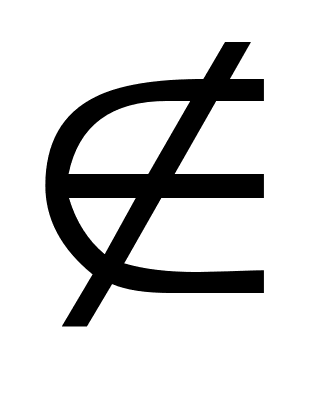
0 комментариев