Навигация
2.1 Сравнение множеств
множество элемент аксиоматический принадлежность
Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент B:
![]() .
.
Если ![]() и
и ![]() , то A называется собственным подмножеством В. Заметим, что
, то A называется собственным подмножеством В. Заметим, что ![]() . По определению
. По определению ![]() .
.
Два множества называются равными, если они являются подмножествами друг друга: ![]()
Теорема о сравнении множеств. Для любых множеств A и B существует одна и только одна из следующих возможностей: |A| = |B|, |A| < |B|, |A| > |B|.
2.2 Основные операции над множествами
Ниже перечислены основные операции над множествами:
· объединение:
![]()
· пересечение:
![]()
· разность:
![]()
· симметрическая разность:
![]()
· дополнение:
![]()
Операция дополнения подразумевает некоторый универсум (множество U, которое содержит A): ![]()
Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Объединением двух множеств A È B (рис. 2.2.1) – называется третье множество, каждый элемент которого принадлежит хотя бы одному из множеств A и B
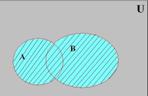
Рис. 2.2.1
Пересечением множеств А∩В (рис 2.2.2), является множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам.
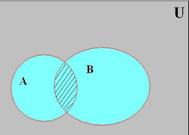
Рис 2.2.2
Разностью множеств A \ B = A – B (рис. 2.2.3) – называется такое множество, каждый элемент которого принадлежит множеству A, но не принадлежит множеству B.
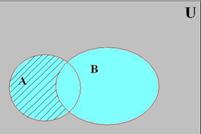
Рис. 2.2.3
Симметрическая разность A D B (рис. 2.2.4)
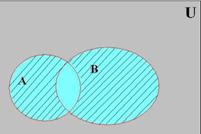
Рис. 2.2.4
Дополнение к множеству A называется множество всех элементов, не входящих в множество A (рис 3.2.5)
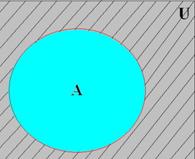
Рис. 2.2.5
2.3 Свойства операций над множествами
Пусть задан универсум U. Тогда для всех A,B,C Ì U выполняются следующие свойства (табл. 2.3.1):
Свойства операций над множествами
| Для объединения ( È ) | Для пересечения ( Ç ) |
| Идемпотентность | |
| A È A = A | A Ç A =A |
| Коммутативность | |
| A È B = B È A | A Ç B = B Ç A |
| Ассоциативность | |
| A È (B È C) = (A È B) È C | A Ç (B Ç C) = (A Ç B) Ç C |
| Дистрибутивность | |
| A È (B Ç C) = (A È B) Ç (A È C) | A Ç (B È C) = (A Ç B) È (A Ç C) |
| Поглощение | |
| (A Ç B) È A = A | (A È B) Ç A = A |
| Свойства нуля | |
| A È Æ = A | A Ç Æ = Æ |
| Свойства единицы | |
| A È U = U | A Ç U = U |
| Инволютивность | |
|
| |
| Законы де Моргана | |
|
|
|
| Свойства дополнения | |
|
|
|
| Выражение для разности | |
|
| |
| Выражение для симметрической разности | |
|
| |
В справедливости перечисленных свойств можно убедиться различными способами. Например, нарисовать диаграммы Эйлера для левой и правой частей равенства и убедиться, что они совпадают, или же провести формальное рассуждение для каждого равенства. Рассмотрим для примера первое равенство: A È A = А. Возьмем произвольный элемент х, принадлежащий левой части равенства, х Î A È A. По определению операции объединения È имеем хÎ A È хÎ A. В любом случае хÎ A. Взяв произвольный элемент из множества в левой части равенства, обнаружили, что он принадлежит множеству в правой части. Отсюда по определению включения множеств получаем, что A È A Ì А. Пусть теперь хÎ A. Тогда, очевидно, верно хÎ A È хÎ A. Отсюда по определению операции объединения имеем х Î A È A. Таким образом, А Ì A È A. Следовательно, по определению равенства множеств, A È A = А. Аналогичные рассуждения нетрудно провести и для остальных равенств.
Докажем свойство дистрибутивности для операции объединения на диаграммах Эйлера-Венна (рис 2.3.1):
A È (B Ç C) = (A È B) Ç (A È C)
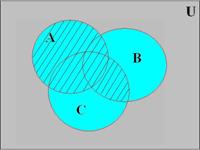
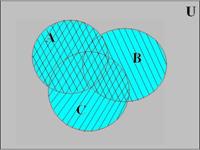
Рис. 2.3.1
Глава 3. Аксиоматическая теория множеств
Похожие работы
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... , почему именно эти аксиомы оказались настолько успешными и достойными специального внимания. Соответственно самая большая слабость формализма состоит в невозможности объяснить, почему аксиомы теории множеств, предположительно не отражающие никакой реальности, способны доказывать арифметические утверждения, не доказуемые с помощью более финитистских средств. Слабость, которую, как я полагаю, ...
... вующий класс (предложение 4), то из аксиомы S следует, что для любого множества х класс всех его элементов, удовлетворяющих данной предикативной формуле A(у), есть множество. Однако для полного развития теории множеств потребуется аксиома, более сильная, чем аксиома S. Введем предварительно несколько определений. Определения Un (X) означает xyz ( X & X y = z). (X однозначен.) ...
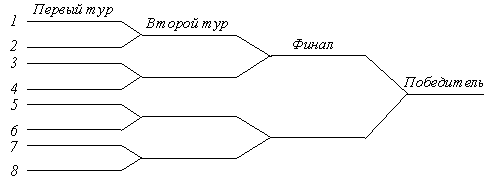
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...
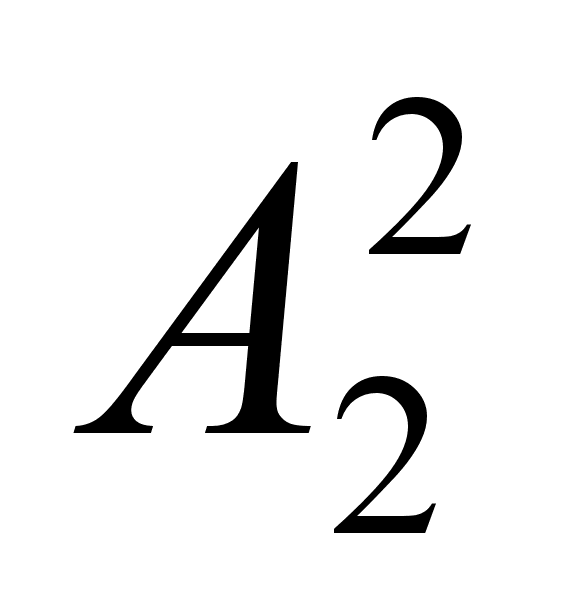
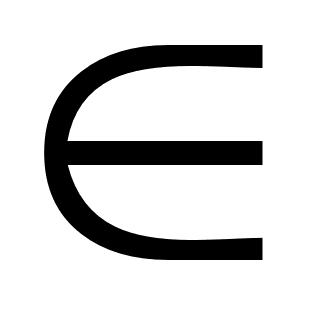
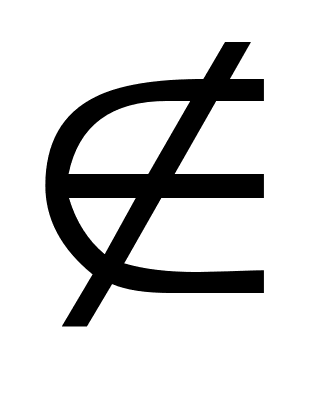
0 комментариев