Середні величини

2.3 Середні величини

Середня величина – це узагальнюючі показник, які характеризують рівень варіруючої ознаки в якісно однорідній сукупності.

Сукупність, яку ми збираємося характеризувати середньою величиною повинна бути:

1) якісно однорідною, однотипною;

2) складатися з багатьох одиниць.

Середні величини можуть бути абсолютними або відносними залежно від вихідної бази.

Середні можуть бути прості і зважені.

Найбільш простим видом середніх величин є середньоарифметична проста

Найбільш простим видом середніх величин є середньоарифметична проста:

,

де n – кількість одиниць сукупності,

x – варіруюча ознака.

Вона застосовується в тому випадку, коли у нас варіююча арифметична ознака має різні значення, і є незгруповані дані.

Якщо ж ми маємо згруповані дані, або варіруюча ознака зустрічається декілька раз, то застосовується середня арифметична зважена.

,

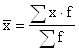де x – варіруюча ознака,

f – абсолютна кількість повторення варіруючої ознаки.

Середня гармонічна – це обернена величина до середньої арифметичної, обчислена з обернених величин осереднюваних варіруючих ознак.

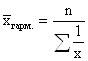
Середня геометрична розраховується за формулою:

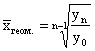
Середні поділяються на 2 великі класи: структурні і степеневі (сюди належать середня гармонічна, середня геометрична, середня квадратична, середня прогресивна тощо).

Середню арифметичну зважену обчислюють за формулою:

,

де f₁, f₂,.. – частоти.

За способом моментів середню арифметичну обчислюють за формулою:

,

де А- умовний нуль.

За умовний нуль доцільно приймати варіанту, яка знаходиться в центрі ряду розподілу або варіанту, якій відповідає найбільша частота.

Мода – це та варіанта, що найчастіше повторюється в ряді розподілу.

В дискретному варіаційному ряді моду легко відшукати візуально, бо це варіанта, якій відповідає найбільша частота.

В інтервальному ряді моду визначають за допомогою додаткових розрахунків. Спочатку обчислюють модальний інтервал, тобто інтервал, який має найбільшу частоту. Після цього мода визначається за формулою:

де Mo—мода; X_{Mo min} — нижня межа модального інтервалу; і— величина модального інтервалу; n_Mo — частота модального інтервалу; n_Mo-1 — частота інтервалу перед модальним; n_Mo+1 — частота інтервалу після модального.

Медіана – це варіанта, що ділить ранжирований ряд на дві рівні частини. Якщо непарне число варіант записати в порядку зростання чи спадання, то центральна з них і буде медіаною. Коли число варіант парне, медіана розраховується як середня арифметична двох центральних варіант.

При визначенні медіани за даними ряду розподілу використовують кумулятивні частоти, які полегшують пошук центральної варіанти.

В інтервальному ряді розподілу аналогічно визначається медіанний інтервал. Значення медіани обчислюється за формулою

 

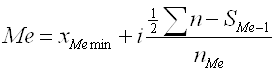
де X_{Me min} — нижня межа медіанного інтервалу; і — величина медіанного інтервалу; n_Me — частота медіанного інтервалу; S_Me-1 —сума нагромаджених частот перед медіанним інтервалом.

Розрахункова частина до підрозділу 2.3:

До кожного ряду обчислити показники:

1.  середня зважена

2.  середня способом моментів

3.  мода

4.  медіана

1. Результативна ознака (реалізація яєць, млн. шт.):

Дані для побудови таблиці беремо з розрахунків підпункту 2.1:

S_f – кумулятивна частота визначається як

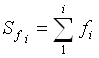
Частку визначимо як:

 

Кумулятивна частка визначається як:

 

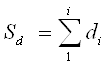
В результаті підрахунків і групування отримуємо таблицю для ряду розподілу результативної ознаки (реалізація яєць,тис. грн.):

Таблиця 5

Результати групування для результативної ознаки

Реалізація збуту яєць,тис. грн.	Середнє значення інтервалу	Кількість областей, частота fi	Кумулятивна частота, Sf	Звичайна частка, d	Кумулятивна частка, Sd
207,27-145089,02	72648,15	22	22	88	88
145089,03-289970,78	217529,91	2	24	8	96
289970,79-434852,54	362411,67	1	25	4	100
Всього	х	25	Х	100	Х

1.  Середню величину визначимо за допомогою формул:

- середньої зваженої:

,

де  – середнє значення факторної ознаки в і-му інтервалі;

f_i – частота і-го інтервалу.

Порахуємо:

 грн.

- середня за способом моментів визначається як:

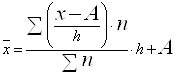
де А - величина, взята за початок відліку;

h – крок інтервалу.

Для розрахунків всі обчислення занесемо в таблицю:

Таблиця 6

Групування для розрахунків

Реалізація збуту яєць,тис. грн	Середнє значення інтервалу	Кількість областей, частота fi	h*x
207,27-145089,02	72648,15	22	1598259,19	-0,01	0,00	0,00
145089,03-289970,78	217529,91	2	435059,81	144881,76	1,00	2,00
289970,79-434852,54	362411,67	1	362411,67	289763,52	2,00	2,00
Всього	х	25	2395730,67	434645,27	3,00	4,00

Величину за початок відліку візьмемо А=72648,15 тис. грн.

 тис. грн.

2.  Мода:

,

де x_min та h – відповідно нижня межа та ширина модального інтервалу; - частоти модального, передмодального та післямодального інтервалу.

Підставляючи у формулу, маємо:

 тис. грн.

3. Медіана:

,

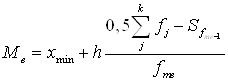де f_me – частота медіанного інтервалу;

S_fme-1 – кумулятивна частота передмедіанного інтервалу.

В інтервальному ряді медіанним буде значення ознаки, для якої кумулятивна частота перевищує або дорівнює половині обсягу сукупності.

Підставивши у формулу, маємо:

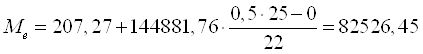 тис. грн.

3.  За факторною ознакою (кількість, млн. шт):

Таблиця 7

Результати групування для факторної ознаки

Кількість, млн. шт.	Середнє значення інтервалу	Кількість областей, частота fi	Кумулятивна частота, Sf	Звичайна частка, d	Кумулятивна частка, Sd
0,7-255,98	128,34	15	15	60	15
255,99-511,27	383,63	7	22	28	22
511,28-766,56	638,92	1	23	4	23
766,57-1021,85	894,21	1	24	4	24
1021,86-1277,14	1149,50	1	25	4	25
Всього	х	25	х	100	Х

4.  Середню величину визначимо за допомогою формул:

- середньої зваженої:

,

де  – середнє значення факторної ознаки в і-му інтервалі;

f_i – частота і-го інтервалу.

Порахуємо:

млн. шт.

- середня за способом моментів визначається як:

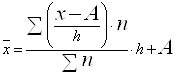
де А - величина, взята за початок відліку;

h – крок інтервалу.

Для розрахунків всі обчислення занесемо в таблицю:

Таблиця 8

Групування для розрахунків

Кількість, млн. шт.	Середнє значення інтервалу	Кількість областей, частота fi	h*x
0,7-255,98	128,34	15	1925,10	0,00	0,00	0,00
255,99-511,27	383,63	7	2685,41	255,29	1,00	7,00
511,28-766,56	638,92	1	638,92	510,58	2,00	2,00
766,57-1021,85	894,21	1	894,21	765,87	3,00	3,00
1021,86-1277,14	1149,50	1	1149,50	1021,16	4,00	4,00
Всього	х	25	7293,14	2552,90	10,00	16,00

Величину за початок відліку візьмемо А=128,34 млн. шт.

млн. шт.

2. Мода:

,

де x_min та h – відповідно нижня межа та ширина модального інтервалу; - частоти модального, передмодального та післямодального інтервалу.

Підставляючи у формулу, маємо:

млн.шт.

4.  Медіана:

,

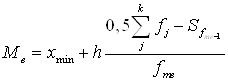де f_me – частота медіанного інтервалу;

S_fme-1 – кумулятивна частота передмедіанного інтервалу.

В інтервальному ряді медіанним буде значення ознаки, для якої кумулятивна частота перевищує або дорівнює половині обсягу сукупності.

Підставивши у формулу, маємо:

 млн. шт.

3. За факторною ознакою (ціна за тисячу штук, грн.):

Таблиця 9

Результати групування для факторної ознаки

Ціна за тисячу, грн.	Середнє значення інтервалу	Кількість областей, частота fi	Кумулятивна частота, Sf	Звичайна частка, d	Кумулятивна частка, Sd
226,1-248,98	237,54	5	5	20	20
248,99-271.87	260,43	12	17	48	68
271,88-294,76	283,32	2	19	8	76
294,77-317,65	306,21	5	24	20	96
317,66-340,54	329,10	1	25	4	100
Всього	х	25	х	100	Х

1.  Середню величину визначимо за допомогою формул:

 

- середньої зваженої:

,

де  – середнє значення факторної ознаки в і-му інтервалі;

f_i – частота і-го інтервалу.

Порахуємо:

грн.

- середня за способом моментів визначається як:

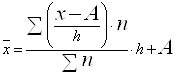
де А - величина, взята за початок відліку;

h – крок інтервалу.

Для розрахунків всі обчислення занесемо в таблицю:

Таблиця 10

Групування для розрахунків

Ціна за тисячу штук, грн	Середнє значення інтервалу	Кількість областей, частота fi	h*x
226,1-248,98	237,54	5	1187,70	-22,89	-1,00	-5,00
248,99-271.87	260,43	12	3125,16	0,00	0,00	0,00
271,88-294,76	283,32	2	566,64	22,89	1,00	2,00
294,77-317,65	306,21	5	1531,05	45,78	2,00	10,00
317,66-340,54	329,10	1	329,10	68,67	3,00	3,00
Всього	х	25	6739,65	114,45	5,00	10,00

Величину за початок відліку візьмемо А=260,43 грн.

грн.

2. Мода:

,

де x_min та h – відповідно нижня межа та ширина модального інтервалу; - частоти модального, передмодального та післямодального інтервалу.

Підставляючи у формулу, маємо:

грн.

3. Медіана:

,

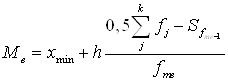де f_me – частота медіанного інтервалу;

S_fme-1 – кумулятивна частота передмедіанного інтервалу.

В інтервальному ряді медіанним буде значення ознаки, для якої кумулятивна частота перевищує або дорівнює половині обсягу сукупності.

Підставивши у формулу, маємо:

 грн.

2.4.Варіація ознак та показники їх вимірювання

Середня величина являє собою узагальнюючу статистичну характеристику, в якій отримує кількісний вираз типовий рівень ознаки, якою володіють члени досліджуваної сукупності. Проте однією середньою величиною неможливо відобразити всі характерні риси статистичного розподілу, тому використовують показники варіації для впорядкування статистичних сукупностей.

Розмах варіації (R) — це різниця між найбільшим і найменшим значеннями ознаки:

Середнє лінійне відхилення (l) (розраховують без урахування знаків):

де x — індивідуальне значення ознаки (варіанта); x — середнє значення ознаки; n — кількість варіант; f — частота.

Середній квадрат відхилення (σ²) — дисперсія:

Середнє квадратичне відхилення (σ):

Коефіцієнт варіації (використовують при порівнюванні варіації однієї і тієї ж ознаки в різних сукупностях):

Розрахунки до підпункту 2.4:

1. Результативна ознака (реалізація яєць, тис. грн.):

Таблиця 11

Результати групування для результативної ознаки

Реалізація яєць, тис. грн	Середнє значення інтервалу	Кількість областей, частота fi
207,27-145089,02	72648,15	22	23181,08	509983,80	537362544,15	11821975971,21
145089,03-289970,78	217529,91	2	121700,68	243401,36	14811055123,02	29622110246,04
289970,79-434852,54	362411,67	1	266582,44	266582,44	71066196463,29	71066196463,29
Всього	х	25	411464,20	1019967,59	86414614130,46	112510282680,54

1.  Розмах варіації:

R = 434852,54-207,27=434645,28 тис. грн.

2.  Середнє лінійне відхилення:

d= ∑ / ∑f_i=1019967,59/25=40798,70 тис. грн.

3.  Дисперсія:

σ² =( ∑( )²f_i ) / ∑f_i =112510282680,54/25=4500411307,22 тис. грн.

4.  Середньоквадратичне відхилення:

σ = √ 4500411307,22 =67085,10 тис. грн.

5. Коефіцієнт варіації квадратичний:

V_s = (67085,10/ 95829,23)*100% = 70,00%.

2.  За факторною ознакою (кількість, млн. шт.):

 

Таблиця 12

Результати групування для факторної ознаки

Кількість, млн. шт.	Середнє значення інтервалу	Кількість областей, частота fi
0,7-255,98	128,34	15	163,39	2450,78	26694,85	400422,81
255,99-511,27	383,63	7	91,90	643,33	8446,42	59124,93
511,28-766,56	638,92	1	347,19	347,19	120543,95	120543,95
766,57-1021,85	894,21	1	602,48	602,48	362987,45	362987,45
1021,86-1277,14	1149,50	1	857,77	857,77	735776,92	735776,92
Всього	х	25	2062,74	4901,57	1254449,60	1678856,07

1.  Розмах варіації:

R = 1277,14-0,7=1276,40 млн. шт.

2.  Середнє лінійне відхилення:

d= 4901,57/25=196,06 млн. шт.

3.  Дисперсія:

σ² =1678856,07/25=67154,24 млн. шт.

4. Середньоквадратичне відхилення:

σ = √ 67154,24=259,14 млн. шт.

5. Коефіцієнт варіації квадратичний:

V_s = (259,14/ 291,73)*100% = 88,83%.

3.  За факторною ознакою (ціна за тисячу штук, грн.):

Ціна за тисячу штук, грн.	Середнє значення інтервалу	Кількість областей, частота fi
226,1-248,98	237,54	5	32,05	160,23	1026,95	5134,73
248,99-271.87	260,43	12	9,16	109,87	83,83	1005,99
271,88-294,76	283,32	2	13,73	27,47	188,62	377,25
294,77-317,65	306,21	5	36,62	183,12	1341,32	6706,59
317,66-340,54	329,10	1	59,51	59,51	3541,92	3541,92
Всього	х	25	151,07	540,20	6182,63	16766,47

 

Таблиця 13

Результати групування для факторної ознаки

1.  Розмах варіації:

R = 340,54-226,1=114,40 грн.

2.  Середнє лінійне відхилення:

d= 540,20/25=21,61 грн.

3.  Дисперсія:

σ² =16766,47/25=670,66 грн.

4. Середньоквадратичне відхилення:

σ = √ 670,66=25,90 грн.

5. Коефіцієнт варіації квадратичний:

V_s = (25,90/ 269,59)*100% = 9,61%.

Розділ III. Кореляційний аналіз реалізації худоби і птиці та чинники, що її формують

Кореляційний зв'язок — такий зв'язок між ознаками суспільно-економічних явищ, при якому на величину результативної ознаки, крім факторної, впливають багато інших ознак, що діють у різних напрямах одночасно або послідовно. Під терміном «кореляційний зв'язок» розуміють неповний статистичний або частковий зв'язок. Його особливістю є те, що кожному значенню факторної ознаки відповідає не одне певне значення результативної, а ціла їх сукупність. Тобто для встановлення зв'язку необхідно знайти середнє значення результативної ознаки для кожного значення факторної. Практичний аспект виміру кореляційного-зв'язку має на меті, і одного боку, визначення форми зв'язку, з другого— встановлення його тісноти.