Навигация
Перевод неправильных дробей
2.3 Перевод неправильных дробей
При переводе неправильной дроби необходимо отдельно перевести целую и дробную части по вышеизложенным правилам и записать число в новой системе счисления, оставив неизменным положение запятой.
2.4 Перевод чисел из системы счисления в систему с кратным основанием
Если основания систем счисления кратны друг другу, т.е. связаны зависимостью: l=pm, то каждая цифра системы счисления с основанием l может быть представлена m цифрами в системе с основанием p.
Следовательно, для того, чтобы перевести число из исходной системы в новую, основание которой кратно основанию исходной системы, достаточно каждую цифру переводимого числа записать при помощи m цифр в новой системе счисления, если основание исходной системы больше основания новой системы счисления. В противном случае каждые m цифр исходного числа необходимо записать при помощи одной цифры в новой системе счисления, начиная для целых чисел с младшего разряда и для правильных дробей - со старшего.
Пример.
[0,536]10=[0,100’010’010]2=[0,422]8 ; [0,1000’1001’0]2=[0,89]16
[138]10=[10’001’010]2=[212]8: [1000’1010]2=[8А]16
3. Выбор системы счисления для применения в ЭВМ
Очевидно, что непозиционные системы счисления непригодны для применения в ЭВМ в силу своей громоздкости и трудности выполнения арифметических операций.
Из позиционных наиболее удобны однородные. С точки зрения применения в ЭВМ учитываются следующие факторы.
1. Наличие физических элементов, способных изобразить символы системы.
2. Экономичность системы, т.е. количество элементов необходимое для представления многоразрядных чисел.
3. Трудоемкость выполнения арифметических операций в ЭВМ.
4. Быстродействие вычислительных систем.
5. Наличие формального математического аппарата для анализа и синтеза вычислительных устройств.
6. Удобство работы человека с машиной.
7. Помехоустойчивость кодирования цифр на носителях информации.
Исторически сложилось так, что для применения в ЭВМ была выбрана двоичная система счисления, которая наиболее полно соответствует этим критериям.
В современных универсальных ЭВМ применяются как двоичная, так и десятичная системы счисления. Причем цифры последней кодируются двоичными символами, т. е. речь идет в действительности не о десятичной, а о двоично-десятичной системе счисления. Каждая из отмеченных систем имеет свои достоинства и недостатки, а также свои области применения.
Достоинствами двоичной системы счисления относительно двоично-десятичной являются:
1) экономия порядка 20 % оборудования;
2) примерно в 1,5 раза более высокое быстродействие;
3) упрощение логического построения и значительная экономия оборудования в схемах управления и во вспомогательных цепях.
Достоинствами двоично-десятичной системы являются:
1) отсутствие необходимости перевода исходных данных и результатов расчетов из одной системы в другую;
2) удобство контроля промежуточных результатов путем вывода их на индикацию для визуального наблюдения;
3) более широкие возможности для автоматического контроля из-за наличия в двоично-десятичном коде избыточных комбинаций.
Двоичную систему счисления применяют в больших и средних ЭВМ, предназначенных для решения научно-технических задач, для которых характерен большой объем вычислений и сравнительно малый объем исходных данных и результатов вычислений. Ее также целесообразно применять в ЭВМ, предназначенных для управления технологическими процессами.
Двоично-десятичную систему счисления применяют для решения экономических задач, которые характеризуются большим объемом исходных данных, сравнительной простотой и малым объемом выполняемых над ними преобразований и большим количеством результатов вычислений. Эту систему целесообразно также применять в калькуляторах, ЭВМ, предназначенных для инженерных расчетов, а также в персональных ЭВМ.
4. Двоичная система счисления
Под двоичной системой счисления понимается такая система, в которой для изображения чисел используются два символа, а веса разрядов меняются по закону 2+-к, где к - произвольное целое число. Классической двоичной системой является система с символами 0, 1. Ее двоичные цифры часто называют битами. В общем виде все двоичные числа представляются в виде:
А= ∑аі2і, (і от -к до n)
Чтобы овладеть любой системой счисления, надо уметь выполнять в ней арифметические операции. Арифметические операции в двоичной системе счисления выполняются так же, как и в десятичной в соответствии с таблицами поразрядных вычислений.
Сложение в двоичной системе счисления производится по правилам сложения полиномов. Поэтому при сложении чисел А и В i-й разряд суммы Siи перенос Пiиз данного разряда в (i+1) разряд будет определяться в соответствии со следующим выражением:
аі+ bі + Пі-1= Sі +Пі+1
| аі | bі | Пі-1 | Sі | Пі+1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Таблица умножения двух двоичных чисел полностью определяется двумя правилами:
- умножение любого числа на ноль дает в результате ноль,
- умножение любого числа на 1 оставляет его без изменения, т.е. результат равен исходному числу.
Похожие работы
... 100 10 1001=(9)10 100 11,1=(3,5)10 00 110 00 100 001 100 000 100 10 0 10 00 Таким образом, выполнение арифметических операций в двоичной системе счисления достаточно просто. Особенно просто выполнять операции сложения, вычитания и умножения. Благодоря этому, применение двоичной системы в вычислительных ...
... посылали гонцов, использовали почтовых голубей. У народов существовали различные способы оповещения о надвигающейся опасности: барабанный бой, дым костров, флаги и т. д. Однако использование такого представления информации требует предварительной договоренности о понимании принимаемого сообщения. Знаменитый немецкий ученый Готфрид Вильгельм Лейбниц предложил еще в XVII веке уникальную и простую ...
... будут происходить в будущих общеобразовательных и других учебных заведениях. Я не ставила перед собой цель оценивать эти сложные процессы, но нужно сделать вывод, что стремление обеспечивать личностно – ориентированное обучение на уроках информатики, создавать условия для развития индивидуальности ученика это важная, если не самая главная задача учителя. Хотя она и не из разряда легких. Именно ...
... быть выведены на печать. На экране рисунки могут быть статическими (неподвижными) или динамическими (движущимися). В последнее время машинная графика выделилась в самостоятельный раздел информатики с многочисленными приложениями. Средствами машинной графики создается не только печатная продукция, но и рекламные ролики на телевидении, мультфильмы. Объясним, как кодируется изображение в памяти ...




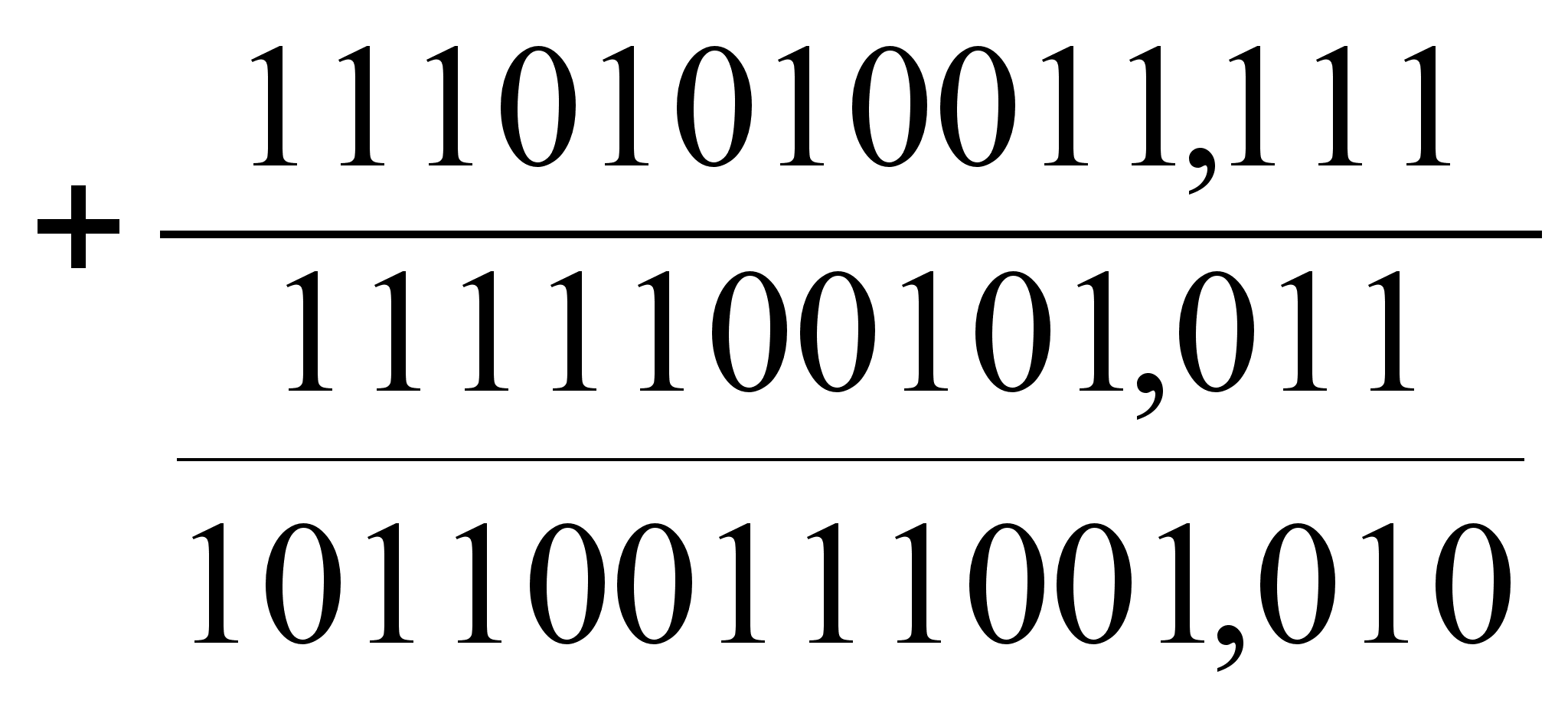


0 комментариев