Навигация
Точность представления чисел в ЭВМ
32294
знака
6
таблиц
4
изображения
6. Точность представления чисел в ЭВМ
При решении различных задач требуется различная точность получаемых результатов. Так, при решении инженерных задач достаточна точность до 3—4 десятичных знаков (10—13 двоичных), при решении научных задач — 5—6 десятичных или 16—20 двоичных знаков и при решении особо точных задач — до 50 двоичных разрядов.
При ограниченной длине машинных слов множество чисел, которые можно представить в машине, является конечным. Поэтому представление чисел в ЭВМ, как правило, влечет за собой появление погрешностей, величина которых зависит как от формы представления чисел, так и от длины разрядной сетки.
Точность представления числа характеризуется абсолютной и относительной погрешностями.
Абсолютная погрешность — это разность между истинным значением величины А и ее значением, полученным из машинного изображения [А], т. е.
Усредненная абсолютная погрешность представления чисел в машинах с фиксированной запятой определяется как среднее арифметическое между минимально представимым числом и его минимальной потерей, т. е.
В машинах с фиксированной запятой абсолютная погрешность постоянна и равна половине младшего разряда.
Относительная погрешность представления определяется как отношение усредненной абсолютной погрешности к самому числу:
.
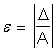Так как само число с фиксированной запятой меняется в пределах
,
то и относительная погрешность является величиной переменной, меняющейся соответственно в пределах
Для машин с фиксированной запятой она определяется следующим образом:
Таким образом, относительная погрешность для машин с фиксированной запятой зависит от величины числа и колеблется в пределах от 
для больших чисел, до 2-1 для малых чисел. В машинах с плавающей запятой абсолютная погрешность представления числа определяется следующим образом:
где 
- погрешность представления мантиссы, которая определяется так же, как абсолютная погрешность представления чисел в машине с фиксированной запятой, т. е. 
- порядок числа, который изменяется в пределах
.
Следовательно, в отличие от машин с фиксированной запятой, в машинах с плавающей запятой абсолютная погрешность представления чисел зависит от порядка числа: минимальная при наибольшем отрицательном m и максимальная при наибольшем положительном определяются следующим образом:
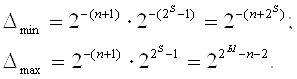
Относительная погрешность представления чисел в машинах с плавающей запятой определяется по общему правилу:
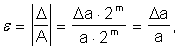
т. е. 
не зависит от порядка числа и изменяется в пределах
Следовательно, в машинах с плавающей запятой, в отличие от машины с фиксированной запятой, относительная погрешность изображения чисел во всем диапазоне представления практически постоянна и для чисел с нормализованной мантиссой зависит от количества разрядов мантиссы: чем их больше, тем меньше погрешность представления.
В некоторых вычислительных средствах информационной единицей являются не отдельные числа, а их блоки или массивы, т. е. последовательности, состоящие из сотен и тысяч чисел. В этих случаях нередко применяется промежуточная форма представления чисел в ЭВМ, так называемое представление с поблочно плавающей запятой, при котором всему массиву чисел присваивается общий порядок и массив считается нормализованным, если хотя бы одно его слово является нормализованным. Естественно, что относительная погрешность представления отдельных элементов массива будет при этом различной. Как и в случае представления с фиксированной запятой, максимальный по абсолютной величине элемент будет представлен с минимальной, в то время как минимальный по абсолютной величине элемент массива — с максимальной относительной погрешностью. Однако это не имеет существенного значения, так как основную информационную нагрузку в этих случаях несут максимальные элементы массивов. Вместе с тем благодаря представлению чисел с поблочно плавающей запятой удается при приемлемой точности вычислений значительно сократить объем оборудования, а главное - время выполнения операции, так как действия над порядками в этом случае выполняются только один раз за время обработки всего массива чисел.
Из этого следует, что нельзя отдать предпочтение какой-либо одной форме представления чисел. Обычно в ЭВМ общего назначения применяют нормальную форму. Этим обеспечивается большой диапазон представления чисел, высокая точность вычислений, простота программирования. Усложнение аппаратуры этих ЭВМ имеет второстепенное значение.
В специализированных ЭВМ чаще применяют фиксированную или поблочно плавающую запятую, если информация обрабатывается отдельными массивами, так как эти формы обеспечивают простоту конструкции ЭВМ. Диапазон изменения величин известен заранее, масштабные коэффициенты подбираются один раз, требуемая точность вычислений также известна заранее и определяет длину разрядной сетки.
В современных ЭВМ используются обе формы представления чисел. При этом в большинстве случаев формат чисел с фиксированной запятой служит для представления целых двоичных и десятичных чисел и выполнения операций над ними, что, например, необходимо для операций над кодами адресов (операции индексной арифметики).
Вывод
В процессе написания реферата мы ознакомились с:
- с понятием системы счисления;
- классификацией систем счисления;
- переводом чисел из одной системы счисления в другую;
- выбором системы счисления для применения в ЭВМ;
- двоичной системой счисления;
- формами представления двоичных чисел в ЭВМ;
- точностью представления чисел в ЭВМ и др.
Литература
1. Самофалов К.Г., Романкевич А.М., и др. Прикладная теория цифровых автоматов. - Киев. “Вища школа” 1987.
2. Соловьев Г.Н. Арифметические устройства ЭВМ. - М. “Энергия”. 1978.
3. Савельев А.Я. Прикладная теория цифровых автоматов - М. “Высшая школа”. 1987.
4. Каган Б.М. Электронные вычислительные машины и системы. - М. Энергоатомиздат. 1985.
5. Лысиков Б.Г. Арифметические и логические основы цифровых автоматов. - Минск. “Вышэйшая школа”. 1980.
Похожие работы
... 100 10 1001=(9)10 100 11,1=(3,5)10 00 110 00 100 001 100 000 100 10 0 10 00 Таким образом, выполнение арифметических операций в двоичной системе счисления достаточно просто. Особенно просто выполнять операции сложения, вычитания и умножения. Благодоря этому, применение двоичной системы в вычислительных ...
... посылали гонцов, использовали почтовых голубей. У народов существовали различные способы оповещения о надвигающейся опасности: барабанный бой, дым костров, флаги и т. д. Однако использование такого представления информации требует предварительной договоренности о понимании принимаемого сообщения. Знаменитый немецкий ученый Готфрид Вильгельм Лейбниц предложил еще в XVII веке уникальную и простую ...
... будут происходить в будущих общеобразовательных и других учебных заведениях. Я не ставила перед собой цель оценивать эти сложные процессы, но нужно сделать вывод, что стремление обеспечивать личностно – ориентированное обучение на уроках информатики, создавать условия для развития индивидуальности ученика это важная, если не самая главная задача учителя. Хотя она и не из разряда легких. Именно ...
... быть выведены на печать. На экране рисунки могут быть статическими (неподвижными) или динамическими (движущимися). В последнее время машинная графика выделилась в самостоятельный раздел информатики с многочисленными приложениями. Средствами машинной графики создается не только печатная продукция, но и рекламные ролики на телевидении, мультфильмы. Объясним, как кодируется изображение в памяти ...
0 комментариев