Навигация
Основні поняття теорії ймовірностей
РЕФЕРАТ
На тему:„Основні поняття теорії ймовірностей”
Виконав: Черненко Юрій
2007
Мета: Ознайомити учнів із поняттями випробування, випадкова подія, повна група подій, попарно несумісні події, рівноможливі події, елементарні події, вірогідна подія, неможлива подія; формувати поняття класичної ймовірності, умінь знаходити ймовірність подій за класичним означенням, розвивати інтерес до математики, використовувати історичний матеріал.
І. Організаційний момент
ІІ. Сприймання і усвідомлення понять: випробування, випадкова подія, вірогідна подія, неможлива подія
Теорія ймовірностей як самостійна наука виникла в середині ХVІІІ ст., коли були дуже поширені азартні ігри, тобто ігри, в яких результат залежить лише від випадку ( від французького слова hazard – „випадок”). До таких ігор належить гра в орлянку, ігри з кубиком, деякі карточні ігри тощо. У листування Б.Паскаля і П. Ферма з приводу задач, які постали в зв’язку з азартними іграми, було введено поняття ймовірності й математичного сподівання. Для розв’язування цих задач існуючий тоді апарат виявився недостатнім і було закладено основи нової науки.
Випадками нам здається те, що порушує звичайний хід подій. Ви поспішаєте на навчання, сідаєте в автобус, але автобус поламався, - і ви запізнилися на урок. Випадкова подія вплинула на ваш день, на звичайний розпорядок вашого життя.
Звичайно, не завжди випадкові події приносять негаразди. Наприклад ви зустріли на вулиці свого хорошого знайомого, не домовляючись. Або наприклад, поглядаєте таблицю виграшу лотарей і бачите номер вашого лотерейного квитка: тут випадкова подія – виграш – вам на користь.
Теорія ймовірностей – це галузь математики, що вивчає математичні моделі випадкових явищ. Наведемо приклад таких явищ. Якщо підкинути монету то вона може впасти або цифрою, або гербом догори; якщо слідкувати за певним атомом радіоактивної речовини, то за даний проміжок часу він може або розпастись, або не розпастись. Настання або не настання кожної з цих подій залежить від цілого ряду умов, які неможливо на перед врахувати, тому такі події вважають випадковими. Отже, випадкова подія – це подія яка може настати або не настати в результаті деякого експерименту, результат такого наперед не можна точно передбачити.
Уявіть собі, наприклад, урожай деякої сільськогосподарської культури на даній ділянці загинув через несподівану посуху. Це – важка випадковість. Є багато інших важких випадковостей, які поки що наука не може передбачити. Але наука прагне дати людині обґрунтовані методи боротьби з важкими випадковостями.
В тих випадках коли випадковість може принести користь, також бажано вивчати закони, за якими відбуваються випадкові явища, щоб зробити цю користь максимально великою.
Звичайно, щоб зробити висновок про ймовірність тієї або іншої випадкової події, необхідно провести не одне випробування чи експеримент.
Розглянемо деякий дослід, в результаті якого може з’явитись або не з’явитись подія А. Прикладом такого досліду можуть бути:
а) дослід – виготовлення певного виробу, подія А - стандартність цього виробу;
б) дослід – кидання монети, подія А – випав герб;
в) дослід – стрільба п’ятьма пострілами у мішень, подія А – вибито 30 очок;
г) дослід – введення програми у комп’ютер, подія А – безпомилковий ввід.
Загальним для усіх дослідів є те, що кожен із них може реалізуватися у певних умовах скільки завгодно разів. Такі досліди називають випробуваннями.
Випробування – це умови, в результаті яких відбувається чи не відбувається подія.
Виконання вправ
1. Відокремте події і випробування та запишіть результати у таблицю:
а) тягнемо карту з колоди поява пікового короля;
б) дістанемо лампу з коробки, вона бракована;
в) на екзамені витягнули білет № 17;
г) чуємо голос знайомого, навмання набравши голос знайомого;
Ґ) відкриваємо поштову скриньку і знаходимо лист;
д) стріляємо і влучаємо в ціль.
| Випробування | Подія | |
| а | ||
| б | ||
| в | ||
| г | ||
| Ґ | ||
| д |
Події бувають вірогідні (достовірні), випадкові та неможливі.
Випадковою подією називається подія, яка може відбутися, або не відбутися під час певного випробування.
Випадкові події позначають великими літерами, наприклад А,В,С,D,X,Y,A1,A2,…An.
Кожна випадкова подія є наслідком багатьох випадкових або невідомих нам причин, які впливають на подію. Тому неможливо завбачити наслідок одночинниго випробування.
Вірогідною ( достовірною) називають таку подію, яка за розглянутих умов обов’язково трапиться.
Неможливою називають таку подію, яка за розглянутих умов не може трапитись.
Наприклад, якщо в урні є лише білі кулі, то добування білої кулі з урн є достовірна подія, а добування з цієї урни кулі іншого кольору – неможлива подія.
Якщо кинути монету на площину, то поява герба буде випадковою подією, тому що замість герба може з’явитись надпис.
Виконання вправ
1. Наведіть приклади достовірних подій.
2. Наведіть приклади неможливих подій.
3. Які із подій є вірогідними ( завдання проектується через кодоскоп)?
А – два попадання при трьох пострілах;
В – навмання вибране трицифрове число не більше 1000;
С – випадання 12 очок при киданні двох гральних кубиків;
Д – випадання цифри три при киданні монети.
4.Які із подій є неможливими:
А – випадання 13 очок прикиданні двох гральних кубиків;
В – поява слова мама при випадковому наборі букв а,а,м,м,;
С – чотири попадання при трьох пострілах;
Д – поява на одній грані грального кубика число 8;
Похожие работы
... аксіоматичного визначення поняття ймовірності П.Л. Чебишев (1821–1894 р.) був творцем і ідейним керівником петербурзької математичної школи. Чебишев зіграв велику роль у розвитку багатьох розділів математики, у тому числі теорії ймовірностей. У своїй магістерській дисертації в першому розділі він уводить поняття ймовірності. Для цього він, насамперед, визначає рівно можливі події: «Якщо з ...
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... у рішенні. Точність як би здатна виникати нізвідки, і це міцно осідає в підсвідомості учнів. Приведу тільки один приклад з добротного у всіх інших відносинах "Керівництва до рішення задач по теорії ймовірностей і математичній статистиці" В. Е. Гмурмана. Імовірність появи події в кожнім з 100 незалежних іспитів постійна і дорівнює р=0,8. Знайти імовірність того, що подія з'явиться не менш 75 разів ...
... Метод моментів Метод моментів є одним із методів точечного оцінювання параметрів розподілу. Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів 1,2,…,k. Це означає, що відомий вид функції щільності fx(х, ), де = (1,2,…,k), якщо X безперервна (відомий вид функції ймовірності Р (X= х,), якщо X дискретна), але числові значення k параметрів не відомі. ...


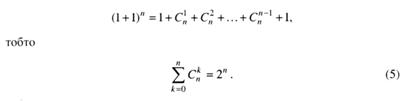


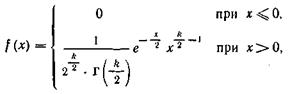
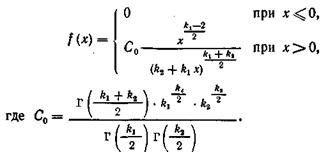

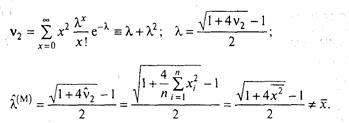
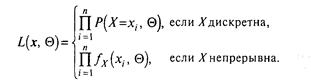
0 комментариев