Навигация
Проаналізуйте наведення нижче випробування і події та виділіть серед них вірогідні, неможливі та випадкові події
5. Проаналізуйте наведення нижче випробування і події та виділіть серед них вірогідні, неможливі та випадкові події.
| Випробування | Подія |
| Нагрівання дроту | Довжина дроту збільшилася |
| Підкидання гральної кості | Випало два очки |
| Огляд поштової скриньки | Знайдено три листи |
| Створено низьку температуру | Вода перетворилася на лід |
| Виконано постріл | Влучена в ціль |
| Тіло охолоджувалося | Його об’єм збільшився |
6. Вкажіть вірогідні, випадкові та неможливі події, які можуть відбутися при випробовуваннях, записаних у таблиці (через кодоскоп) :
| № п/п | Випробування | Випадкова подія | Вірогідна подія | Неможлива подія |
| 1 | Підкидання грального кубика | |||
| 2 | Підкидання монети | |||
| 3 | Витягування кулі із скриньки де є чорні та білі кулі | |||
| 4 | Витягування двох гральних карт | |||
| 5 | Заправка автомобіля бензином | |||
| 6 | Два постріли по мішені |
ІІІ. Сприймання і усвідомлення понять: повна група подій, попарно несумісні події, рівно можливі події, елементарні події
Означення 1. Випадкові події А1,А2...Ап утворюють повну групу подій, якщо внаслідок випробування хоча б одна з них з’явиться обов’язковою.
Приклад 1. Кидають шестигранний кубик. Позначимо події так:
А1 - випала грань 1;
А2 - випала грань 2;
А3 - випала грань 3;
А4 - випала грань 4;
А5 - випала грань 5;
А6 - випала грань 6.
Події А1,А2...А6 утворюють повну групу.
Виконання вправ
Чи утворюють повну групу такі групи подій:
а) випробування – кидання монети; події:
А1 – поява герба
А2 – поява цифри.
б) випробування – кидання двох монет; події:
А1 – поява двох гербів
А2 – поява двох цифр.
в) випробування – два постріли по мішені; події:
А1 – жодного попадання
А2 – одне попадання
А3 - два попадання.
Відповіді: а) так, б) ні, в) так
Означення 2. Події називаються несумісними, якщо поява однієї з них виключає появу інших подій в одному й тому ж випробуванні.
Приклад 2. Серед однорідних деталей у ящику є стандартні і не стандартні. Навмання беруть із ящика одну деталь.
Події:
А – взята стандартна деталь;
В – взята не стандартна деталь.
Несумісні тому, що взята лише одна деталь, яка не може бути водночас стандартною та нестандартною.
Виконання вправ
Чи є несумісними такі події:
а) випробування – кидання монети; події:
А1 – поява герба
А2 – поява цифри.
б) випробування – кидання двох монет; події:
В1 – поява герба на першій монеті
В2 – поява цифри на другій монеті.
в) випробування – витягування двох карт із колоди; події:
С1 – поява двох чорних карт
С2 – поява туза
С3 - поява дами
Відповіді: а) так, б) ні, в) ні
Означення 4. Події називаються рівно можливими, якщо немає причин стверджувати, що будь яка з них важливіша за інші.
Приклад 4. Події – поява 1,2,3,4,5 або6 очок при киданні шестигранного кубика – рівно можливі за умови, що центр його ваги не зміщений.
Виконання вправ
Чи є рівно можливими такі події:
а) випробування – кидання монети; події:
А1 – поява герба
А2 – поява цифри.
б) випробування – кидання неправильної ( зігнутої) монети; події:
В1 – поява герба
В2 – поява цифри.
в) випробування – постріл по мішені; події:
С1 – попадання
С2 – промах
г) випробування – кидання двох монет; події:
Д1 – поява двох гербів
Д2 – поява двох цифр
Д3 – поява одного герба і однієї цифри.
д) випробування – витягування однієї кари із колоди;події:
Е1 – поява карти червоної масті
Е2 – поява карти бубнової масті
Е3 – поява карти трефової масті
Е4 – поява карти пікової масті
є) випробування – грального кубика;події:
F1 – поява не менше трьох очок
F2 – поява не більше чотирьох очок.
Відповіді: а) так, б) ні, в) так г) ні, д) так, є) так
Тепер розглянемо важливе поняття простору елементарних наслідків.
Нехай виконується деякий експеримент, який має елементи випадковості. Кожне випробування може мати різні наслідки.
Наприклад, при киданні монети можуть бути два можливі наслідки: герб або напис.
При киданні монети може бути шість можливих наслідків.
У випробуванні постріл у мішень можна розглядати такі можливі наслідки, як влучення у мішень, або кількість вибитих очок, або координати точки влучення.
Отже, що приймати за наслідок випробування, залежить від умови задачі.
Означення 5. Елементарними наслідками називають такі події, які не можливо розділити на більш прості.
Множину усіх можливих елементарних наслідків називають простором елементарних наслідків.
Отже, якщо події:
1) утворюють повну групу подій
2) є несумісними;
3) є рівно можливими
то такі події утворюють простір елементарних подій або простір елементарних наслідків.
Виконання вправ
Чи утворюють простір елементарних наслідків такі події:
а) випробування – кидання монети; події:
А1 – поява герба
А2 – поява цифри.
б) випробування – кидання двох монет; події:
А1 – поява двох гербів
А2 – поява двох цифр.
в) випробування – кидання грального кубика; події:
С1 – поява не більше двох очок
С2 – поява трьох і чотирьох очок
С3 – поява не менше 5 очок;
г) випробування – постріл по мішені; події:
Д1 - попадання
Д2 – промах
д) випробування – два постріли по мішені; події:
Е0 – жодного попадання
Е1 – одне попадання
Е2 – два попадання
є) випробування – витягування двох карт із колоди;події:
F1 – поява двох червоних карт
F2 – поява двох чорних карт
Відповіді: а) так, б) ні, в) так г) так, д)ні, є) ні
IV Сприймання і усвідомлення класичного означення ймовірності
Якщо розглядати випадкову подію багато разів при однакових умовах, то можна виявити певну закономірність її появи або не появи. Таку закономірність називають ймовірною закономірність масових однорідних випадкових подій.
У теорії ймовірностей під масовими однорідними випадковими подіями розуміють такі події, які здійснюються багаторазово за однакових умов або багато однакових подій.
Наприклад, кинути одну монету 1000 разів або 1000 однакових монет кинути 1 раз у теорії ймовірностей вважають однаковими подіями.
Предметом теорії ймовірностей є вивчення ймовірнісних закономірностей масових однорідних випадкових подій.
Наприклад, коли в сім’ї повинна народитися дитина, ніхто не може передбачити хлопчик це буде чи дівчинка. Навіть, якщо, чекати, що в сім’ї буде декілька дітей (дві, три, чотири дитини), то і тут наперед не можна сказати скільки із них буде хлопчиків. Але в усіх країнах і серед усіх народів на 1000 народжених у середньому приходиться 511 хлопчиків і 489 дівчаток; ця вражаюча постійність народження дівчаток і хлопчиків відмічалась багатьма вченими, серед яких був і один із засновників теорії ймовірностей – французький математик Сімон Лаплас ( 1749-1827). Проглядаючи у свій час списки народжень по Парижу за 1745-1784 роки. Лаплас виявив, що відношення хлопчиків до загального числа народжень виявилося рівним приблизно 0,510, тобто менше 0,511. Не дивлячись на те, що різниця була дуже мала, Лаплас зробив висновок, що є якась причина, що збільшує число дівчаток, адже число народжень у Парижі за 39 років і в той час було уже досить великим; тому навіть таке мале відхилення н можна було пояснити звичайним випадком. І дійсно, Лаплас виявив причину відхилення: вона була в тому, що в число дітей, народжених у Парижі, входили також діти, підкинуті в спеціальний притулок – єдиний на всю Францію. Так як французькі селяни цінували в синах майбутніх робітників то вони частіше відкидали дівчаток, ніж хлопчиків. Відрахувавши підкинутих дітей, Лаплас отримав і для Парижа звичайне відношення числа хлопчиків до числа дівчаток.
Спробуємо тепер виявити дану закономірність через мову математики. Нехай маємо подію А, яка в кожному окремому випадку може відбутися або не відбутися. Нехай далі проведено N випробувань, із яких у М випадках подія А відбувалася, а в N-М випадках не відбулася. Частота події А ( тобто доля числа випробувань, при яких подія А мала місце) тут дорівнює М/N.
При цьому для великих N частота події виявляється приблизно постійною. Стійка частота окремої випадкової події називається ймовірною цієї події. Відношення числа подій, які сприяють події А, до загальної кількості подій простору, елементарних подій називається ймовірністю випадкової події і позначається Р (А).
Розглянемо випробування – кидання грального кубика;простір елементарних подій складається із подій:
А1 – поява числа 1;
А2 - поява числа 2;
А3 - поява числа 3;
А4 - поява числа 4;
А5 - поява числа 5;
А6 - поява числа 6.
Розглянемо подію А – випало парне число. Цій події А сприяють елементи події А2, А4, А6,.
Загальна кількість подій простору елементарних подій – 6.
Число подій, що сприяють події А – 3.
Ймовірність подій А:
Р(А)=3/6=1/2
Класичне означення ймовірності, запроваджене засновниками ймовірностей Б. Паска лем і П.Ферма, є: Р(А)=3/6=m/n
n- загальна кількість подій простору елементарних подій;
m- число подій, які сприяють події А.
Завдання.
Визначте ймовірність:
а) вірогідної події
б) неможливої події.
Відповідь: а) – 1, б) – 0.
Один французький рицар, кавалер де Маре, був пристрасним гравцем у кості. Він увесь час намагався розбагатіти за рахунок гри і для цього придумав різні складні правила, які, як йому здавалося, приведуть його до мети. В той час ( ХVІІ ст..) бажання розбагатіти за допомогою азартних ігор охопило, як хвороба, багатьох людей.
Де Маре придумав, зокрема, такі правила гри. Він пропонував кидати одну кость чотири рази підряд і бився об заклад що при цьому хоча б один раз випаде цифра 6; якщо ж цього не станеться – ні разу не випаде 6 очок, то виграє його противник. Де Маре вважав, що він буде частіше вигравати, ніж програвати, але все ж таки звернувся до свого знайомого, одного з найбільших математиків ХVІІ ст. – Блеза Паска ля ( 1623 – 1662) із проханням прорахувати, яка ймовірність виграшу в придуманій нім грі.
Попробуйте прорахувати й ви
При кожному окремому киданні ймовірність випадання 6 дорівнює 1/6. Ймовірність того, що не випаде 6 очок дорівнює 5/6.
Далі: кидаємо кості двічі. Повторимо дослід, що полягає в дворазовому киданні скажімо N раз. Тоді приблизно в 5/6 із цих N випадків на кость, кинутої перший раз, не випаде 6. Із числа цих 5/6 (6/6N)=(5/6)2 N випадків не випаде 6 і при другому киданні кості.
Таким чином, ймовірність того що при дворазовому киданні кості жодного разу не випаде 6 очок, дорівнює:
(5/6)2=26/36
точно так розраховується, що ймовірність того, що жодного разу не випаде 6 очок при триразовому киданні кості дорівнює:
(5/6)3=125/216.
Нарешті, ймовірність того, що при чотириразовому киданні жодного разу не випаде 6 , дорівнює:
(5/6)4=625/1296
Таким чином, для рицаря де Мере ймовірність програшу дорівнювала:
625/1294, тобто менше ½
тобто ймовірність виграшу була більша половини. Значить, при кожній грі більше половини шансів було за те, що лицар виграє. При багаторазовому повторі гри він майже напевне залишався у виграші.
Дійсно, чим більше лицар грав, тим більше він вигравав. Кавалер де Маре був дуже задоволений і вирішив, що відкрив правильний спосіб збагачення. Однак, поступово іншим гравцям стало зрозуміло, що ця гра для них не корисна і вони перестали грати з де Маре. Необхідно було придумати якісь інші правила і де Маре придумав нову гру. Але на цей раз лицар помилився. Чим більше він грав тим більше розорявся і залишився бідняком.
Найцікавіше в цьому історичному анекдоті те, що завдяки таким ось практичним запитам з’явилася теорія розрахунку випадкових явищ. У XVII і XVIII ст.. учені дивились на ці приклади, як на цікаві випадки застосування математичних знань до явищ, які не мають широкого розповсюдження. Адже, гравець у кості, який мріє про багатство, ніяк не заслуговує, щоб на допомогу йому була створена спеціальна наука.
Нині, ж основні поняття, методи, теореми та формули теорії ймовірностей ефективно використовують в техніці, економіці, у теоріях надійності та масового обслуговування, у плануванні та організації виробництва, у страховій та податковій справах, у соціології, у демографії та охороні здоров’я.
Похожие работы
... аксіоматичного визначення поняття ймовірності П.Л. Чебишев (1821–1894 р.) був творцем і ідейним керівником петербурзької математичної школи. Чебишев зіграв велику роль у розвитку багатьох розділів математики, у тому числі теорії ймовірностей. У своїй магістерській дисертації в першому розділі він уводить поняття ймовірності. Для цього він, насамперед, визначає рівно можливі події: «Якщо з ...
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
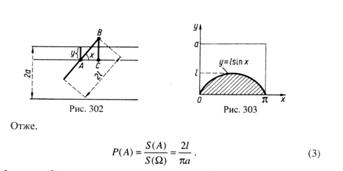
... у рішенні. Точність як би здатна виникати нізвідки, і це міцно осідає в підсвідомості учнів. Приведу тільки один приклад з добротного у всіх інших відносинах "Керівництва до рішення задач по теорії ймовірностей і математичній статистиці" В. Е. Гмурмана. Імовірність появи події в кожнім з 100 незалежних іспитів постійна і дорівнює р=0,8. Знайти імовірність того, що подія з'явиться не менш 75 разів ...
... Метод моментів Метод моментів є одним із методів точечного оцінювання параметрів розподілу. Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів 1,2,…,k. Це означає, що відомий вид функції щільності fx(х, ), де = (1,2,…,k), якщо X безперервна (відомий вид функції ймовірності Р (X= х,), якщо X дискретна), але числові значення k параметрів не відомі. ...


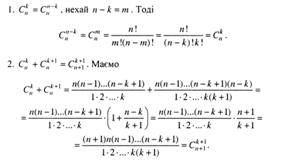
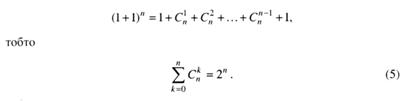


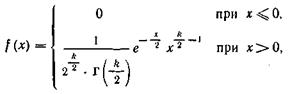
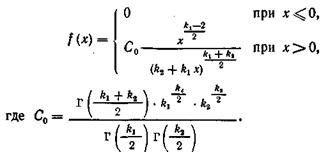

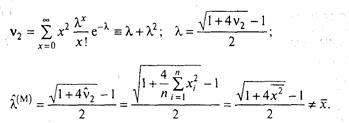
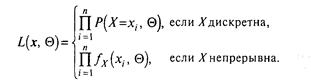
0 комментариев