Навигация
Системы линейных и дифференциальных уравнений
к/р № 1
1. Решить матричные уравнения и сделать проверку.
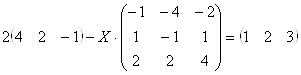
Решение:

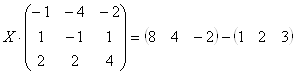

Найдём обратную матрицу 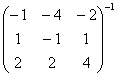 .
.
Обратной для матрицы А есть матрица ![]() , где
, где ![]() - определитель матрицы А, а элементы матрицы A* являются алгебраическими дополнениями соответствующих элементов матрицы А.
- определитель матрицы А, а элементы матрицы A* являются алгебраическими дополнениями соответствующих элементов матрицы А.
Тогда:
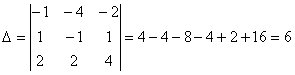 .
.
Найдем элементы матрицы А*:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда:
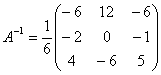 и для Х получим следующее выражение:
и для Х получим следующее выражение:

![]()
Выполним проверку:
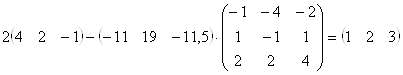
![]()
![]()
![]() - верное равенство.
- верное равенство.
Ответ: ![]() .
.
2. Даны координаты точек А, В, С. Найти уравнения сторон треугольника АВС. Найти уравнение одной из медиан треугольника АВС. Найти уравнение одной из высот треугольника АВС. Найти уравнение одной из биссектрис треугольника АВС. Найти площадь треугольника АВС.
| Вариант | А | В | С |
| 19 | (-3;1) | (-1;-3) | (1;3) |
Решение:
Уравнение прямой, проходящей через две точки можно записать как ![]() .
.
Тогда:
- уравнение стороны АВ: ![]()
- уравнение стороны АС: ![]()
- уравнение стороны ВС: ![]()
Найдем уравнение медианы ВМ, проведенной к стороне АС. Точка М – середина отрезка АС, следовательно координаты ![]() или
или ![]()
- уравнение медианы ВМ: ![]()
Найдём уравнение высоты АH, проведенной к стороне ВС. Уравнение стороны ВС ![]() с коэффициентом пропорциональности
с коэффициентом пропорциональности ![]() . Коэффициент пропорциональности перпендикулярной прямой будет
. Коэффициент пропорциональности перпендикулярной прямой будет ![]() и тогда уравнение высоты принимает вид
и тогда уравнение высоты принимает вид ![]() , где К – некая константа, значение которой найдем исходя из условия принадлежности точки А(-3; 1) уравнению высоты AH:
, где К – некая константа, значение которой найдем исходя из условия принадлежности точки А(-3; 1) уравнению высоты AH: ![]()
- уравнение высоты АН: ![]()
Будем искать уравнение биссектрисы угла С.
Прямые АС: ![]() и ВС:
и ВС: ![]() наклонены под острым углом к оси абсцисс (коэффициенты пропорциональности положительны), тогда угол между прямыми АС и ВС будет равен
наклонены под острым углом к оси абсцисс (коэффициенты пропорциональности положительны), тогда угол между прямыми АС и ВС будет равен ![]() , где
, где ![]() угол между прямыми ВС и АС и осью ОХ соответственно.
угол между прямыми ВС и АС и осью ОХ соответственно.
По формуле тангенса разности получаем, что
![]()
Половина угла С будет ![]()
Тангенс угла наклона биссектрисы к оси ОХ тогда составит:
![]()
Уравнение биссектрисы примет вид: ![]() , где К некая константа, значение которой определим из условия принадлежности точки С(1; 3) биссектрисе, т.е.
, где К некая константа, значение которой определим из условия принадлежности точки С(1; 3) биссектрисе, т.е.
![]()
Уравнение биссектрисы CL принимает вид ![]()
Для нахождения площади треугольника АВС воспользуемся формулой:
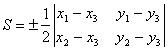 .
.
Тогда:
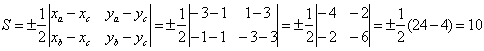 кв.ед.
кв.ед.
Выполним чертеж:
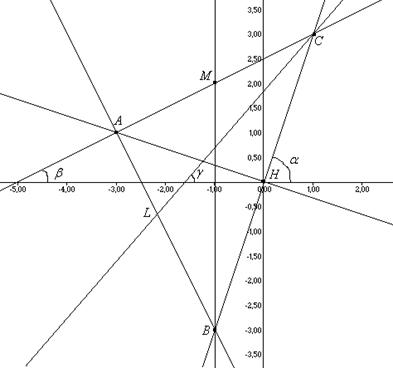
Ответ: АВ: ![]() АС:
АС: ![]() ВС:
ВС: ![]() - стороны треугольника
- стороны треугольника
ВМ: ![]() - медиана треугольника; АН:
- медиана треугольника; АН: ![]() - высота треугольника;
- высота треугольника;
СL: - биссектриса треугольника; S = 10 кв.ед.
3. Даны координаты точек А1 ,A2 ,А3 ,A4
Найти длину ребра А1А2. Составить уравнение ребра А1А4 и грани А1А2А3. Составить уравнение высоты опущенной из точки А4 на плоскость А1А2А3. Найти площадь треугольника А1A2A3 . Найти объем треугольной пирамиды А1A2А3A4
| N | Координаты точек | |||
| Вар | A1 | A2 | A3 | A4 |
| 2.19 | (8;6;4) | (10;5;5) | (5;6;8) | (8;10;7) |
Решение:
Воспользуемся формулой для вычисления расстояние между двумя точками:
![]()
Наши точки А1(8; 6; 4) и A2(10; 5; 5):
![]() ед.
ед.
Длина ребра А1А2 равна ![]() ед.
ед.
Составим уравнение прямой проходящей через точки А1(8; 6; 4) и A4(8; 10; 7).
Для этого воспользуемся уравнением: ![]()
![]() , т.е. А1А4:
, т.е. А1А4: ![]() .
.
Найдем уравнение плоскости, проходящей через точки А1(8; 6; 4), A2(10; 5; 5), А3(5; 6; 8).
Воспользуемся формулой: 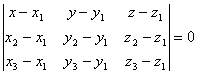
Подставим данные:
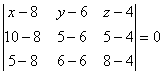 или
или 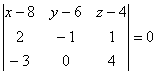
Т.е. уравнение грани А1А2А3:![]() или
или ![]()
Искомая высота проходит через точку A4(8; 10; 7) и перпендикулярна плоскости ![]() , имеющей вектор нормали
, имеющей вектор нормали ![]() .
.
Направляющий вектор высоты совпадает с вектором нормали плоскости, к которой проведена высота, следовательно, т.к. каноническое уравнение прямой ![]() , то
, то ![]() уравнение искомой высоты.
уравнение искомой высоты.
Площадь треугольника А1А2А3 можно найти по формуле: ![]() , где
, где ![]() - векторное произведение двух векторов
- векторное произведение двух векторов
![]() и
и ![]() .
.
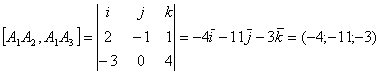
![]() кв.ед.
кв.ед.
Объем пирамиды можно найти по формуле: ![]() , где
, где ![]() - смешанное произведение трех векторов
- смешанное произведение трех векторов ![]() ,
, ![]() и
и ![]()
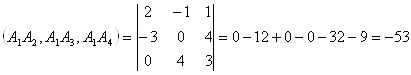
Тогда ![]() куб.ед.
куб.ед.
Ответ:
![]() ед.; А1А4:
ед.; А1А4: ![]() ; А1А2А3:
; А1А2А3:![]()
h: ![]() ;
; ![]() кв.ед.;
кв.ед.; ![]() куб.ед.
куб.ед.
Похожие работы
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
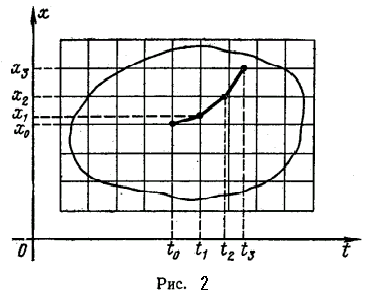
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... следует, что замена переменных z = Ф(t)y переводит систему уравнений (1) в систему уравнений с постоянными коэффициентами (см. примечание 3) 2. Неоднородная линейная система дифференциальных уравнений с периодическими коэффициентами. Рассмотрим система дифференциальных уравнений ż = F(t)z + g(t) (- ¥ < t < + ¥ ...
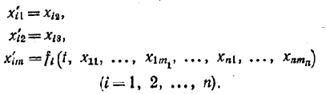

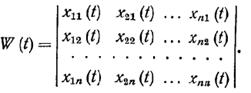
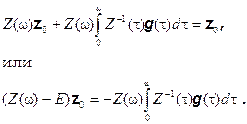
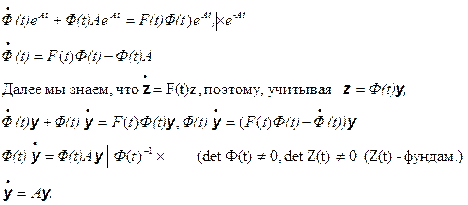
0 комментариев