Навигация
1. Найти следующие пределы.
а) ![]() б)
б) ![]()
Решение:
а) ![]() - неопределенность с бесконечностью. Раскроем скобки, приведем подобные и разделим числитель и знаменатель дроби на максимальную степень х. Получим:
- неопределенность с бесконечностью. Раскроем скобки, приведем подобные и разделим числитель и знаменатель дроби на максимальную степень х. Получим:
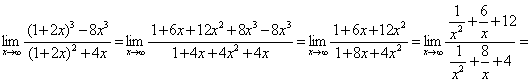
![]()
б) ![]() - неопределенность
- неопределенность ![]() . Избавимся от обнуляющего множителя, для этого числитель разложим на множители, а к знаменателю применим эквивалентную бесконечно малую: при
. Избавимся от обнуляющего множителя, для этого числитель разложим на множители, а к знаменателю применим эквивалентную бесконечно малую: при ![]()
![]() . Получим:
. Получим:
![]()
Ответ: а) 3; б) -2,5.
2. Найти производные функций, заданных в явном и неявном виде.
а) ![]() б)
б) ![]()
Решение:
а) Перепишем функцию![]() в виде экспоненты:
в виде экспоненты: ![]()

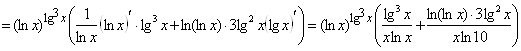
![]()
б) ![]() - продифференцируем обе части равенства по х.
- продифференцируем обе части равенства по х.
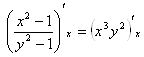
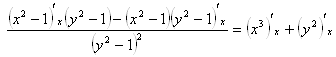


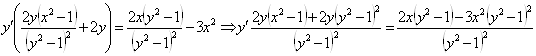
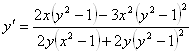
Ответ: решение выше.
3. Исследовать функцию методами дифференциального исчисления и построить ее график.
![]()
Решение:
1) Область определения функции: ![]() .
.
2) Четность, периодичность: ![]() , т.е. функция нечетная (симметричная относительно начала координат), не периодическая.
, т.е. функция нечетная (симметричная относительно начала координат), не периодическая.
3) Пересечение с осями:
с осью ОY: х = 0 – не принадлежит области определения.
с осью OX: y = 0 ![]() - решения нет, точек пересечения с осью ОХ нет.
- решения нет, точек пересечения с осью ОХ нет.
4) Асимптоты и поведение на бесконечности:
![]()
Наклонные асимптоты: y = kx + b, где ![]() b =
b = ![]()
![]()
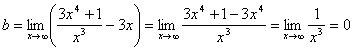
т.е. существует наклонная асимптота y = 3х.
5) Поведение возле точки разрыва:
Наша точка разрыва x = 0.
![]()
![]()
6) Критические точки:
Найдем производную функции y и решим уравнение y´ = 0.
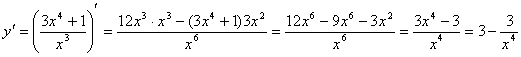
![]()
![]()

![]()
![]()
т.е. точка: (-1; -4) – точка максимума и (1; 4) - точка минимума.
7) Точки перегиба:
Найдем вторую производную функции y и решим уравнение y´´ = 0.
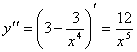 , значит
, значит ![]()
![]() - нет решений.
- нет решений.
При x > 0 функция выпуклая, при x < 0 вогнутая.
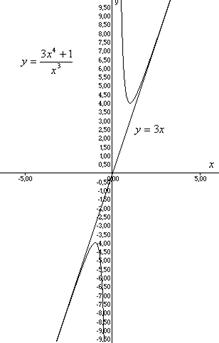
8) Построим график функции:
Похожие работы
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
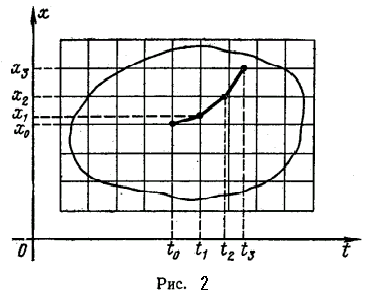
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... следует, что замена переменных z = Ф(t)y переводит систему уравнений (1) в систему уравнений с постоянными коэффициентами (см. примечание 3) 2. Неоднородная линейная система дифференциальных уравнений с периодическими коэффициентами. Рассмотрим система дифференциальных уравнений ż = F(t)z + g(t) (- ¥ < t < + ¥ ...
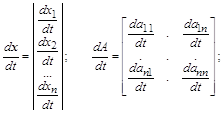
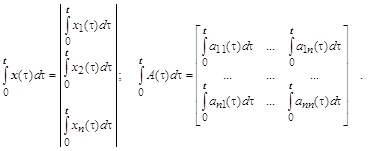
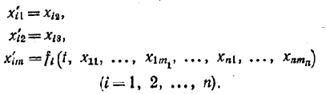

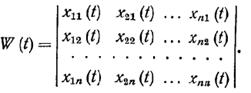
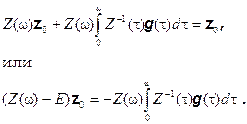
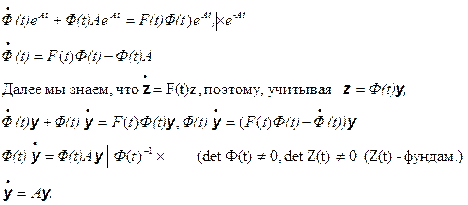
0 комментариев