Навигация
Найти собственные числа и собственные векторы матрицы А
4. Найти собственные числа и собственные векторы матрицы А.
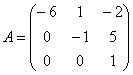 ;
;
Решение:
Найдем характеристическое уравнение матрицы А – определитель матрицы А -![]() Е, где Е – единичная матрица,
Е, где Е – единичная матрица, ![]() – независимая переменная.
– независимая переменная.
А –![]() Е =
Е = 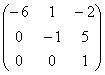 –
– ![]()
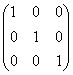 =
= 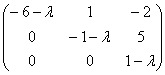 .
.
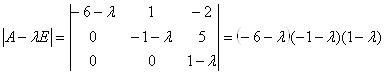
Найдем теперь собственные числа матрицы А – корни характеристического уравнения ![]() . Получаем:
. Получаем:
Получаем:
![]() ,
, ![]() ,
, ![]() .
.
Далее найдем собственные векторы матрицы А, соответствующие каждому из собственных чисел.
Пусть Х = ![]() – искомый собственный вектор.
– искомый собственный вектор.
Тогда система однородных уравнений (А -![]() Е) = 0 выглядит так:
Е) = 0 выглядит так:
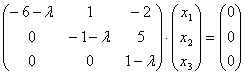 или
или 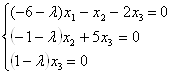
Эта однородная система линейных уравнений имеет множество решений, так как ее определитель равен нулю.
При ![]() система принимает вид:
система принимает вид:
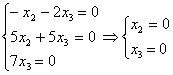
Общее решение этой системы 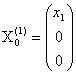 , где
, где ![]() любое число.
любое число.
В качестве собственного вектора достаточно взять любое частное решение.
Пусть, например, ![]() , тогда собственный вектор, соответствующий собственному числу
, тогда собственный вектор, соответствующий собственному числу ![]() , имеет вид:
, имеет вид: 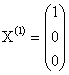 .
.
При ![]() система принимает вид:
система принимает вид:
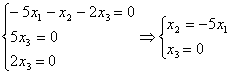
Общее решение этой системы 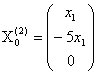 , где
, где ![]() любое число.
любое число.
Пусть, например, ![]() , тогда собственный вектор, соответствующий собственному числу
, тогда собственный вектор, соответствующий собственному числу ![]() , имеет вид:
, имеет вид: 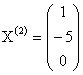 .
.
Аналогично при ![]() получаем систему
получаем систему
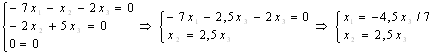
общее решение которой 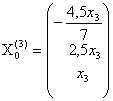 , где
, где ![]() любое число.
любое число.
Пусть ![]() , тогда собственный вектор, соответствующий собственному числу
, тогда собственный вектор, соответствующий собственному числу ![]() , имеет вид:
, имеет вид: 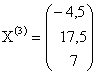 .
.
Ответ: ![]()
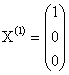 ,
, ![]()
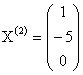 ,
, ![]()
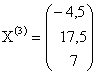 .
.
5. Решить систему методом Жорданa - Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.
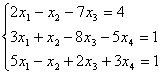
Решение:
Преобразуем расширенную матрицу системы к диагональному виду:
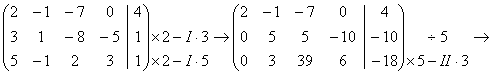
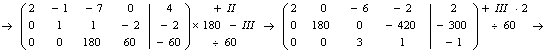

откуда получаем следующую систему
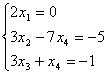 и
и
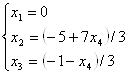 - общее решение исходной системы уравнений.
- общее решение исходной системы уравнений.
Частные решения получим присвоив конкретные значения переменной х4:
![]() тогда:
тогда: 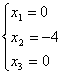 , т.е. решением будет вектор (0; -4; 0; -1)
, т.е. решением будет вектор (0; -4; 0; -1)
![]() тогда:
тогда: 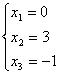 , т.е. решением будет вектор (0; 3; -1; 2).
, т.е. решением будет вектор (0; 3; -1; 2).
Выполним проверку общего решения:
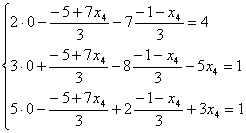
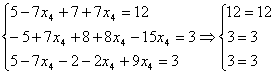 - верные равенства.
- верные равенства.
Ответ: 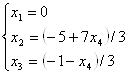 ; (0; -4; 0; -1); (0; 3; -1; 2).
; (0; -4; 0; -1); (0; 3; -1; 2).
к/р № 2
Похожие работы
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
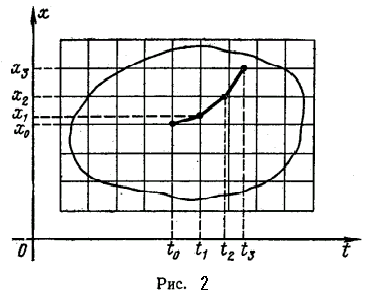
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
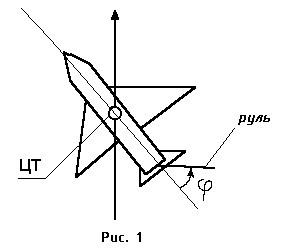
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... следует, что замена переменных z = Ф(t)y переводит систему уравнений (1) в систему уравнений с постоянными коэффициентами (см. примечание 3) 2. Неоднородная линейная система дифференциальных уравнений с периодическими коэффициентами. Рассмотрим система дифференциальных уравнений ż = F(t)z + g(t) (- ¥ < t < + ¥ ...
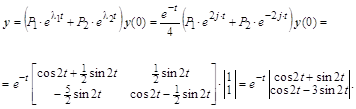
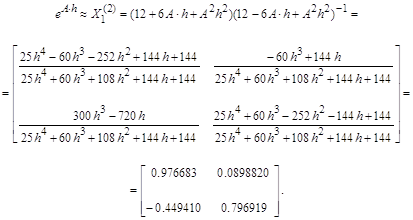
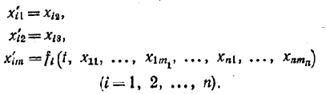

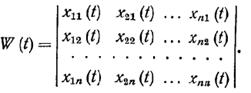
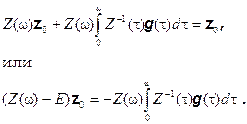
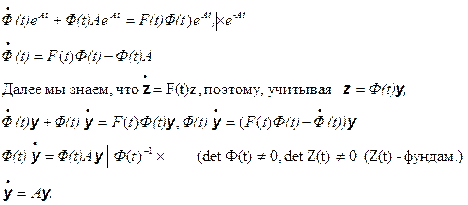
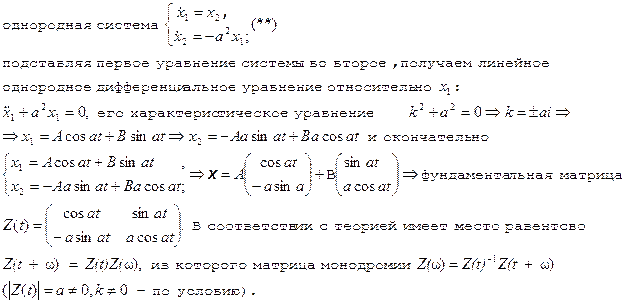
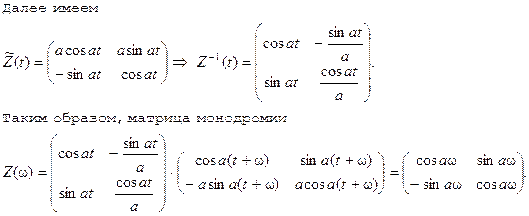
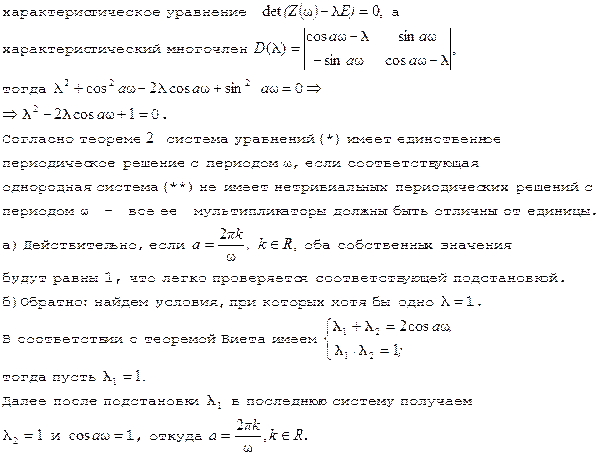
0 комментариев