Навигация
4. Найти
градиент функции Z в точке М.
уравнение матрица функция вектор дифференциальный
![]()
Решение:
Градиентом функции z в точке М является вектор grad (z) = ![]()
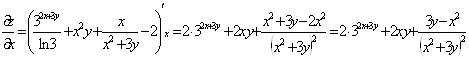
![]()
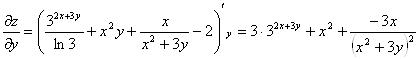
![]()
Т.е. grad(z) = ![]() .
.
Ответ: grad (z) = ![]() .
.
5. Вычислить неопределенные интегралы.
а) ![]() б)
б) ![]() с)
с) ![]() .
.
Решение:
а) ![]()
![]()
Рассмотрим интеграл ![]() :
:
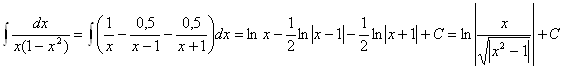
Тогда 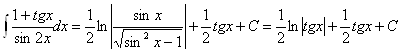
б) Воспользуемся формулой интегрирования по частям: ![]()
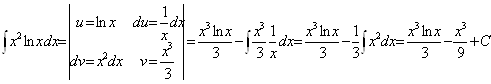
с) Разложим подинтегральное выражение на простые дроби:
![]()
![]() , т.е.
, т.е.
Тогда:
![]()
Ответ: решения выше.
6. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций вокруг оси OY
![]()
Решение:
Построим в координатной плоскости заданную фигуру.
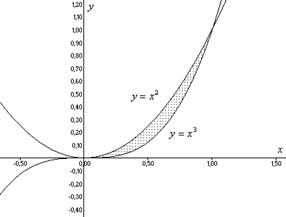
Объем тела, полученного вращением плоской фигуры около оси ОХ найдем по формуле:
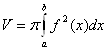
В нашем случае получаем:
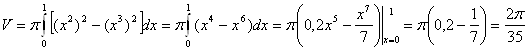 куб.ед.
куб.ед.
Ответ: ![]() куб.ед.
куб.ед.
7.
А) Найти общее решение дифференциального уравнения.
Б) Найти решение задачи Коши
В) Найти общее решение дифференциального уравнения.
а) ![]() ; б)
; б) ![]() ;
; ![]() ; в)
; в) ![]() .
.
Решение:
а) ![]() - уравнение с разделяющимися переменными.
- уравнение с разделяющимися переменными.
![]()
![]()
Возьмем интегралы:
![]()
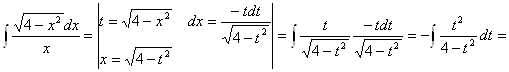
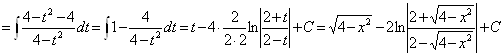
Таким образом
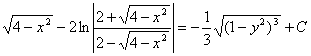 - общее решение уравнения, где С – произвольная константа.
- общее решение уравнения, где С – произвольная константа.
б) ![]() - уравнение Бернулли.
- уравнение Бернулли.
Решим его, выполнив замену ![]() . Тогда
. Тогда ![]() и исходное уравнение примет вид:
и исходное уравнение примет вид: 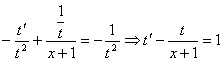 - линейное неоднородное уравнение первого порядка. Будем искать его решение в виде
- линейное неоднородное уравнение первого порядка. Будем искать его решение в виде ![]() , тогда
, тогда ![]() и
и
![]()
![]()
Функцию u будем искать такую, что ![]() , т.е.
, т.е.
![]()
Тогда: ![]()
В итоге ![]() и подставляя
и подставляя ![]() получаем
получаем ![]() - общее решение уравнения.
- общее решение уравнения.
Найдём решение задачи Коши для ![]() :
:
![]()
Искомое решение ![]() .
.
в) ![]() - неоднородное уравнение второго порядка с постоянными коэффициентами.
- неоднородное уравнение второго порядка с постоянными коэффициентами.
Его решение представляет собой сумму ![]() , где
, где ![]() - общее решение однородного уравнения,
- общее решение однородного уравнения, ![]() - частное решение неоднородного уравнения, зависящее от
- частное решение неоднородного уравнения, зависящее от ![]() и вида правой части неоднородного уравнения.
и вида правой части неоднородного уравнения.
Решением уравнения вида ![]() будет
будет ![]() , где
, где ![]() - корни характеристического уравнения
- корни характеристического уравнения ![]() .
.
Запишем характеристическое уравнение для ![]() :
:
![]() и найдем его корни:
и найдем его корни: ![]()
Тогда решение уравнения имеет вид: ![]() , где С1 и С2 – произвольные константы.
, где С1 и С2 – произвольные константы.
![]() будем искать в виде
будем искать в виде ![]()
Тогда:
![]()
![]() и подставляя в уравнение
и подставляя в уравнение ![]() получаем:
получаем:
![]()
откуда, приравнивая коэффициенты при соответствующих степенях х, получаем:
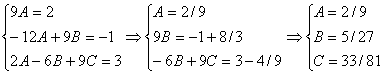 ,
,
т.е. ![]()
Общее решение неоднородного уравнения есть
![]()
Ответ: а) 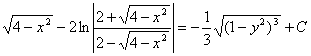 ;
;
б) ![]() ;
;
с) ![]() .
.
8.
а) Исследовать сходимость ряда.
б) Определить область сходимости ряда.
а) ![]() б)
б) ![]() .
.
Решение:
а) ![]() - рассмотрим ряд из абсолютных величин
- рассмотрим ряд из абсолютных величин ![]() .
.
Поскольку ![]() , то
, то ![]() .
.
Ряд ![]() сходится как обобщенный гармонический ряд степени р = 2 >1, следовательно и меньший ряд
сходится как обобщенный гармонический ряд степени р = 2 >1, следовательно и меньший ряд ![]() также сходится.
также сходится.
Исходный ряд ![]() сходится абсолютно.
сходится абсолютно.
б) Для степенного ряда вида ![]() интервалом сходимости будет интервал (x0 – R; x0 + R), где
интервалом сходимости будет интервал (x0 – R; x0 + R), где 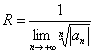 - радиус сходимости степенного ряда.
- радиус сходимости степенного ряда.
Для нашего ряда ![]() получим: x0 = 2 и общий член
получим: x0 = 2 и общий член ![]() .
.
Тогда: 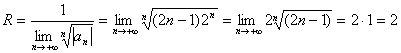
Получили интервал сходимости (2 – 2; 2 + 2) или (0; 4).
Рассмотрим концы интервала.
х = 4: ![]() - расходящийся гармонический ряд.
- расходящийся гармонический ряд.
х = 0: ![]() - условно сходящийся ряд Лейбница.
- условно сходящийся ряд Лейбница.
Ответ: а) сходится абсолютно; б) [0; 4).
Похожие работы
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
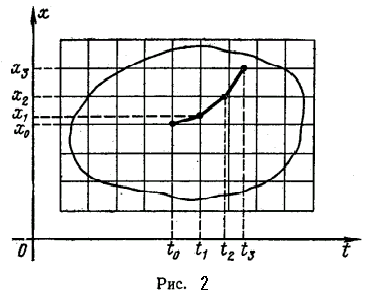
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... следует, что замена переменных z = Ф(t)y переводит систему уравнений (1) в систему уравнений с постоянными коэффициентами (см. примечание 3) 2. Неоднородная линейная система дифференциальных уравнений с периодическими коэффициентами. Рассмотрим система дифференциальных уравнений ż = F(t)z + g(t) (- ¥ < t < + ¥ ...
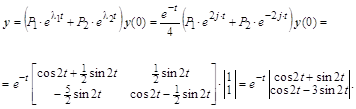
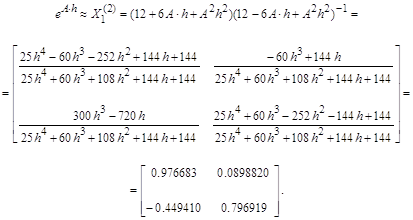
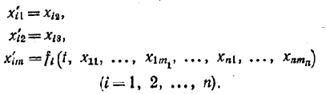

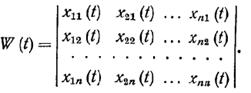
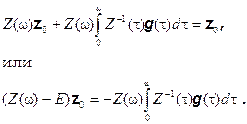
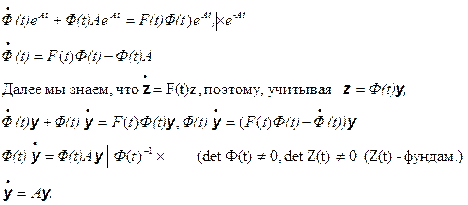
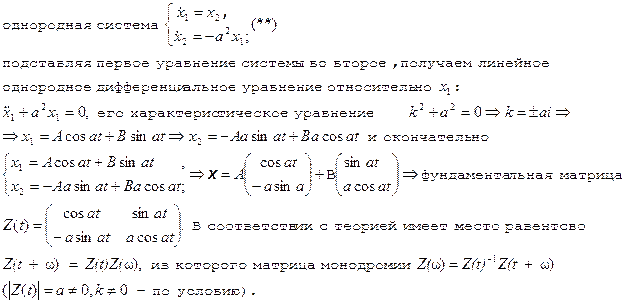
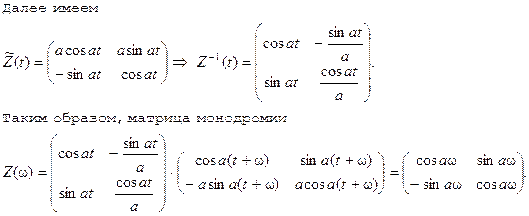
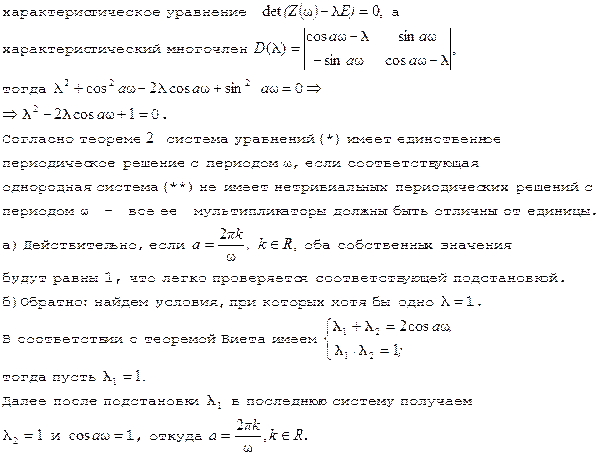
0 комментариев