Навигация
Вычисление средней арифметической по исходным данным о размерах инвестиций в основные фонды
4. Вычисление средней арифметической по исходным данным о размерах инвестиций в основные фонды
Для расчета применяется формула средней арифметической простой:
 ,
,
Причина расхождения средних величин, рассчитанных по исходным данным (0,61 млн. руб.) и по интервальному ряду распределения (0,62 млн. руб.), заключается в том, что в первом случае средняя определяется по фактическим значениям исследуемого признака для всех 25-ти предприятий, а во втором случае в качестве значений признака берутся середины интервалов ![]() и, следовательно, значение средней будет менее точным.
и, следовательно, значение средней будет менее точным.
Задание 2
По исходным данным (табл. 1) с использованием результатов выполнения Задания 1 необходимо выполнить следующее:
1. Установить наличие и характер корреляционной связи между признаками Инвестиции в основные фонды и Нераспределенная прибыль, образовав четыре группы с равными интервалами по каждому из признаков, используя методы:
а) аналитической группировки;
б) корреляционной таблицы.
2. Измерить тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое корреляционное отношение.
Сделать выводы по результатам выполнения задания 2.
Выполнение задания 2
Целью выполнения данного задания является выявление наличия корреляционной связи между факторным и результативным признаками, а также установление направления связи и оценка ее тесноты.
По условию Задания 2 факторным является признак Инвестиции в основные фонды, результативным – признак Нераспределенная прибыль.
1. Установление наличия и характера корреляционной связи между признаками Инвестиции в основные фонды и Нераспределенная прибыль методами аналитической группировки.
1. Применение метода аналитической группировки
Аналитическая группировка строится по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение ![]() результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения
результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения ![]() систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х- Инвестиции в основные фонды
Y – Нераспределенная прибыль
Групповые средние значения ![]() получаем из таблицы 3 (графа 3), основываясь на итоговых строках «Всего».
получаем из таблицы 3 (графа 3), основываясь на итоговых строках «Всего».
Вывод. Анализ данных табл. 7 показывает, что с увеличением размеров инвестиций в основные фонды от группы к группе систематически возрастает и нераспределенная прибыль по каждой группе предприятий, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками
2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации зІ и эмпирического корреляционного отношения з
Коэффициент детерминации зІ характеризует силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии ![]() признака Y в его общей дисперсии
признака Y в его общей дисперсии![]() :
:
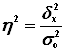
где уІ0 – общая дисперсия признака Y,
![]() – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y.
Общая дисперсия уІ0 характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных) и вычисляется по формуле
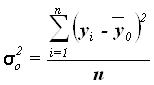 , (10)
, (10)
где yi – индивидуальные значения результативного признака;
![]() – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.
Межгрупповая дисперсия ![]() измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
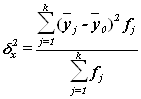 , (13)
, (13)
где ![]() – групповые средние,
– групповые средние,
![]() – общая средняя,
– общая средняя,
![]() –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число групп.
Для расчета показателей уІ0 и ![]() необходимо знать величину общей средней
необходимо знать величину общей средней ![]() , которая вычисляется как средняя арифметическая простая по всем единицам совокупности:
, которая вычисляется как средняя арифметическая простая по всем единицам совокупности:
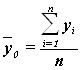
Значения числителя и знаменателя формулы имеются в табл. 7 (графы 3 и 4 итоговой строки). Используя эти данные, получаем общую среднюю ![]() :
:
![]() =
= ![]() =4,208 млн руб.
=4,208 млн руб.
Для расчета общей дисперсии ![]() применяется вспомогательная таблица 8.
применяется вспомогательная таблица 8.
Таблица 8. Вспомогательная таблица для расчета общей дисперсии
| Номер предприятия | Нераспределенная прибыль, млн. руб. |
|
|
| 1 | 2,7 | -1,508 | 2,2741 |
| 2 | 4,8 | 0,592 | 0,3505 |
| 3 | 6,0 | 1,792 | 3,2113 |
| 4 | 4,7 | 0,492 | 0,2421 |
| 5 | 4,4 | 0,192 | 0,0369 |
| 6 | 4,3 | 0,092 | 0,0085 |
| 7 | 5,0 | 0,792 | 0,6273 |
| 8 | 3,4 | -0,808 | 0,6529 |
| 9 | 2,3 | -1,908 | 3,6405 |
| 10 | 4,5 | 0,292 | 0,0853 |
| 11 | 4,7 | 0,492 | 0,2421 |
| 12 | 5,4 | 1,192 | 1,4209 |
| 13 | 5,8 | 1,592 | 2,5345 |
| 14 | 3,9 | -0,308 | 0,0949 |
| 15 | 4,2 | -0,008 | 0,0001 |
| 16 | 5,6 | 1,392 | 1,9377 |
| 17 | 4,5 | 0,292 | 0,0853 |
| 18 | 3,8 | -0,408 | 0,1665 |
| 19 | 2,0 | -2,208 | 4,8753 |
| 20 | 4,8 | 0,592 | 0,3505 |
| 21 | 5,2 | 0,992 | 0,9841 |
| 22 | 2,2 | -2,008 | 4,0321 |
| 23 | 3,6 | -0,608 | 0,3697 |
| 24 | 4,1 | -0,108 | 0,0117 |
| 25 | 3,3 | -0,908 | 0,8245 |
| Итого | 105,2 | 29,0593 |
Рассчитаем общую дисперсию:
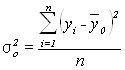 =
=![]()
Для расчета межгрупповой дисперсии ![]() строится вспомогательная таблица 9 При этом используются групповые средние значения
строится вспомогательная таблица 9 При этом используются групповые средние значения ![]() из табл. 7 (графа 5).
из табл. 7 (графа 5).
Рассчитаем межгрупповую дисперсию:

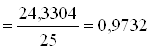
Определяем коэффициент детерминации:
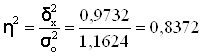 или 83,7%
или 83,7%
Вывод. 83,7% вариации нераспределенной прибыли предприятиями обусловлено вариацией инвестиции в основные фонды, а 16,3% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение з оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
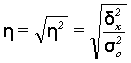
Рассчитаем показатель ![]() :
:
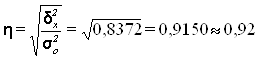
Вывод: согласно шкале Чэддока связь между размерами инвестиций в основные фонды и размерами нераспределенной прибыли предприятий является весьма тесной.
3. Оценка значимости (неслучайности) полученных характеристик связи признаков ![]() и
и ![]()
Показатели ![]() и
и ![]() рассчитаны для выборочной совокупности, т.е. на основе ограниченной информации об изучаемом явлении. Поскольку при формировании выборки на первичные данные могли иметь воздействии какие-либо случайные факторы, то есть основание полагать, что и полученные характеристики связи
рассчитаны для выборочной совокупности, т.е. на основе ограниченной информации об изучаемом явлении. Поскольку при формировании выборки на первичные данные могли иметь воздействии какие-либо случайные факторы, то есть основание полагать, что и полученные характеристики связи ![]() ,
, ![]() несут в себе элемент случайности. Ввиду этого, необходимо проверить, насколько заключение о тесноте связи, сделанное по выборке, будет правомерными и для генеральной совокупности, из которой была произведена выборка.
несут в себе элемент случайности. Ввиду этого, необходимо проверить, насколько заключение о тесноте связи, сделанное по выборке, будет правомерными и для генеральной совокупности, из которой была произведена выборка.
Проверка выборочных показателей на их неслучайность осуществляется в статистике с помощью тестов на статистическую значимость (существенность) показателя. Для проверки значимости коэффициента детерминации ![]() служит дисперсионный F-критерий Фишера, который рассчитывается по формуле
служит дисперсионный F-критерий Фишера, который рассчитывается по формуле  , где n – число единиц выборочной совокупности,
, где n – число единиц выборочной совокупности, ![]() m – количество групп,
m – количество групп,
![]() – межгрупповая дисперсия,
– межгрупповая дисперсия,
![]() – дисперсия j-ой группы (j=1,2,…, m),
– дисперсия j-ой группы (j=1,2,…, m),
![]() – средняя арифметическая групповых дисперсий.
– средняя арифметическая групповых дисперсий.
Величина ![]() рассчитывается, исходя из правила сложения дисперсий:
рассчитывается, исходя из правила сложения дисперсий:
![]() , где
, где ![]() – общая дисперсия.
– общая дисперсия.
Для проверки значимости показателя ![]() рассчитанное значение F-критерия Fрасч сравнивается с табличным Fтабл для принятого уровня значимости
рассчитанное значение F-критерия Fрасч сравнивается с табличным Fтабл для принятого уровня значимости ![]() и параметров k1, k2, зависящих от величин n и m: k1=m-1, k2=n-m. Величина Fтабл для значений
и параметров k1, k2, зависящих от величин n и m: k1=m-1, k2=n-m. Величина Fтабл для значений ![]() , k1, k2определяется по таблице распределения Фишера, где приведены критические (предельно допустимые) величины F-критерия для различных комбинаций значений
, k1, k2определяется по таблице распределения Фишера, где приведены критические (предельно допустимые) величины F-критерия для различных комбинаций значений ![]() , k1, k2. Уровень значимости
, k1, k2. Уровень значимости ![]() в социально-экономических исследованиях обычно принимается равным 0,05 (что соответствует доверительной вероятности Р=0,95).
в социально-экономических исследованиях обычно принимается равным 0,05 (что соответствует доверительной вероятности Р=0,95).
Если Fрасч>Fтабл, коэффициент детерминации ![]() признается статистически значимым, т.е. практически невероятно, что найденная оценка
признается статистически значимым, т.е. практически невероятно, что найденная оценка ![]() обусловлена только стечением случайных обстоятельств. В силу этого, выводы о тесноте связи изучаемых признаков, сделанные на основе выборки, можно распространить на всю генеральную совокупность.
обусловлена только стечением случайных обстоятельств. В силу этого, выводы о тесноте связи изучаемых признаков, сделанные на основе выборки, можно распространить на всю генеральную совокупность.
Если Fрасч<Fтабл, то показатель ![]() считается статистически незначимым и, следовательно, полученные оценки силы связи признаков относятся только к выборке, их нельзя распространить на генеральную совокупность.
считается статистически незначимым и, следовательно, полученные оценки силы связи признаков относятся только к выборке, их нельзя распространить на генеральную совокупность.
Фрагмент таблицы Фишера критических величин F-критерия для значений ![]() =0,05; k1=3,4,5; k2=21–32 представлен ниже:
=0,05; k1=3,4,5; k2=21–32 представлен ниже:
| k2 | ||||||||||||
| k1 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| 3 | 3,07 | 3,05 | 3,03 | 3,01 | 2,99 | 2,98 | 2,96 | 2,95 | 2,93 | 2,92 | 2,91 | 2,90 |
| 4 | 2,84 | 2,82 | 2,80 | 2,78 | 2,76 | 2,74 | 2,73 | 2,71 | 2,70 | 2,69 | 2,68 | 2,67 |
| 5 | 2,68 | 2,66 | 2,64 | 2,62 | 2,60 | 2,59 | 2,57 | 2,56 | 2,54 | 2,53 | 2,52 | 2,51 |
Расчет дисперсионного F-критерия Фишера для оценки ![]() =83,7%, полученной при
=83,7%, полученной при ![]() =1,1624,
=1,1624, ![]() =0,9732:
=0,9732:
Fрасч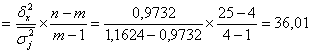
Табличное значение F-критерия при ![]() = 0,05:
= 0,05:
| n | m | k1=m-1 | k2=n-m | Fтабл( |
| 25 | 4 | 3 | 21 | 3,07 |
ВЫВОД: поскольку Fрасч>Fтабл, то величина коэффициента детерминации ![]() =83,7% признается значимой (неслучайной) с уровнем надежности 95% и, следовательно, найденные характеристики связи между признаками Инвестиции в основные фонды и Нераспределенная прибыль правомерны не только для выборки, но и для всей генеральной совокупности фирм.
=83,7% признается значимой (неслучайной) с уровнем надежности 95% и, следовательно, найденные характеристики связи между признаками Инвестиции в основные фонды и Нераспределенная прибыль правомерны не только для выборки, но и для всей генеральной совокупности фирм.
Задание 3
По результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить:
1) ошибку выборки среднего размера инвестиций и границы, в которых будет находиться средний размер инвестиций в генеральной совокупности.
2) ошибку выборки доли предприятий с инвестициями в основные фонды 0,76 млн. руб. и более и границы, в которых будет находиться генеральная доля.
Выполнение Задания 3
Целью выполнения данного Задания является определение для генеральной совокупности предприятий региона границ, в которых будут находиться средний размер инвестиций, и доля предприятий с инвестициями в основной фонд не менее 0,76 млн. руб.
Похожие работы
... если перенести начало отсчета в середину рассматриваемого периода. Прогнозирование и интерполяция Прогнозирование (экстраполяция) – это определение будущих размеров экономического явления. Интерполяция – это определение недостающих показателей уровней ряда. Наиболее простым методом прогнозирования является расчет средних характеристик роста (средний абсолютный прирост, средний темп роста и т.д.) ...
... сдвигов: (3) деление индекса переменного состава на индекс структурных сдвигов дает индекс цен постоянного состава, или обычный агрегатный индекс цен: (4) При статистическом изучении цен часто качественно разнородные по своему потребительскому назначению товары объединяются в совокупность, обладающая новыми качествами, в таких случаях средняя цена теряет свое реальное значение, и ...
... что и доходы, и расходы населения с каждым годом растут, разница между доходами и расходами снижается. Это далеко не положительно влияет на благосостояние населения России. Во-вторых, экономико-статистический анализ уровня жизни населения России имеет несколько отраслей, важнейшей из которых является статистика домашних хозяйств населения. Показатели, изучаемые в данной отрасли, используются в ...
... технологических цепочек; применения общестатистических методов (корреляции, индексного, табличного, графического и др.) к новому объекту исследования — ФПГ. 2. Методика статистического анализа функционирования финансово-промышленной группы и ее технологических цепочек, включающая, разработанные на основе аддитивных, мультипликативных и смешанных моделей, алгоритмы статистического анализа ...

0 комментариев