Елементи сферичної геометрії

2.1 Елементи сферичної геометрії

У цьому пункті розглянуті елементи так званої сферичної геометрії - геометрії сфери Евклідова простору. Найкоротшими (геодезичними) або прямими лініями на сфері є більші окружності, тобто такі окружності, площини яких проходять через центр даної сфери.

Тому що будь-які два більших кола перетинаються, то в сферичній геометрії не здійснюється ні постулат Евкліда, ні аксіома паралельності Лобачевского. У цій геометрії не виконується також ряд інших фактів абсолютної геометрії.

Наприклад, прямі в сферичній геометрії замкнуті й на них неможливо встановити поняття крапки, що лежить «між» для трьох крапок, тому що кожну із цих крапок на окружності можна вважати крапкою, що лежить між двома іншими. Дві крапки на великому колі визначають два відрізки й прямі мають кінцеву довжину. Таким чином, аксіоми порядку в сферичній геометрії повинні описувати властивості циклічного розташування крапок на прямій. І все-таки, незважаючи на зазначені розходження в сферичній геометрії є багато властивостей, аналогічних відповідним властивостям в евклідовій геометрії й геометрії Лобачевского. Ці геометрії, включаючи й геометрію досить малих шматків сфери, в основних питаннях не протиставляються між собою, а копіюють один одного.

Візьмемо на сфері три крапки А, В, З, що не лежать в одній площині із центром Про дану сферу. Сукупність цих крапок і дуг АВ, ВР і АС більших окружностей, менших півоберту, називається сферичним трикутником АВС. Крапки А, В, С називаються вершинами сферичного трикутника, а дуги, АВ, ВР, АС — його сторонами. Кутом А сферичним трикутником АВС називається, кут між дотичними, проведеними до дуг АВ і АС у крапці їхнього перетинання А. Очевидно, цей кут є лінійним кутом двогранного кута, утвореного площинами більших окружностей АВ і АС. Ясно, що сферичний трикутник можна одержати за допомогою тригранного кута, якщо перетнути його сферою, центр якої буде збігатися з вершиною даного кута. Справді, у перетинанні сфери із гранями даного тригранного кута одержимо сферичний трикутник.

Зі шкільного курсу геометрії відомо, що в тригранному куті будь-який його плоский кут менше суми двох інших плоских кутів і більше їхньої різниці. У геометрії сфери цій пропозиції відповідає наступна теорема. У всякому сферичному трикутнику кожна сторона менше суми двох інших його сторін і більше їхньої різниці.

На підставі цієї теореми, як і у звичайній планіметрії, доводиться, що в сферичному трикутнику проти більшої сторони лежить більший кут і, обернено, проти більшого кута лежить більша сторона.

У цій геометрії є сферичні двукутники - фігури більше прості, чим сферичні трикутники. Сферичний двукутник по визначенню, представляє частину сфери, обмежену двома більшими півколами, що перетинаються у двох діаметрально протилежних крапках.

Симетрія сфери щодо діаметральної площини й поворот її навколо діаметра на даний кут, мабуть, являють собою приклади перетворень сфери, при яких відстані між будь-якими двома крапками дорівнює відстані між їхніми образами. Приведемо загальне визначення.

Перетворення сфери, при яких зберігаються відстані між будь-якими двома її крапками, називаються рухами. Сферична геометрія вивчає властивості фігур, що зберігаються при будь-яких рухах сфери.

Полярні трикутники

Усяка площина , що проходить через центр сфери, перетинає цю сферу по великій окружності. Кінці А, А' діаметра, перпендикулярного площини , називаються полюсами цієї окружності. У цьому випадку більша окружність називається полярою крапок А и А'.

Очевидно, всі крапки поляри вилучені від свого полюса на відстань, рівне R/2, де R позначає радіус даної сфери. Ясно також, що якщо дана крапка вилучена від двох крапок великої окружності на відстань R/2, то вона є полюсом цієї великої окружності. Перейдемо тепер до визначення полярного трикутника.

Якщо вершини трикутника АВС є полюсами сторін іншого сферичного трикутника А₁У₁С₁, то цей останній називається полярним трикутником стосовно даного.

Таким чином, радіус-вектор  перпендикулярний векторам  і , тобто

Аналогічно будемо мати

Звідси треба, що якщо трикутник А₁У₁С₁ буде полярним до трикутника АВС, то трикутник АВС у свою чергу буде полярним стосовно трикутника А₁У₁С₁.

Таким чином, сферичні трикутники АВС і А₁У₁С₁, взаємно полярні один одному.

Будемо позначати вершини й кути сферичного трикутника більшими буквами латинського алфавіту А, В, С, а протилежні їм сторони — відповідними малими буквами того ж алфавіту а, Ь, с. Вершини й протилежні їм сторони полярного трикутника будемо позначати тими ж буквами з індексами А₁, В₁, С₁, відповідно a₁, b₁, c₁.

Лінійні елементи трикутника тут і в подальших формулах входять у вигляді відносин до радіуса сфери, тому доцільно ввести наступне поняття наведеної довжини. Відстань між двома крапками на сфері, віднесене до її радіуса, будемо називати наведеною відстанню.

Доведемо наступну пропозицію про взаємно полярні трикутники.

Теорема. Кут одного сферичного трикутника й відповідна йому наведена сторона взаємно полярного трикутника доповнюють один одного до , тобто

і т.д. Тому що

 (*)

Те з (*) треба, що

Таким чином, виводимо

Аналогічно доводяться інші рівності:

Перейдемо до висновку деяких формул сферичної геометрії.

Формули прямокутного трикутника в сферичній геометрії

Перейдемо до висновку деяких формул сферичної геометрії. Нехай в евклідовому просторі нам дана сфера радіуса R. Візьмемо на ній прямокутний трикутник AВС зі сторонами a, b, з, які будуть дугами більших кіл відповідно ВР, СА й АВ, причому вмовимося вважати (мал. 2). Останнє означає, що дотичні в крапці З, проведені до більших дуг СА, СВ, перпендикулярні. З'ясуємо зв'язок між лінійними й кутовими елементами даного прямокутного трикутника.

Опустимо із крапки В перпендикуляри ВР₁, і ВА₁ на прямі ОС і ОА Евклідова простору. Із трикутника ОВС₁, маємо

 (*)

Аналогічно із трикутників OBA₁і BA₁C₁ треба, що

 (**)

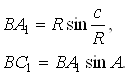Крім із цих трьох співвідношень BC₁ і BA₁, одержимо

 (1.1)

Формула (1.1) показує, що синус наведеного катета рівняється синусу наведеної гіпотенузи, помноженому на синус протилежного кута трикутника.

У попереднім міркуванні підстава С₁, перпендикуляра ВР₁, може збігатися із центром сфери або бути лівіше його на діаметрі ОС. Але можна переконатися, що одержувані нижче формули, як і формула (1.1), будуть завжди справедливі. До речі відзначу ще раз, що розглядаються тільки такі сферичні трикутники, які визначаються його вершинами й найменшими дугами більших окружностей, попарно їх з'єднуючими.

З'ясуємо зв'язок гіпотенузи c з катетами а й b. Із трикутника ОВС₁, маємо

 (1.2)

Далі із трикутника ОВА₁ і ОС₁А₁ треба, що

Крім із отриманих трьох рівностей ОС₁ і ОА₁ будемо мати

. (1.3)

Ця формула виражає теорему Піфагора: косинус наведеної гіпотенузи прямокутного трикутника рівняється добутку косинусів наведених катетів. Аналогічним образом виводяться інші формули. Наприклад, із прямокутного трикутника А₁ВР₁ треба, що

 (1.4)

Далі, тому що

те з (1.2) маємо

 (1.5)

З іншого боку,

 (1.6)

З (*, 1.4- 1.6) випливає, що

 (1.7)

Поряд із цією формулою справедлива також парна формула

 (1.7')

Перемножуючи останні два співвідношення, одержимо

Відкидаючи ненульові співмножники й застосовуючи теорему Піфагора, остаточно будемо мати

 (1.8)

Візьмемо тепер інше вираження А₁С₁ через соs A. Тому що

те з (**) і (1.5-1.6), маємо

Звідси треба, що

 (1.9)

З (1.1) випливає також, що

Останні дві рівності дають

Або

 (1.10)

Доведені формули прямокутного трикутника можна виписати, користуючись так званим правилом Непера. Щоб сформулювати це правило, умовимося розташовувати елемент прямокутного трикутника а, В, з, А, b у зазначеному на циклічному порядку.

Для кожного із цих елементів попередній і наступний елементи називаються прилеглими, а інші два елементи — протилежними. Для катета b, наприклад, елементи a, А будуть прилеглими, а елементи з, В — протилежними. Прилеглими елементами для гіпотенузи є кути A і В, а протилежними — катети а й b.

Сформулюємо тепер правило Непера. Косинус будь-якого елемента сферичного прямокутного трикутника рівняється добутку синусів протилежних елементів або добутку котангенсів прилеглих елементів. Якщо під знаком функції коштує катет, то тригонометрична функція міняється на суміжну - синус а косинус, тангенс на котангенс і навпаки. Помітимо також, що у всіх формулах довжини катетів і гіпотенузи діляться на радіус сфери R.

Формули косокутного трикутника в сферичній геометрії

Одержимо сНачало теорему косинусів. Нехай АВС довільний сферичний трикутник. Опустимо з вершини У висоту ВD. Застосовуючи до трикутника ВDС теорему Пифагора, одержимо

,

де d=AD, a=BC, b=BC, AB=c.

Перепишемо попередню рівність, другий множник формули косинуса різниці:

.(1.11)

Перший і третій множники в першому члені правої частини по теоремі Піфагора дають . Спростимо другий член у правій частині. Тому що

,

те заміняючи  по формулі (1.9) на , одержимо

Таким чином, з (1.11) треба, що

 (1.12)

Ця залежність, що виражає сторону сферичного трикутника через дві інші сторони в косинус протилежного кута, називається теоремою косинусів.

Доведемо тепер теорему синусів. Із прямокутного трикутника АВ і ВDС (мал. 6) одержуємо

Звідси треба, що

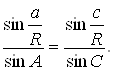
Якщо опустити тепер висоту з вершини А, то будемо мати

Отже

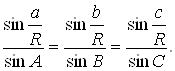 (1.13)

Ці залежності сторін і синусів протилежних кутів становлять теорему синусів сферичного трикутника АВС.

Друга теорема косинусів

Припустимо, що сферичний трикутник А₁У₁С₁, є полярним до даного трикутника АВС. Застосовуючи до нього теорему косинусів, одержимо

Але в силу формул (див. Полярні трикутники), маємо

Заміняючи в попередній рівності сторони й кути тільки що виписаними вираженнями, одержимо

Або

 (*)

Формула й становить зміст 2-й теореми косинусів: Косинус кута сферичного трикутника дорівнює добутку косинусів двох інших кутів, узятому зі зворотним знаком, і складеному з добутком синусів тих же кутів на косинус наведеної протилежної сторони. Аналогічні дві формули можна одержати круговою заміною лінійних і кутових елементів даного трикутника АВС.

Із другої теореми косинусів треба, що в сферичній геометрії не існує нерівних трикутників з відповідно рівними кутами. Інакше кажучи, якщо кути, одного сферичного трикутника дорівнюють відповідним кутам іншого сферичного трикутника, те такі трикутники рівні.

На закінчення встановимо лише збіг формул сферичної геометрії для фігур з малими лінійними розмірами з відповідними формулами евклідової геометрії.

Про сферичну геометрію в малому

Нехай лінійні розміри а, b, зі сферичного трикутника малі в порівнянні з радіусом сфери R. Очевидно, ці умови можна здійснити за рахунок малості зазначених лінійних розмірів або за рахунок вибору досить великого значення R. З формули, що виражає теорему косинусів, треба

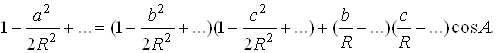
З огляду на в цій рівності члени до другого порядку малості включно, одержимо теорему косинусів евклідової геометрії:

 (1.14)

У випадку прямокутного сферичного трикутника з кутом маємо cos A=0 і формула (1.12) у межі приводить до співвідношення

,

тридцятимільйонну теорему Піфагора в геометрії Евкліда. Це рівність треба також з (1.14) при .

Тому що при малих розмірах наведених сторін їхні синуси в першому наближенні пропорційні аргументам, то з (1.13) випливають два зв'язки

,

теорему синусів в евклідовій геометрії.

Отже, формули сферичної геометрії для фігур з малими лінійними розмірами в порівнянні з радіусом сфери збігаються з відповідними формулами евклідової геометрії. Аналогічний результат одержимо нижче при розгляді формул геометрії Лобачевского.