Навигация
Знайдемо найбільше ціле значення параметра а, при якому рівняння cos2x + asinx = 2a – 7 має рішення
3. Знайдемо найбільше ціле значення параметра а, при якому рівняння cos2x + asinx = 2a – 7 має рішення.
Рішення: перетворимо задане рівняння:
cos2x + asinx = 2a – 7; 1 – 2sin2х – asinx = 2a – 7; sin2х - ![]() asinx + a – 4 = 0;
asinx + a – 4 = 0;
(sinх – 2) · ![]() = 0.
= 0.
Рішення рівняння (sinх – 2) · ![]() = 0 дає:
= 0 дає:
(sinх - 2) = 0; х належить порожній множині.
sinх - ![]() = 0; х = (-1)n arcsin
= 0; х = (-1)n arcsin ![]() + πn, n
+ πn, n ![]() Z при
Z при ![]() ≤ 1. Нерівність
≤ 1. Нерівність ![]() ≤ 1 має рішення 2 ≤ а ≤ 6, звідки треба, що найбільше ціле значення параметра а дорівнює 6.
≤ 1 має рішення 2 ≤ а ≤ 6, звідки треба, що найбільше ціле значення параметра а дорівнює 6.
Відповідь: 6.
4. Указати найбільше ціле значення параметра а, при якому корінь рівняння 4х2 - 2х + а = 0 належить інтервалу (- 1; 1).
Рішення: корінь заданого рівняння рівні: х1 =![]() (1+
(1+ ![]() )
)
х2 =![]() , при цьому а ≤
, при цьому а ≤ ![]() .
.
За умовою -1 < ![]() (1+
(1+ ![]() ) < 1
) < 1 ![]() <
< ![]() < 3,
< 3,
- 1 < ![]() < 1
< 1 ![]() >
> ![]() > - 3.
> - 3.
Рішенням, що задовольняють зазначеним подвійним нерівностям, буде рішення подвійної нерівності: - 3 < ![]() < 3.
< 3.
Нерівність - 3 < ![]() виконується при всіх а ≤
виконується при всіх а ≤ ![]() , нерівність
, нерівність ![]() < 3 – при - 2 < а ≤
< 3 – при - 2 < а ≤ ![]() . Таким чином, припустимі значення параметра а лежать в інтервалі (-2;
. Таким чином, припустимі значення параметра а лежать в інтервалі (-2; ![]() .
.
Найбільше ціле значення параметра а із цього інтервалу, що одночасно належить і інтервалу (-1; 1), дорівнює 0.
Відповідь: 0.
5. При яких значеннях параметра а число корінь рівняння
![]() 2 -
2 -![]() х
х ![]() = 0 дорівнює а?
= 0 дорівнює а?
Рішення: побудуємо ескіз графіка функції, в = ![]() 2 -
2 -![]() х
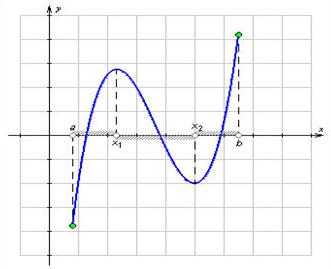
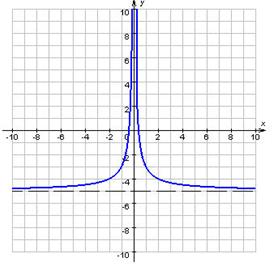
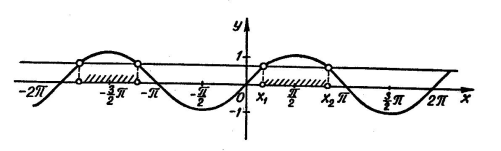
х ![]() при цьому врахуємо, що функція в – парна і її графік – симетричний щодо осі ординат, у силу чого можна обмежитися побудовою тільки його правої частини ( х ≥ 0). Також урахуємо, що тричлен х2 - 8х + 7 має коріння х = 1 і х = 7, при х = 0 в = 7, а при х = 4 – мінімум, рівний – 9. На малюнку: пунктирними прямими зображена парабола
при цьому врахуємо, що функція в – парна і її графік – симетричний щодо осі ординат, у силу чого можна обмежитися побудовою тільки його правої частини ( х ≥ 0). Також урахуємо, що тричлен х2 - 8х + 7 має коріння х = 1 і х = 7, при х = 0 в = 7, а при х = 4 – мінімум, рівний – 9. На малюнку: пунктирними прямими зображена парабола
в = х2 - 8х + 7 з мінімумом умін рівним - 9 при х хв = 4, і коріннями х1 = 1 і х2 = 7;
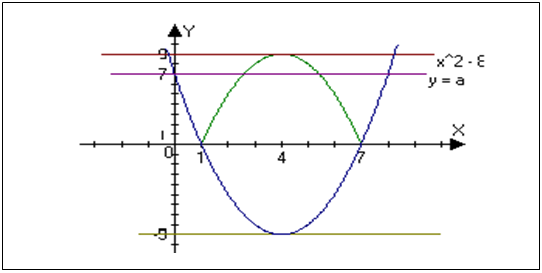
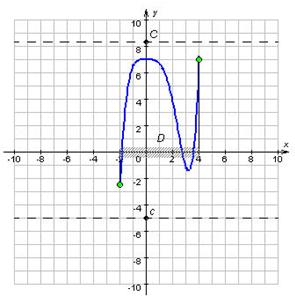
суцільними лініями зображена частина параболи в = ![]() 2 – 8х +
2 – 8х + ![]() (1 < х < 7), отримана дзеркальним відбиттям щодо осі 0х частини параболи
(1 < х < 7), отримана дзеркальним відбиттям щодо осі 0х частини параболи
х2 - 8х + 7 при 1 < х < 7.
(Ескіз лівої частини графіка функції при х < 0 можна одержати, відбивши ескіз правої частини графіка симетрично щодо осі 0у).
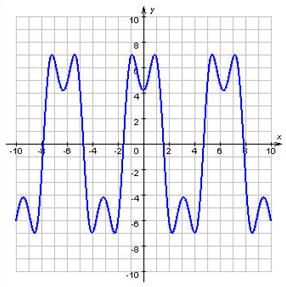
Проводячи горизонталі в = а, а ![]() N, одержуємо k крапок її перетинання з лініями ескізу графіка. Маємо:
N, одержуємо k крапок її перетинання з лініями ескізу графіка. Маємо:
а | 0 | [1; 6] | 7 | 8 | 9 |
|
| к | 4 | 8 | 7 | 6 | 4 | 2 |
Таким чином, а = k при а = 7.
Відповідь: 7.
Похожие работы
... ї інформації уздовж від параметра (див. мал. (??)): Очевидно, що максимальна кількість рішень дорівнює трьом, і це досягається, коли або . Відповідь. . Графічне рішення рівнянь і нерівностей з модулем Рішення рівнянь, що містять знак абсолютної величини часто набагато зручніше вирішувати не аналітично, а графічно (особливо рівняння утримуючі параметри). Побудова графіків виду , і ...
... , тоді й . Отже, для таких х, і, виходить, на цьому проміжку нерівність (11) також не має рішень. Отже, нерівність (11) рішень не має. Відповідь: O. 3 ДЕЯКІ ШТУЧНІ СПОСОБИ РІШЕННЯ РІВНЯНЬ Існують і інші нестандартні методи рішення рівнянь і нерівностей, крім використання властивостей функції. Дана глава присвячена додатковим методам рішення. 3.1 Множення рівняння на функцію І ...
... , рівняння прийме вид: Очевидно, що , для всіх і Отже, останнє рівняння рівносильне системі: Тим самим, ми довели, що при , рівняння має єдине рішення. Відповідь. . тригонометричний рівняння комбінований графічний Рішення з дослідженням функції Приклад [??] Доведіть, що всі рішення рівняння і- цілі числа. Рішення. Основний період вихідного рівняння дорівнює . Тому ...
... ставляться також рівність (1.6) Формули (2.12) і (2.15) доводяться підстановкою в них ряду (1.1) або виводяться на основі вже відомих рекурентних співвідношень для суміжних функцій. 1.3 Гіпергеометричне рівняння Помітимо, що гіпергеометрична функція u= F( , , ,z) є інтегралом лінійного диференціального рівняння z(1-z) +[ -( + +1)] - u=0 (2.16) регулярним в околиці ...
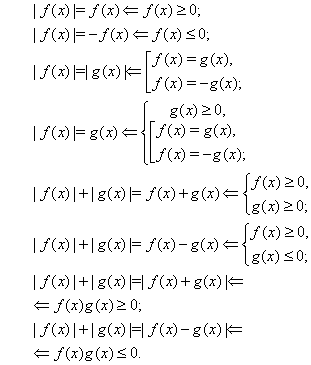

0 комментариев