Навигация
Указати значення параметра а, при якому рівняння
6. Указати значення параметра а, при якому рівняння
х4 + (1 – 2а)х2 + а2 – 4 = 0 має три різних корені.
Рішення: усяке біквадратне рівняння в загальному випадку має дві пари корінь, причому корінь однієї пари різняться тільки знаком. Три корені можливі у випадку, якщо рівняння має одну пару у вигляді нуля.
Корінь заданого рівняння рівні:
х = 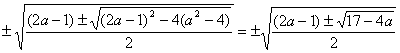
Одна з пар корінь буде дорівнює 0, якщо (2а-1) = ![]() . Вирішуючи це рівняння за умови 2а-1 > 0
. Вирішуючи це рівняння за умови 2а-1 > 0 ![]() >
> ![]() , маємо: (2а – 1) =
, маємо: (2а – 1) = ![]()
![]() (2а – 1)2 = 17 – 4а
(2а – 1)2 = 17 – 4а ![]()
4а2 – 4а +1 = 17 – 4а ![]() а = 2.
а = 2.
Відповідь: 2.
Указати ціле значення параметра p, при якому рівняння
![]() cosx – 2sinx =
cosx – 2sinx = ![]() +
+ ![]() має рішення.
має рішення.
Рішення: р ≥ 0; 2 – р ≥ 0 ![]() р ≤ 2; поєднуючи припустимі значення параметра р, маємо:
р ≤ 2; поєднуючи припустимі значення параметра р, маємо:
0 ≤ р ≤ 2.
При р = 0 вихідне рівняння приймає вид – 2sinх = 2![]()
![]() х належить порожній множині ( у силу обмеженості синуса).
х належить порожній множині ( у силу обмеженості синуса).
При р = 1 вихідне рівняння приймає вид:
cosx-2sinx = ![]() +1.
+1.
Максимальне значення різниці (cosx-2sinx) становить
![]() = (- sinx – 2cosx) = 0
= (- sinx – 2cosx) = 0 ![]() tgx = -2, при цьому sinx =
tgx = -2, при цьому sinx =
sin (arctg(-2)) = ![]() , cosx – 2sinx =
, cosx – 2sinx = ![]() , що менше
, що менше ![]() +1.
+1.
Отже, при р = 1 рівняння рішень не має.
При р = 2 вихідне рівняння приймає вид
![]() .
.
Максимальне значення різниці ![]() становить
становить ![]() при х = arctg(-
при х = arctg(-![]() ) (при цьому sinx =
) (при цьому sinx = ![]() , cosx =
, cosx = ![]() ). Оскільки
). Оскільки ![]() >
> ![]() +1, то рівняння
+1, то рівняння ![]() =
= ![]() буде мати рішення.
буде мати рішення.
Відповідь: 2.
8. Визначити число натуральних n, при яких рівняння ![]() не має рішення.
не має рішення.
Рішення: х ≠ 0, n ? 10.
![]()
![]()

Рівняння х2 – 8х – n(n – 10) = 0 не має рішення, якщо його дискримінант менше 0, тобто 16 + n(n-10) < 0 ![]() n2 -10n +16 < 0
n2 -10n +16 < 0 ![]() (n-2) (n-8) <0
(n-2) (n-8) <0 ![]() 2 < n < 8.
2 < n < 8.
У знайденому інтервалі 5 натуральних чисел: 3, 4, 5, 6 і 7. З огляду на умову n ? 10, знаходимо, що загальне число натуральних n, при яких рівняння не має рішень, дорівнює 6.
Відповідь: 6.
9. Знайти найменше ціле значення параметра а, при якому рівняння
![]() (0 < х <
(0 < х < ![]() ) має рішення.
) має рішення.
Рішення: за умовою 1 > sinx > 0 ![]() 1 <
1 < ![]() < +
< + ![]() ,
,
1 > cosx > 0![]() 1 <
1 < ![]() < +
< + ![]() ,
,
Отже, 2 < а < + ![]() .
.
Зводячи обидві частини заданого рівняння у квадрат, маємо:
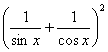 = а2
= а2 ![]()
![]() = а2
= а2 ![]()
![]()
![]() = а2.
= а2.
Уведемо змінну z = ![]() . Тоді вихідне рівняння прийме вид:
. Тоді вихідне рівняння прийме вид:
z2 + 2z – а2 = 0. Воно має рішення при будь-якому а, оскільки його дискримінант
D = 1 + а2 позитивний при будь-якому а.
З огляду на, що 2 < а < + ![]() , містимо, що найменше ціле значення параметра а, при якому задане рівняння має рішення дорівнює 3.
, містимо, що найменше ціле значення параметра а, при якому задане рівняння має рішення дорівнює 3.
Відповідь: 3.
Висновок
Під час створення даного проекту ми вдосконалили свої старі знання по темі «Рівняння з параметрами, зв'язаних із властивостями показовою, логарифмічною й тригонометричною функціями » і якоюсь мірою одержали нові.
По завершенню роботи ми прийшли до висновку, що ця тема повинна вивчатися не тільки на елективних курсах і додаткових заняттях, але й у шкільній програмі, тому що вона формує логічне мислення й математичну культуру в школярів. Учням (студентам) знання по цій темі допоможуть здати незалежне оцінювання знань.
Література
1. П.І.Горнштейн, В.Б.Полонский, М.С.Якир Задачі з параметрами. – К., 2002.
2. Н.Ю.Глаголєва Задачі по математиці для вступників у вузи. – К., 1994р.
3. В.В.Лікоть Задачі з параметрами, - К., 2003р.
4. В.В.Ткачук Математика – абітурієнтові. – К., 1994р.
5. Г.А.Ястребинецький Рівняння й нерівності, що містять параметри. – К., 2004
6. А.Г.Мордкович Алгебра й початок аналізу. – К., 1997р.
Похожие работы
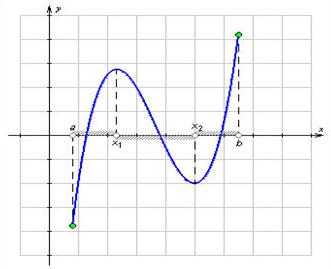
... ї інформації уздовж від параметра (див. мал. (??)): Очевидно, що максимальна кількість рішень дорівнює трьом, і це досягається, коли або . Відповідь. . Графічне рішення рівнянь і нерівностей з модулем Рішення рівнянь, що містять знак абсолютної величини часто набагато зручніше вирішувати не аналітично, а графічно (особливо рівняння утримуючі параметри). Побудова графіків виду , і ...
... , тоді й . Отже, для таких х, і, виходить, на цьому проміжку нерівність (11) також не має рішень. Отже, нерівність (11) рішень не має. Відповідь: O. 3 ДЕЯКІ ШТУЧНІ СПОСОБИ РІШЕННЯ РІВНЯНЬ Існують і інші нестандартні методи рішення рівнянь і нерівностей, крім використання властивостей функції. Дана глава присвячена додатковим методам рішення. 3.1 Множення рівняння на функцію І ...
... , рівняння прийме вид: Очевидно, що , для всіх і Отже, останнє рівняння рівносильне системі: Тим самим, ми довели, що при , рівняння має єдине рішення. Відповідь. . тригонометричний рівняння комбінований графічний Рішення з дослідженням функції Приклад [??] Доведіть, що всі рішення рівняння і- цілі числа. Рішення. Основний період вихідного рівняння дорівнює . Тому ...
... ставляться також рівність (1.6) Формули (2.12) і (2.15) доводяться підстановкою в них ряду (1.1) або виводяться на основі вже відомих рекурентних співвідношень для суміжних функцій. 1.3 Гіпергеометричне рівняння Помітимо, що гіпергеометрична функція u= F( , , ,z) є інтегралом лінійного диференціального рівняння z(1-z) +[ -( + +1)] - u=0 (2.16) регулярним в околиці ...
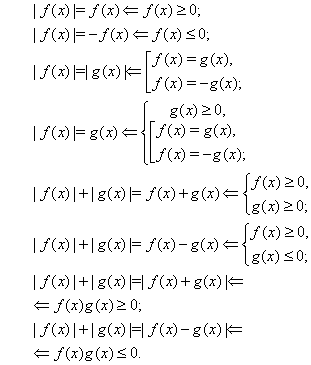
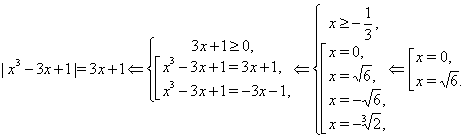

0 комментариев