Дерево мероприятий

8.2 Дерево мероприятий

 

8.2.1. Особенности построения дерева мероприятий

Дерево мероприятий, как мы уже говорили выше, может быть продолжением дерева целей (его следующим уровнем) или строиться как самостоятельное дерево, но после построения дерева целей. С помощью дерева мероприятий может быть решена достаточно сложная проблема, связанная с принятием решения по выбору конкретной стратегии достижения поставленной цели. Причем, детализация этой стратегии (комплекса мероприятий и работ) становится более подробной по мере того, как ветвление дерева мероприятий продвигается вниз по уровням. В верхних уровнях отражаются предварительные или промежуточные мероприятия и только на самом нижнем уровне мы выходим на конкретные работы и операции по реализации данной стратегии (пути) достижения цели. Конкретный путь (стратегия) определяется, конечно, в контексте всей ветви (начиная от верхнего уровня).

Существенным отличием дерева мероприятий от дерева целей является то, что в деревьях мероприятий используется логика ИЛИ (дизьюнкция), т.е. детализация сводится к вычленению альтернативных вариантов действий (нужно принять одно ИЛИ другое ИЛИ третье ИЛИ и т.д.). Следует отметить, что дерево мероприятий имеет много общего (а в некоторых случаях полностью совпадает) с деревом решений, так как каждое ветвление есть принятие решения по выбору той или иной альтернативы действий при решении задачи формирования пути (мероприятия) по достижению цели.

На рис. 8.2 представлено дерево мероприятий для подцели “Встреча Нового года”. Вершины (элементы) этого дерева пронумерованы (цифры слева внизу прямоугольника вершины) и далее веточки альтернатив и сами вершины мы будем рассматривать, используя эти обозначения. Детализацию элементов этого дерева вполне можно продолжать и далее. Например, в элементах дерева 3.1 и 3.2 можно детализировать каких гостей следует пригласить, в 3.5 и 3.6 - кого бы мы хотели (или кого необходимо) пригласить, в 3.7 и 3.8 - указать цель путешествия и т.д. Вот только для решения 3.4, пожалуй, трудно найти дальнейшую детализацию.

Такое дерево дает отличный обзор всего поля альтернативных мероприятий и обеспечивает проверку его полноты. Существует столько вариантов достижения нашей подцели, сколько ветвей в дереве. Основной вопрос состоит в том, как получить такой отличный обзор, если, конечно, поле мероприятий вообще можно представит подобным образом?

Очевидно, для решения такой задачи нужно строить цепочки мероприятий, в которых общность должна снижаться по мере перехода к более низким уровням иерархии. Следовательно, в перечне беспорядочно собранных вариантов мероприятий (первый шаг) неявно уже должна быть заключена некоторая иерархическая система, которую нам надлежит отыскать. Надо в таком ещё беспорядочном наборе образовать группы, классы или найти общие черты, которые можно обнаружить при обобщении понятий. Если при всех стараниях это не получается, значит, задача непригодна для подобного представления.

8.2.2 Семейства в дереве мероприятий

Итак, в общем виде дерево мероприятий представляет обозримый набор множества вариантов достижения поставленной цели. Интересной представляется задача оценки дерева мероприятий для отыскания наилучшего варианта (веточки дерева) набора мероприятий.

Мы уже знаем, что дерево мероприятий (как частный случай дерева взаимосвязей) состоит из элементов (вершин графа) и ветвей (рёбра графа). Теперь мы введём понятие семейства. Семейство дерева мероприятий охватывает какой-нибудь известный элемент и непосредственно с ним связанные элементы нижнего уровня.

В нашем примере о праздновании Нового года имеется 8 семейств (перечисляем вершины):

Номер семейства	Коды вершин
1 2 3 4 5 6 7 8	0, 1.1, 1.2 1.1, 2.1, 2.2 1.2, 2.3, 2.4, 2.5 2.1, 3.1, 3.2 2.2, 3.3, 3.4 2.3, 3.5, 3.6 2.4, 3.7, 3.8 2.5, 3.9

На верхнем уровне надо оценить для каждого семейства “дочерние” элементы, сравнив их с “материнскими”. Для семейства 1 это означает оценить два основных варианта решений: встречать ли Новый год дома или уехать куда-нибудь. Остальные детали не принимаются во внимание.

Для семейства 2 этот вопрос выглядит следующим образом: Как оцениваются альтернативы “с гостями” и “без гостей”, если принято решение остаться дома? Для семейства 3 надо оценить варианты: посещение родных или знакомых, поездку через бюро путешествий и посещение мест общественных увеселений, причём факт самого отъезда следует рассматривать как заданный. Таким же образом продолжается сравнительная оценка оставшихся вариантов.

При оценке предпоследнего семейства исходят из того, что выбрана поездка через бюро путешествий и остается сравнить между собой два возможных варианта (с выездом за рубеж или в пределах родины).

Последнее семейство представляет особый случай. Здесь больше нет разветвлений, значит, нет и необходимости в оценке. Элемент 3.9 практически не отличается от элемента 2.5 и введён только для того, чтобы довести все ветви до одного уровня (исключаем эффект зависания).

8.2.3 Численная оценка дерева мероприятий

Для получения количественных оценок дерева мероприятий необходимо рассматривать различные альтернативы с учетом различных факторов, влияющих на оценку различных мероприятий. Такие факторы, по существу можно трактовать как критерии выбора того или иного варианта. Без этого эффект данного метода пропадает. Здесь можно одновременно учитывать не один, а несколько критериев, причём различного характера. Лучше всего сначала, не выбирая, записать все критерии, определяющие выбор в данной задаче, а затем упорядочить этот список, приписывая каждый набор критериев соответствующему семейству. Как обычно поступают при выборе варианта встречи Нового года? Рассматривают следующие критерии:

·  - денежные расходы;

·  - затраты времени на подготовку;

·  - степень новизны;

·  - ожидаемые впечатления;

·  - возможные отрицательные последствия;

·  - пожелания гостей;

·  - собственные склонности;

·  - встречи (желательные или нежелательные).

Конечно, есть множество и других обстоятельств. Быть может, кое-кто захочет уточнить или исключить тот или иной критерий. Оставим, однако, их в указанном виде.

Было бы, наверное, нецелесообразно и слишком накладно применять все 8 критериев для всех 7 семейств нашего дерева. В дальнейшем мы будем использовать не более 4 критериев одновременно, приспосабливая их к особенностям каждого семейства. Рассматриваемый метод обладает требуемой гибкостью.

Ниже приведен набор таблиц для каждого семейства. В этих таблицах в первом столбце выписаны выбранные для данного семейства критерии, во втором, обозначенном буквой КВ, - весовые коэффициенты, учитывающие важность того или иного критерия для оценки альтернатив данного семейства. Сумма чисел этого столбца должна быть равной единице, то есть весовые коэффициенты критериев должны быть долями единицы. Последующие столбцы содержат оценки предпочтительности для альтернативных вариантов мероприятий (решений) при оценке по каждому критерию. В этих клетках записываются значения оценок, причём сумма по горизонтали должна равняться единице. Это значит, что предпочтение делится между элементами таким образом, что их сумма образует единицу. Более предпочтительные (с точки зрения данного критерия) варианты оцениваются высоко, менее предпочтительные - низко.

Нетрудно видеть, что количественные оценки для рассматриваемых критериев (КВ) и оценки альтернатив по каждому критерию можно получить используя, например, метод экспертных оценок, рассмотренный в предыдущей главе и уже примененный нами для дерева целей.

Рассмотрим более подробно технологию расчета для таблиц семейств, приведенных ниже. Последовательность расчетов можно разбить на следующие этапы:

¨  формирование с помощью экспертов набора критериев (факторов) для оценки альтернатив в предлагаемом дереве взаимосвязей;

¨  выбор с помощью экспертов отдельных групп критериев для конкретных семейств дерева (из сформированного на предыдущем этапе набора);

¨  получение с помощью экспертного опроса коэффицентов важности (КВ) критериев для каждого семейства;

¨  получение с помощью экспертного опроса оценок альтернатив семейства по каждому критерию;

¨  заполнение расчетной таблицы семейства и получение обобщенных численных оценок альтернатив дерева мероприятий.

Первые два этапа связаны с генерацией набора критериев и их анализом. Здесь можно применить технологии экспертного оценивания типа “мозгового штурма”. Дальнейшие этапы требуют уже применения методов экспертного оценивания, позволяющих получить количественные оценки. Мы будем для этих целей продолжать использовать метод ранжирования. При оценке КВ для набора критериев этот метод полностью подходит, так как он позволит получить удельные веса критериев, которые и есть коэффициенты важности или весовые коэффициенты.

Не останавливаясь на этапах формирования набора критериев и их привязки к семействам, рассмотрим порядок расчетов при выполнении остальных этапов. Ниже приведены таблицы расчетов, полученные с помощью Microsoft Excel.

Повторяя эти расчеты для всех критериев и семейств, мы получаем данные для заполнения расчетных таблиц по семействам, которые позволяют получить итоговые веса альтернатив, учитывающие все критерии данного семейства. Ниже приведены таблицы для всех семейств дерева.

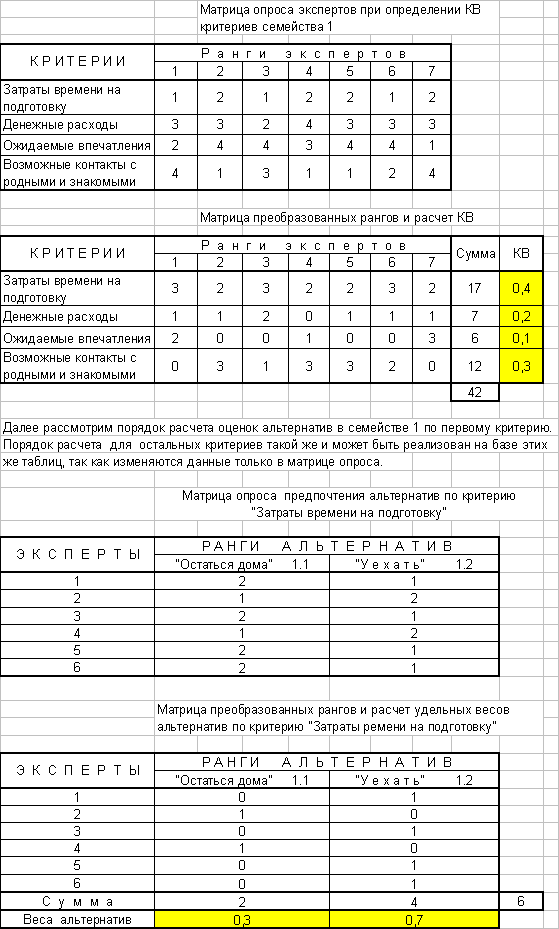
Таблица семейства 1

Критерии	КВ	1.1	1.2	Сумма
Затраты времени на подготовку	0.4	0.3	0.7	1
Денежные расходы	0.2	0.6	0.4	1
Ожидаемые впечатления	0.1	0.1	0.9	1
Возможные контакты с родными и знакомыми	0.3	0.6	0.4	1
Итоговые оценки		0.43	0.57	1

Таблица семейства 2

Критерии	КВ	2.1	2.2	Сумма
Затраты времени на подготовку	0.3	0.2	0.8	1
Денежные расходы	0.2	0.2	0.8	1
Возможные контакты с родными и знакомыми	0.5	1.0	0.0	1
Итоговые оценки		0.60	0.40	1

Таблица семейства 3

Критерии	КВ	2.3	2.4	2.5	Сумма
Степень новизны	0.3	0.1	0.7	0.2	1
Денежные расходы	0.2	0.6	0.1	0.3	1
Ожидаемые впечатления	0.2	0.1	0.7	0.2	1
Возможные контакты с родными и знакомыми	0.3	0.8	0.1	0.1	1
Итоговые оценки		0.41	0.40	0.19	1

Таблица семейства 4

Критерии	КВ	3.1	3.1	Сумма
Собственные желания	0.2	0.2	0.8	1
Денежные расходы	0.2	0.4	0.6	1
Последствия	0.2	0.2	0.8	1
Предполагаемые желания гостей	0.5	0.7	0.3	1
Итоговые оценки		0.49	0.51	1

Таблица семейства 5

Критерии	КВ	3.3	3.4	Сумма
Склонности	0.8	0.6	0.4	1
Денежные расходы	0.1	0.2	0.8	1
Последствия	0.1	0.2	0.8	1
Итоговые оценки		0.52	0.48	1

Таблица семейства 6

Критерии	КВ	3.5	3.6	Сумма
Желания гостей	0.6	0.7	0.3	1
Денежные расходы	0.1	0.5	0.5	1
Последствия	0.3	0.2	0.8	1
Итоговые оценки		0.53	0.47	1

Таблица семейства 7

Критерии	КВ	3.7	3.8	Сумма
Степень новизны	0.4	0.3	0.7	1
Денежные расходы	0.2	0.8	0.2	1
Ожидаемые впечатления	0.4	0.8	0.9	1
Итоговые оценки		0.40	0.60	1

Рассмотрим несколько примеров из этих таблиц:

Семейство 1. Критерий “впечатления” по сравнению с другими критериями имеет наименьший вес (КВ=0.1). Решение 1.1 (“встречать Новый год дома”) дает гораздо меньше оснований ожидать новых впечатлений, чем решение 1.2 (“уехать”). Поэтому для 1.1 получается вес (количественная оценка) 0.1, а для 1.2 - 0.9.

Семейство 2. Критерий “встреча с родственниками и знакомыми” по мнению экспертов наиболее важный из трёх. Поскольку решение 2.2 (“без гостей”) однозначно исключает какие-либо визиты, в соответствующей клетке получается 0. И в этом случае вариант 2.1 логично оценивается единицей.

Семейство 3. Критерий “денежные расходы” (КВ=0.2) менее важен, чем степень новизны и возможные контакты с родными и знакомыми, и располагается на одном уровне с критерием “впечатления”.

Для трёх вариантов 2.3, 2.4 и 2.5 расходы оцениваются соответственно в отношении 1:6:2.

Поездка, организованная бюро путешествий, стоит дороже всего. Однако веса в соответствующих клетках имеют значения 0.6, 0.1 и 0.3. Почему? Да потому, что высокие цены надо рассматривать как недостаток данного варианта, они характеризуют его отрицательно и весовые коэффициенты должны быть низкими. Отсюда проистекает обратный характер зависимости, которая в точности соответствует приведенной выше пропорции (мы уже обращали внимание на то, что в некоторых случаях коэффициенты и сами значения критериев обратны).

Теперь надо рассмотреть последнюю строку оценочной таблички семейства 1, строку сумм. Итоговые оценки для альтернатив 1.1 и 1.2, учитывающие оценки по всем критериям, образуются в результате сложения произведений из оценок альтернатив и весовых коэффициентов соответствующих критериев. По существу, эта итоговая оценка получается как взвешенная сумма..

Итоговая оценка альтернативы 1.1 вычисляется так:

0.4*0.3+0.2*0.6+0.1*0.1+0.3*0.6=0.43.

Для альтернативы 1.2 надо подсчитать следующую сумму

0.4*0.7+0.2*0.4+0.1*0.9+0.3*0.4=0.57.

Сумма по горизонтали в строке итоговых оценок, как и в вышерасположенных строках получается равной 1, что свидетельствует о корректности расчетов..

После того как для всех семейств оценочные таблички будут заполнены, числа, образовавшиеся в строке итоговые оценки альтернатив, надо выписать возле соответствующего элемента на графическом изображении дерева решений. На этом заканчивается первый этап алгоритма оценки. На следующем, втором, этапе остаётся перемножить оценки, стоящие возле элементов дерева и относящиеся к каждой ветви (различные пути от элемента 0 до элементов нижнего уровня, в нашем примере - до элементов 3.1, 3.2, ..., 3.9).

Если при построении дерева решений принять, что каждый элемент (кроме 0) имеет лишь один подчинённый элемент, то есть исключить какие бы то ни было горизонтальные связи, то дерево решений будет иметь ровно столько ветвей, сколько элементов на последнем уровне:

 

Ветвь 1 (0 - 3.1): 0.43*0.60*0.49 = 0.126

Ветвь 2 (0 - 3.2): 0.43*0.60*0.51 = 0.132

Ветвь 3 (0 - 3.3): 0.43*0.40*0.52 = 0.089

Ветвь 4 (0 - 3.4): 0.43*0.40*0.48 = 0.083

Ветвь 5 (0 - 3.5): 0.57*0.41*0.53 = 0.124

Ветвь 6 (0 - 3.6): 0.57*0.41*0.47 = 0.110

Ветвь 7 (0 - 3.7): 0.57*0.40*0.40 = 0.091

Ветвь 8 (0 - 3.8): 0.57*0.40*0.60 = 0.137 Максимум!

Ветвь 9 (0 - 3.9): 0.57*0.19*1.00 = 0.108

Сумма = 1.000

По этим результатам можно непосредственно увидеть ранжированную (по степени важности) последовательность вариантов решений. Наибольшую величину произведения мы находим у элемента 3.8 - поездка за границу, затем следуют:

3.2 - встречать Новый год дома с гостями без танцев;

3.1 - встречать Новый год дома с гостями и танцами;

3.5 - встречать Новый год у родственников или знакомых с танцами;

3.6 - встречать Новый год у родственников или знакомых без танцев;

3.9 - посетить увеселительные заведения;

3.7 - путешествие по своей стране, организованное бюро путешествий;

3.3 - встречать Новый год дома без гостей;

3.4 - тихо в собственной постели во сне “вползти” в Новый год.

На этом заканчивается второй этап этого метода оценки вариантов и дерево мероприятий выполнило поставленную перед ним задачу. Оценки альтернатив, очевидно, можно выразить и в процентах, поскольку их сумма составляет 1.0. Для этого достаточно соответствующие десятичные дроби умножить на 100.

На первый взгляд, этот метод оценки выглядит весьма основательным. К сожалению, это не совсем так. Чтобы результаты в итоге были действительно сравнимы, метод должен непременно удовлетворять следующим двум условиям:

·  число ветвлений на каждом уровне должно быть одинаковым;

·  каждая ветвь должна быть доведена до самого нижнего уровня, а не обрываться раньше.

Первое условие требует того, что за каждым элементом одного какого-нибудь уровня должны следовать всегда два или три элемента более низкого уровня. Второе условие требует, чтобы ветвление, в соответствии с первым условием, продолжалось до тех пор пока не будет достигнут последний уровень решения. Оба условия являются кардинальными. Однако даже в нашем небольшом примере они не выполняются. Крайняя правая ветвь (0 - 3.9) доведена до самого нижнего уровня только искусственно. По существу она заканчивается на элементе 2.5. Первое условие не удовлетворяется поскольку:

·  на втором уровне встречается два и три дочерних элемента;

·  на третьем уровне имеем по два дочерних элемента и один раз встречается один дочерний элемент.

Это означает, что результаты будут не совсем точными и, строго говоря, не отражают действительного соотношения значимости 9 вариантов возможных решений. Однако, можно утверждать, что эти недостатки не имеют решающего значения и не обесценивают сам метод. Этим методом можно пользоваться, если:

·  попытаться еще на стадии первоначального построения дерева мероприятий по возможности полнее удовлетворить упомянутые два условия;

·  в случае отклонения результатов от идеального вида не абсолютизировать их. При оценке этих результатов не стоит игнорировать возможные ошибки.

При некотором навыке можно оценить, где эти ошибки становятся заметными и где следует внести коррективы. Кроме того, существуют чисто математические приемы позволяющие скорректировать результаты для случая дерева не удовлетворяющего основным условиям.

8.3 Вопросы для самопроверки

1.   Что такое дерево мероприятий, поле вариантов альтернативных мероприятий (решений) ?

2.   Понятие "семейства" в дереве мероприятий.

3.   Критерии (факторы) при оценке альтернативных вариантов.

4.   Порядок численной оценки альтернативных вариантов.

5.   Весовые коэффициенты и порядок их применения.

6.   Исчисление весов отдельных ветвей дерева мероприятий.

7.   Порядок выбора наиболее эффективного варианта.

8.   Условия получения надёжных оценок при анализе дерева мероприятий.

9. МЕТОДЫ СЕТЕВОГО ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ

 

В предыдущих главах были рассмотрены методы, позволяющие расчленять сложные проблемы на составные части и разрабатывать комплексы работ и мероприятий для разрешения, как составных частей, так и всей проблемы в целом. Целью данной главы является рассмотрение методов логично дополняющих рассмотренные ранее методы и позволяющих разработать эффективные расписания (планы) выполнения всех работ (мероприятий), необходимых для разрешения проблемы. Эти методы позволяют ответить на вопрос: что делать и в какой последовательности, чтобы работы были выполнены в срок и с минимальными затратами ресурсов.

9.1 Основные понятия и определения   9.1.1 Возникновение и становление метода

Мы уже говорили о том, что сложную систему можно представить сетью или графом. При этом узлы графа соответствуют отдельным блокам (элементам, подсистемам), а дуги, соединяющие эти узлы, будут указывать на связи или зависимости между блоками.

Анализ правильно выбранной и построенной сетевой модели очень часто помогает составить достаточно ясное представление о системе и её функционировании. Общее изучение систем на основе сетевого анализа приобретает всё возрастающее значение.

В последние десятилетия сетевые модели стали широко использоваться для описания во времени последовательностей работ, выполняемых при реализации сложных проектов. В нашей стране методы, реализующие эти подходы, называют методами сетевого планирования и управления (СПУ), причём, сфера их применения непрерывно расширяется. Особенно широкое распространение получили эти методы, начиная с середины 50-х годов, за рубежом. В США наиболее часто они используются под названиями СРМ (английская аббревиатура, означающая метод критического пути) и PERT (Programme Evaluation and Review Technique – метод оценки и обзора программ). Система СРМ была впервые применена при управлении строительными работами, система PERT – при разработке системы “Поларис”. В последнее время за рубежом эти методы чаще называют методами управления проектами.

Применение сетевых методов планирования и управления расширялось с невероятной быстротой при реализации масштабных проектов в области строительства крупных объектов, эксплуатации заводов, организации больниц, проектирования зданий, в области космических полетов и т.п. Последовательность выполнения работ в любом проекте, большом или малом, от взятия пробы лунного грунта до чистки пары ботинок может быть успешно описана и проанализирована с помощью сетевой модели.

Системы СПУ представляют такие системы управления, в которых объектом управления является коллективы исполнителей, располагающих определёнными ресурсами и выполняющими комплекс операций, призванных обеспечить достижение намеченного конечного результата. СПУ основано на моделировании процесса с помощью сетевого графика и представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ.

Система СПУ позволяет:

¨  формировать календарный план реализации некоторого комплекса работ (мероприятий);

¨  выявлять и мобилизовывать резервы времени, трудовые, материальные и денежные ресурсы;

¨  осуществлять управление комплексом работ по принципу “узкого места” (“ведущего звена”) с прогнозированием и предупреждением возможных срывов в ходе работ;

¨  повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.

Процесс построения и использования сетевой модели включает три основных этапа: этап планирования, этап анализа и этап управления.

9.1.2 Основные определения

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (мероприятий), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Главными элементами сетевой модели являются работы и события.

Работа. В сетевой модели весь комплекс операций расчленяется на отдельные операции (работы), располагаемые в строгой технологической последовательности. Сетевой график представляет собой изображение на плоскости хода выполнения проекта.

Термин работа может иметь следующие значения:

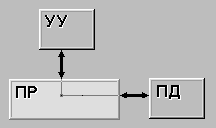
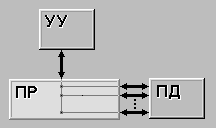
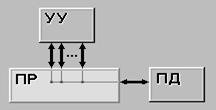
*  действительная работа в прямом смысле слова, то есть трудовой процесс, требующий затрат времени и ресурсов;

*  ожидание, не требующее затрат труда, но занимаемое некоторое время (например, процесс затвердения бетона);

*  “фиктивная” работа, то есть логическая связь между двумя или несколькими операциями, не требующая ни затрат времени, ни ресурсов, но указывающая, что возможность начала одной работы непосредственно зависит от результатов другой работы.

Пример 9.1

Задание. Вскипятить чайник с водой. Множество работ:

a1 - наполнить чайник водой:

a2 - поставить чайник, наполненный водой, на плитку, включить её и ждать, пока он не закипит.

Ясно, что работа a1 должна быть закончена, прежде чем начнётся работа a2.

Пример 9.2

Задание. Приготовить чашку растворимого кофе с молоком. Множество работ:

a1 - вскипятить воду (как в предыдущем примере);

a2 - вскипятить молоко (эта процедура аналогична a1);

a3 - положить в чашку ложечку растворимого кофе;

a4 - добавить одновременно соответствующее количество молока и воды.

В этом примере последовательность работ во времени не так очевидна, как в первом случае. Если мы предположим, что существуют две конфорки, то работы “вскипятить молоко” и “вскипятить воду” можно выполнять одновременно. Если же в наличии имеется только одна конфорка, то эти работы необходимо выполнять последовательно. Работу a3 можно выполнять только после того, как и молоко и вода вскипят; очевидно, также, что работа a4 не может быть начата до тех пор, пока все работы a1, a2 и a3 не будут окончены.

Замечания:

1. В общем случае разбиение большой программы (плана) на множество работ не единственно. Например, работы “вскипятить воду” или “вскипятить молоко” могут быть разбиты при желании на более мелкие работы. Выбор множества работ для некоторого плана зависит от необходимого уровня анализа. Очень часто первое разбиение бывает грубым, при этом ориентируются на основные действия процесса. Дальнейшее разбиение направлено на выявление зависимостей внутри групп работ, соответствующих более низкому уровню деятельности.

2. Работа может соответствовать заданию, выполнение которого сопряжено с определёнными усилиями; наоборот, работа может быть бездеятельной, например, ожидание чего-то, что должно произойти (для рассмотренного примера это будет ожидание кипения воды).