Иногда в множество работ полезно включить фиктивную работу. Это работы, которые не занимают времени и для которых не используются никакие ресурсы

3. Иногда в множество работ полезно включить фиктивную работу. Это работы, которые не занимают времени и для которых не используются никакие ресурсы.

4. Имеется несколько специальных случаев, зависимостей между работами, которые должны быть рассмотрены при построении сетевых моделей (например, параллельное выполнение работ, зависимость одной работы от нескольких предшествующих и т.п.).

Событие. Очевидно, что если какая-либо работа может быть начата только после окончания нескольких определённых работ, то необходимым и достаточным исходным условием для её начала являются лишь сумма частных результатов этих работ, то есть их суммарный результат. Этот суммарный результат и принято называть термином событие. Событие означает точку во времени, которая отделяет различные стадии осуществления проекта.

Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним – начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ. Среди событий сетевой модели выделяют начальное и конечное события. Начальное событие не имеет предшествующих работ и событий, относящихся к рассматриваемому в модели комплексу работ. Конечное событие не имеет последующих работ и событий.

Пример 9.3

В задании “вскипятить чайник воды” (пример 9.1) мы можем выделить три точки времени, которые называются событиями:

*  - время начала выполнения задания (начальное событие);

*  - время, когда мы ставим чайник на конфорку после завершения работы “наполнить чайник”;

*  - время начала кипения, характеризующее конец выполнения задания (конечное событие).

Существует два основных вида графического представления расписаний (графиков) работ. Это сетевые графики и диаграммы Ганта. Мы вначале рассмотрим графическое представление в виде классических сетевых графиков (опираясь на упоминавшуюся выше теорию графов), а в конце главы продемонстрируем представление возможные модификации сетевых графиков, а также представление расписаний в виде диаграмм Ганта.

Графическое изображение событий и работ. В сетевых графиках работы обычно изображаются стрелками (т.е. направленными дугами) графа. Действительные работы изображаются на сетевом графике сплошными стрелками, а фиктивные работы - пунктирами. Описания работ при желании могут записываться вдоль стрелок. События должны быть занумерованы. Как правило, вершины графа обозначаются некоторыми геометрическими фигурами (например, кружочками). Внутри этих фигур проставляется соответствующий номер. Описание события может быть тоже записано внутри кружочка.

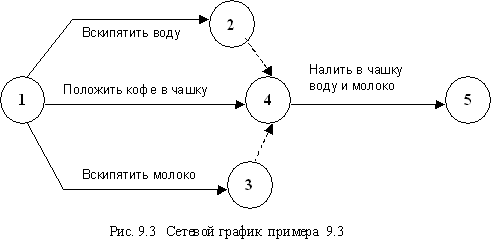
Работа должна быть выполнена в течение времени между двумя событиями, обозначенными своими номерами в концах соответствующей стрелки. Событие, соответствующее началу стрелки, называется начальным (или предшествующим) событием; конец стрелки называют конечным (или последующим) событием. Любая работа может быть определена своими числами, которые соответствуют начальным и конечным событиям.

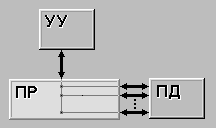
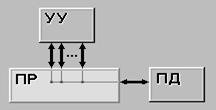
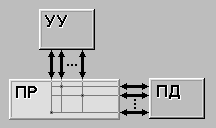
На рис. 9.1 - 9.3 иллюстрируются графические изображения сетей.

Замечания

1. Фиктивные работы (время выполнения равно нулю) необходимы для изображения параллельных работ. Три параллельные работы – “вскипятить воду”, “вскипятить молоко”, “положить в чашку кофе” - имеют одни и те же начальные и конечные события; для большей ясности события 2 и 3 (которые соответствуют событию 4) показаны на графике. Фиктивные работы 2 - 4 и 3 - 4 обозначены пунктиром.

2. Длина стрелок и расположение дуг не имеют значения.

3. Желательно придерживаться следующих правил:

*  время изменяется слева направо;

*  конечным событиям всегда присваиваются большие номера, чем соответствующим начальным событиям. (Числа не обязательно должны подчиняться естественному порядку 1, 2, 3, На практике часто используются числа с промежутками между ними, например, в сетевой модели “Приготовить чашку кофе” этими числами могли быть 1, 5, 6, 7, 10.)

Основная работа и отношения между событиями. При составлении сети необходимо принимать во внимание следующее:

*  - событие нельзя считать наступившим (или достигнутым), если все работы, ведущие к этому событию, не окончены;

*  - работа не может быть начата до тех пор, пока начальное событие данной работы не наступило.

Например, в сети на рис. 9.3 мы находим, что событие 4 не может быть достигнуто, пока не будут достигнуты события 2 и 3 и работы 1-2, 1-3 и 1-4 не будут окончены. Далее, как видим, работа 4-5 не может быть начата, пока событие 4 не будет достигнуто.

Продолжительность работы. После того как конечное множество работ задано и сеть проекта нарисована, необходимо оценить продолжительность выполнения каждой работы, которая должна быть подписана под соответствующей стрелкой.

Продолжительность работы есть время ее выполнения. Заметим, что это не то же самое, что время между начальным и конечным событием. Например, начальное и конечное события некоторой работы могут происходить в 3-й и 7-й день соответственно, тогда как продолжительностью работы может быть только один день; в таком случае мы говорим, что работа имеет резерв в три дня. Вопросы резерва работ будут рассмотрены далее.

Пример 9.4

Задание. Покрасить дверь (один маляр и один помощник).

Список работ (в скобках указана их продолжительность в минутах):

a1 - счистить старую краску (75);

a2 - прошкурить дверь (30);

a3 - открыть банку и размешать краску (4);

a4 - приготовить кисти (5);

a5 - вытереть дверь (4), сделать до a6;

a6 - покрасить дверь (15);

a7 - вычистить кисти и собрать инструменты (6).

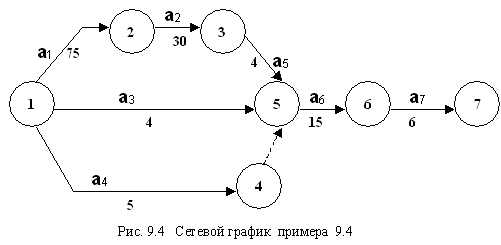
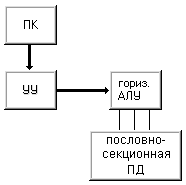
Сетевая модель этого проекта изображена на рис.9.4.

Разбиение проекта на множество работ и определение связей между работами во времени - задача весьма трудоемкая. Ее решение помогает выявлению промежуточных целей и направления действий, которым должен следовать руководитель. Это дает возможность решить, какие работы должны быть выполнены для осуществления различных подпроектов, позволяет правильно распределить все работы. После построения сетевой модели ход действий становится ясным и можно приступить к выполнению проекта; другими словами, сетевое планирование предусматривает выработку некоторой стратегии действий.

При решении задачи планирования может быть извлечена дополнительная информация из сетевой модели самого плана. Это приводит нас к стадии анализа, в котором такие понятия, как критический путь и резерв времени работы, играют ключевую роль.

Критический путь. Первый шаг в анализе графа работ заключается в нахождении критического пути (или путей) сети. Для определения этого понятия мы рассмотрим простейшую сеть, изображенную на рис. 9.5.

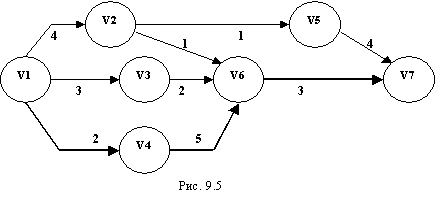
Замечания. В наших примерах мы не будем обсуждать реального смысла работ, как это делалось в предыдущих примерах и упражнениях. Как правило, вся символика будет той же, что на рис. 9.5. Символом V (вершина) обозначаются события; пара (Vi, Vj) определяет работу aij; число, стоящее около каждой стрелки, означает время выполнения соответствующей работы.

В сети на рис. 9.5 V1 означает начало проекта, а V7 - его окончание. Заметим, что от вершины V1 к вершине V7 можно пройти по сети четырьмя различными путями; для каждого пути мы можем определить его временную продолжительность - длину пути, т.е. сумму продолжительностей последовательных работ, образующих путь. Пути и их продолжительности будут следующими.

Путь Продолжительность

V1 - V2 - V5 - V7 4 + 1 + 4 = 9

V1 - V2 - V6 - V7 4 + 1 + 3 = 8

V1 - V3 - V6 - V7 3 + 2 + 3 = 8

V1 - V4 - V6 - V7 2 + 5 + 3 = 10

Определения:

1. Максимальное значение в множестве продолжительностей всех путей (оно может достигаться на нескольких путях) называется полным временем осуществления проекта. Это значение определяет наикратчайшее время, за которое может быть выполнен весь проект.

Похожие работы

Исследование функционирования системы управления на примере ОАО "Камышинпищепром"

Скачать

59301

0

0

... структура управления компанией направлена прежде всего на установление четких взаимосвязей между ее отдельными подразделениями, распределение между ними полномочий и ответственности. В ней реализуются различные требования к совершенствованию системы управления, находящие выражение в тех или иных принципах управления. Организационные структуры управления фирмами отличаются большим разнообразием и ...

Значение математических приемов статистического исследования в современных условиях

Скачать

58380

0

0

... математическая лучше всего представлена в [2,4]. По историческим причинам основные российские работы публикуются в [3]. Обзор современного состояния статистики математической дан в [6]. Статистика объектов нечисловой природы - раздел математической статистики, в котором статистическими данными являются объекты нечисловой природы, т.е. элементы множеств, не являющихся линейными пространствами. ...

Международные маркетинговые исследования. Услуги современных агентств международных маркетинговых исследований

Скачать

15004

2

0

... так, чтобы он был наиболее удобен для внешних рынков, удалённых респондентов. Полученная информация кодируется, анализируется, делаются выводы. III             Услуги современных агентств маркетинговых исследований Проведение международных маркетинговых исследований (исследования действительно международных товаров), зарубежных исследований (исследования, выполняемые в другой стране, а не в ...

Исследование архитектуры современных микропроцессоров и вычислительных систем

Скачать

133942

0

27

... ; -            показывать, за счет каких структурных особенностей достигается увеличение производительности различных вычислительных систем; с этой точки зрения, классификация может служить моделью для анализа производительности. 1.12 Классификация Дазгупты Одним из последних исследований по классификации архитектур, по-видимому, является работа С. Дазгупты, вышедшая в 1990 году. Автор ...