Навигация
Методы и модели линейного программирования
2. Методы и модели линейного программирования.
Фирма производит два безалкогольных широко популярных напитка " Колокольчик" и "Буратино". Для производства 1 л. " Колокольчика требуется 0, 002 ч работы оборудования, а для " Буратино" – 0,04 ч, а расход специального ингредиента на них составляет 0,01 кг и 0, 04 кг на 1 л соответственно. Ежедневно в распоряжении фирмы 16 кг специального ингредиента и 24 ч работы оборудования. Доход от продажи 1 л
" Колокольчика" составляет 0,25 руб., а " Буратино" – 0,35 руб.
Определите ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи.
Решение:
1) Составим математическую модель данной задачи:
Пусть X1 – количество " Колокольчиков";
Х2 – количество " Буратино", тогда как необходимо определить ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи, то целевая функция:
F(Х1,Х2) = 0,25Х1+ 0,35Х2![]() мах
мах
Система ограничений:

xj![]()
2) Графическое решение задачи:
Представим каждое неравенство в виде равенства, т.е имеем уравнения прямых. Построим их, тогда система ограничений запишется в виде:
1) 0,02х1+0,04х2=24
2) 0,01х1+0,04х2=16
3) х1=0
4) х2=0
Преобразуем систему неравенств ( выразим Х2 через Х1)
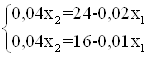
![]()

Построим на плоскости ( х1,х2) область допустимых значений согласно системе неравенств
x2=24-0,5x1
| х1 | 0 | 20 |
| х2 | 24 | 14 |
х2=16-4х1
| х1 | 0 | 4 |
| х2 | 16 | 0 |
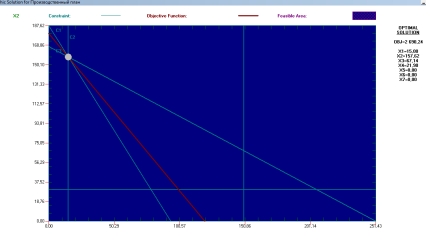
Многоугольником допустимых решений является треугольник АВС. Построим вектор N = ![]()
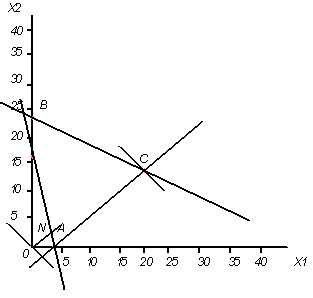
Перемещаем линию уровня перпендикулярно вектору N в направлении вектора N до опорного положения.
Вершина в которой целевая функция принимает максимальное значение это вершина
С (20;13). Следовательно, ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от продажи составляет:
f(х1;х2)= 0,25*20+0,35*13=9,55
3) Классификация математической модели:
· По общему целевому назначению: прикладная модель;
· По степени агрегирования объектов: микроэкономическая модель;
· По конкретному предназначению: оптимизированная модель;
· По типу информации: идентифицированная модель;
· По учету фактора времени: статистическая модель;
· По учету фактора неопределенности: детерминированная модель;
· По типам математического аппарата: линейная модель;
· По типу подхода к изучаемым социально- экономическим системам: нормативная модель.
Вывод: Ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от продажи составляет 9,55 л.
Похожие работы
... математической статистики. Если в собранных эмпирических материалах (анкетах, результатах экспериментов) проявляется действие статистических закономерностей, то применение методов теории вероятностей и математической статистики в конкретном социально-правовом исследовании для анализа и обработки полученных материалов не только желательно, но и необходимо. Для социологии права значительный интерес ...
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
... понятие теории понятие множества не подлежит логическому определению. Элементы множества могут иметь самую различную природу. Например, можно говорить о множестве микросхем, входящих в определенную конструкцию РЭА, или о множестве чертежей, входящих в полный комплект конструкторской документации для производства какого-либо изделия, и т. д. Множества обозначают заглавными буквами латинского ...
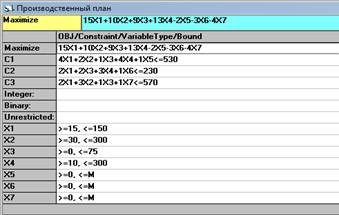
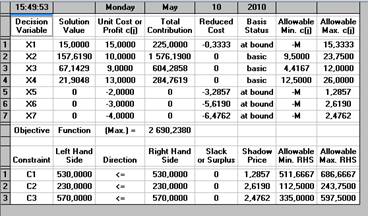
... : Ресурсы А В С D Наличие Ресурс R1 4 2 1 4 530 Ресурс R2 2 - 2 3 230 Ресурс R3 2 3 1 - 570 Прибыль 15 10 9 13 Нижн. гр. 15 30 0 10 Верхн. гр. 150 300 75 300 Построим математическую модель задачи, обозначив количество выпускаемых изделий через х1, х2, х3, х4, а целевую функцию (валовую маржинальную прибыль) — через F: F(х) = 15х1 + 10х2 + 9х3 + ...
0 комментариев