Навигация
3. Помилкова точність
теорія ймовірностей біологічна мінливість
Калькулятори, що стали в останні роки повсюдно доступними, безсумнівне благо, що, однак, має і негативні сторони. Чи всі розуміють, скільки цифр потрібно залишати при множенні і розподілі на калькуляторі, якщо він показує їхній вісьмох чи навіть дванадцять? І майже всі студенти і навіть аспіранти вважають, що залишати їхній потрібно якнайбільше. Це невірно! Розберемо найпростіший приклад.
Обмірюваний радіус окружності дорівнює 6 м. Знайти її довжину.
Звичайно розраховують: З=2p=2x3,14x6 м=37,68 м. Але чотири вірні цифри - це дуже висока точність, у соті частки відсотка, що не так вуж часто реалізується при вимірах. Відкіля взятися такої високої точності, якщо хоча б одна величина, що входить у формулу, дана з точністю, на кілька порядків меншої? Адже в нашому прикладі вона виражається всього однією цифрою. Так що коректна відповідь такий: довжина окружності " 38 м. А якщо необхідний дійсно точна відповідь, те і дані в умові задачі повинні бути з відповідним числом знаків, скажемо 6,00 м.
Правила округлення проходять у середній школі. Вони приведені в багатьох книгах, наприклад у класичному "Довіднику по математиці для інженерів і втузів, що учиться," И. Н. Бронштейна і К. А. Семендяева. Але якось так вийшло, що зараз цей маленький розділ (у всякому разі, у курсі математики) школярам не викладають і вуж поготів не згадують у курсах вищої математики у вузах. Ще років двадцять назад учні й інженери широко користалися логарифмічною лінійкою, що давала точність у двох чи три значущі (тобто вірні) цифри й автоматично захищала обчислювача від фіктивної (іноді говорять - ілюзорної) точності, навіть якщо він забував правила округлення. Але рахункову лінійку витиснув технічний прогрес, захист зникла, і "ефект удаваної точності" придбав масштаби епідемії.
Щоб знизити його вплив, потрібно випливати класичним правилам округлення. У них основним поняттям служить число значущих цифр, що відноситься тільки до вимірюваних, тобто випадковим величинам. Воно вважається ліворуч праворуч починаючи з першої ненульової цифри. Наприклад, 0,004080 має чотири, а 4,08x10-3 - три значущі цифри. множник, що має 10 у кратному ступені, не впливає на число значущих цифр, а лише вказує обраний масштаб величини, не приводячи при цьому до фіктивної точності. Ще приклад. Відстань 3,5 км= 3,5x103 м - точна рівність, у якому ліворуч і праворуч по двох значущі цифри. Не так просто обстоїть справа з рівністю 3,5 км= 3500 м. Якщо це усього лише приведення масштабу до інших кратних одиниць - одна справа. Якщо ж треба відбити безпосередній результат виміру - трохи інше. Адже праворуч коштують чотири значущі цифри, а ліворуч їхній дві; тому, відбиваючи результат, краще ставити хвилястий знак наближеної рівності. Неважко відчути різну інформаційну і навіть економічне навантаження в частинах рівності. Число ліворуч має абсолютну точність 50-100 м, а праворуч - 0,5-1 м, від половини до цілого останнього "розподілу". Якщо така висока точність дійсно потрібна при вимірі кілометрових відстаней, то цінність цього результату і вартість його виміру набагато вище, ніж у числа ліворуч.
Нагадаємо головне правило округлення: якщо роблять чи множення розподіл, то в результаті залишають стільки цифр, скільки їхній містить найменш точна з обмірюваних величин, і звичайно зберігають ще одну запасну цифру. Помітимо, що часто плутають число значущих цифр із числом десяткових знаків, вважаючи, що якусь роль грає положення коми в числі. Але кома лише вказує на прийнятий масштаб вимірів і не задає числа значущих цифр. Наприклад, 1,205 км= 1205 м; і в тім і в іншому випадку число значущих цифр дорівнює і, отже, вони записані з однаковою точністю.
Оборотний увага на одні несподівані труднощі. Виявляється, у дуже багатьох навчальних книгах по математиці приведені приклади, у яких точність вимірювальних даних в умові на кілька порядків нижче, ніж точність у рішенні. Точність як би здатна виникати нізвідки, і це міцно осідає в підсвідомості учнів. Приведу тільки один приклад з добротного у всіх інших відносинах "Керівництва до рішення задач по теорії ймовірностей і математичній статистиці" В. Е. Гмурмана.
Імовірність появи події в кожнім з 100 незалежних іспитів постійна і дорівнює р=0,8. Знайти імовірність того, що подія з'явиться не менш 75 разів і не більш 90 разів.
Сама задача вирішена в принципі, зрозуміло, правильно. Але точність результату записана чотирма цифрами: шукана імовірність дорівнює 0,8882, тоді як правильної був би запис 0,89.
Запис у задачнику має на увазі точність у соті частки відсотка. Відкіля з'являється така точність, якщо в умові імовірність 0,8 задана тільки однією значущою цифрою і тому характеризується точністю в десятки відсотків? Повчально згадати досвіди видатного статистика К. Пирсона: коли симетрична монета підкидалася 12 тисяч разів, то частота падіння її на герб була 0,5012, а коли 24 тисячі разів - 0,5005 (див. "Наука і життя" № 7, 1993 р.). ми бачимо, що навіть при настільки великому числі повторень досвіду невипадковими стають у першому випадку лише дві цифри, а в другому з натяжкою їхній три. У більшості ж інших видів механічних іспитів число повторень набагато нижче, нижче і точність результатів.
- Ну і що? - запитаєте ви. - чи Треба займатися такими дріб'язками, начебто б особливих неприємностей від збереження зайвих цифр не виникає.
Це не так. І не просто тому, що взагалі при аналізі спостережень людина повинна прагнути до істини, а омани можуть завдати шкоди, навіть якщо заздалегідь не завжди ясно який. По-перше, якщо не знати, як правильно округлити результат, на якій цифрі зупинитися, те де гарантія, що ви не відрізаєте і вірні цифри, погіршивши необхідну точність? По-друге, допустимо, ви зберегли зайві, незначні цифри, а результат потрібно збільшити в дуже велике число раз. Тоді випадковий "довесок" чи "недовагомий" приведе до великої помилки, який можна було б уникнути (така ситуація типова для астрономічних задач). По-третє, якщо в якісь документи (опису, звіти, протоколи іспитів) потраплять незначні цифри, неможливо буде в точності відтворити вихідні величини. Одним словом, освоїти нескладні правила округлення випадкових величин усе-таки випливає.
Висновок
Події, що спостерігаються нами, (явища) можна підрозділити на наступні три види: достовірні, неможливі і випадкові.
Достовірним називають подія, що обов'язково відбудеться, якщо буде здійснена визначена сукупність умов S. Наприклад, якщо в судині міститься вода при нормальному атмосферному тиску і температурі 20°, то подія «вода в судині знаходиться в рідкому стані» є достовірне. У цьому прикладі задані атмосферний тиск і температура води складають сукупність умов S.
Неможливим називають подія, що свідомо не відбудеться, якщо буде здійснена сукупність умов S. Наприклад, подія «вода в судині знаходиться у твердому стані» свідомо не відбудеться, якщо буде здійснена сукупність умов попереднього приклада.
Випадковим називають подія, що при здійсненні сукупності умов S може або відбутися, або не відбутися. Наприклад, якщо кинута монета, то вона може упасти так, що зверху буде або герб, або напис. Тому подія «при киданні монети випав «герб»—випадкове. Кожна випадкова подія, зокрема випадання «герба», є наслідок дії дуже багатьох випадкових причин (у нашому прикладі: сила, з яким кинута монета, форма монети і багато хто інші). Неможливо врахувати вплив на результат усіх цих причин, оскільки число їхній дуже велике і закони їхньої дії невідомі. Тому теорія ймовірностей не ставить перед собою задачу пророчити, відбудеться одинична чи подія ні, — вона просто не в силах це зробити.
По-іншому обстоїть справа, якщо розглядаються випадкові події, що можуть багаторазово спостерігатися при здійсненні тих самих умов S, тобто якщо мова йде про масові однорідні випадкові події. Виявляється, що досить велике число однорідних випадкових подій незалежно від їхньої конкретної природи підкоряється визначеним закономірностям, а саме вірогідним закономірностям. Установленням цих закономірностей і займається теорія ймовірностей.
Отже, предметом теорії ймовірностей є вивчення вірогідних закономірностей масових однорідних випадкових подій.Знання закономірностей, яким підкоряються масові випадкові події, дозволяє передбачати, як ці події будуть протікати. Наприклад, хоча, як було вже сказане, не можна наперед визначити результат одного кидання монети, але можна пророчити, причому з невеликою погрішністю, число появ «герба», якщо монета буде кинуте досить велике число раз. При цьому передбачається, звичайно, що монету кидають у тих самих умовах. Методи теорії ймовірностей широко застосовуються в різних галузях природознавства і техніки: у теорії надійності, теорії масового обслуговування, у теоретичній фізиці, геодезії, астрономії, теорії стрілянини, теорії помилок спостережень, теорії автоматичного керування, загальної теорії зв'язку й у багатьох інших теоретичних і прикладних науках. Теорія ймовірностей служить також для обґрунтування математичної і прикладної статистики, що у свою чергу використовується при плануванні й організації виробництва, при аналізі технологічних процесів, попереджувальному і приймальному контролі якості продукції і для багатьох інших цілей.
В останні роки методи теорії ймовірностей усе ширше і ширше проникають у різні області науки і техніки, сприяючи їхньому прогресу.
Список використаної літератури
1. Вентцель Е.С., Овчаров Л. А. Теория вероятностей и ее инженерные приложения. - М.: Гл.ред. ФМЛ, 2007. - 480 с.
2. Мостеллер Ф., Рурке Р., Томас Дж. Вероятность. – под ред. И.М. Яглома. – М., Издательство «Мир», 2009. – 426 с.
3. Груман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 5-е перераб. И доп. М., «Высшая школа», 1999.
4. Венцель Е.С., Теория вероятностей, М., «Наука», 2004.
5. Розанов Ю.А., Лекции по теории вероятностей, М., «Наука», 2008.
Похожие работы
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... ів на 1000 народжених у середньому приходиться 511 хлопчиків і 489 дівчаток; ця вражаюча постійність народження дівчаток і хлопчиків відмічалась багатьма вченими, серед яких був і один із засновників теорії ймовірностей – французький математик Сімон Лаплас ( 1749-1827). Проглядаючи у свій час списки народжень по Парижу за 1745-1784 роки. Лаплас виявив, що відношення хлопчиків до загального числа ...
... Метод моментів Метод моментів є одним із методів точечного оцінювання параметрів розподілу. Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів 1,2,…,k. Це означає, що відомий вид функції щільності fx(х, ), де = (1,2,…,k), якщо X безперервна (відомий вид функції ймовірності Р (X= х,), якщо X дискретна), але числові значення k параметрів не відомі. ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
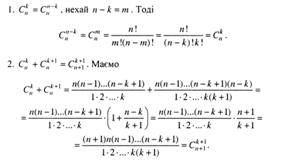
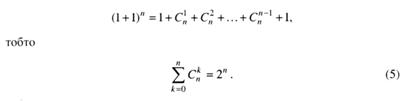


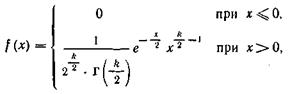
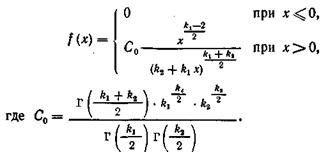

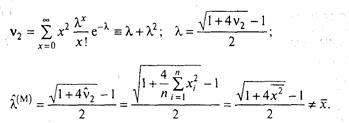
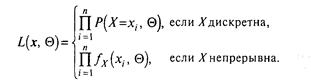
0 комментариев