Лема про рукостискання

1.2 Лема про рукостискання

Формулювання цієї леми просте – „кількість рук, що приймають участь у рукостисканні N-пар людей, дорівнює 2*N”. Лему можна представити у формі графу, де N вершин з’єднані ребрами d(x_i,x_j) рукостискання i та j – вершин (див. рис.1.12), виконавши наступне доведення.

Рис.1.12. „Лема про рукостискання” 5 осіб у вигляді графу „взаємно-простягнутих рук” (10 пар рук для повної множини рукостискань) [3]

Нехай  граф з множиною верщин . Тоді

 (1.1)

Доведення. Зауважимо,що кожне ребро графа в сумі  враховується двічі (див. рис.1.5), і тому спараведива рівність (1.1). Зауважимо, що сума сту-пенів усіх вершин у графі (або мультіграфі без петель) повинна бути парною. Це випливає з того, що якщо взяти вершини, взагалі не пов'язані одна з одною, то сума ступенів цих вершин дорівнює нулю. Додаючи будь-яке ребро, що пов'язує дві вершини, збільшуємо суму всіх ступенів на 2 одиниці. Таким чи-ном, сума всіх ступенів вершин парна. З рівності 1.1 випливає такє твердження: число вершин непарного степеня в графі обовязково є парним числом.

Для визначення матриці суміжності, розглянемо граф . Нехай

Означення 1.7.

Матриця називається матрицею суміжності ( інцидентності) графа .

Матриця суміжності - це симетрична матриця, елементи якої до-рівнюють нулеві або одиниці ( діагональні елементи дорівнюють нулеві) і така, що сума чисел в будь-якому рядку і будь-якому стовпці дорівнює степені від-повідної вершини. Так, для графу, наведеного на рис.1.13, матриця суміжності побудується у вигляді:

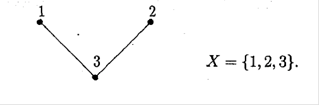
Рис.1.13. До побудови матриці суміжності 3-х вершинного графу

Означення 1.8.

Послідовність ребер, в якій сусідні ребра інцидентні одній і тій же вершині називаються ланцюгом. Ланцюг називається простим, якщо всі вершини, належні йому (крім, можливо, першої і останньої), різні; число в цьому випадку називають довжиною ланцюга.

Якщо  , то ланцюг називається циклом. Цикл, в якому всі вершини різні, називається простим. Приклади простих ланцюгів та простих циклів наведені на рис.1.14:

(1,3), (3,4), (4,6) – простий ланцюг;

(1,2), (2,5), (5,6) – простий ланцюг;

(1,3), (3,4), (4,6), (6,5), (5,2)Ю (2,1) – простий цикл.

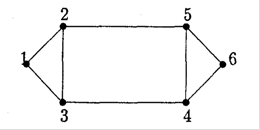
Рис 1.14. Приклад графа з простими ланцюгами та простими циклами

Означення 1.9.

Граф є підграфом графа , якщо .Якщо  , то підграф  називається остовним підграфом.

Означення 1.10.

Граф  є сумою графів , якщо

ця сума називається прямою, якщо ,

1.3 Оцінки для числа ребер з  компонентами зв ‘язності

Означення 1.11.

Граф називається зв язним , якщо будь-які вершини  та   сполучені ланцюгом з початком в  і кінцем в . З симетрії випливає, що в цьому випадку і вершина  сполучена з вершиною .

Теорема 1.2.

Кожен граф є прямою сумою зв язних графів.

Доведення. На множині вершин  граф визначимо відношення

, якщо  сполучається з  .Відношення  є відношенням еквівалентнос-ті. Позначимо через .Тоді  і є розбиття  на класи еквівалентності. Графи  є зв язними графами і

 (1.2)

є прямою сумою зв’язних графів.

Ці графи називаються компонентами зв’язності.

Розглянемо оцінки для числа ребер з  компонентами зв’язності.

Теорема 1.3.

Нехай граф, який складається з  вершин,  ребер і компонент зв язності. Тоді виконуються нерівності

Доведення . Доведемо спочатку нерівність .Будемо доводити індукцією за числом ребер. Припустимо, що нерівність справедлива для всіх графів з числом ребер . Нехай граф з вершин,  ребер і

компонентами зв’язності. Викреслимо максимальне можливе число ребер так, щоб не змінювалося число компонент зв’язностя. Число ребер в отриманому графі позначемо .

Розглянемо для прикладу граф, зображений на рисунку (1.15)

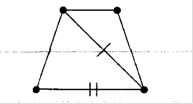
Рис. 1.15. Приклад 1 графу для оцінки зв’язності

В ньому .Викресливши два ребра, отримаємо граф . Викреслити далі яке-небудь ребро, не порушуючи зв язності, вже не можна (див.рис.1.16).

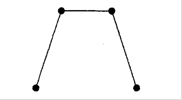
Рис. 1.16. Приклад 1 графу для оцінки зв’язності

Повернемося до графу, отриманого з . Викресливши в ньому ще одне ребро, ми отримаємо граф з числом компонент зв язності на одиницю більшим. В силу індуктивного припущення, справедливого, бо , маємо  , звідки .

Для доведення верхньої оцінки в нерівності (1.3) замінимо кожну компо-ненту повним графом. Нехай  та  два повних, отриманих з компонент зв’ язності  та  , а  та  число ребер в цих компонентах . Замінемо  на повний граф, додавши одну вершину, а  замінемо на повний граф, віднявши одну вершину. Тоді загальне число вершин не змінеться, а число ребер збільшиться на додатню величину

Отже, для того, щоб число ребер у графі було максимально можливим (при фіксованих  і ), граф повинен складатись з  ізольованих вершин і повного графа з  вершинами.Звідси й випливає нерівність (1.3). Теорема доведена.

З нерівності (1.3) випливає такий наслідок.

Наслідок. Будь-який граф з  і більше ніж  ребрами є зв’язним.

Справді, якщо граф з  вершинами має дві компоненти зв’язності, то максимальне число ребер не перевищує .

Найти компоненти сильної зв’язності графу на рис.1.17.

Відповіді

Рис.1.17. 7-ми вершинний граф для обчислення компонентів зв’язності [10]