Орієнтовані графи, графи з петлями, графи з паралельними дугами

1.4 Орієнтовані графи, графи з петлями, графи з паралельними дугами

Дамо означення орієнтованих графів, графів з петлями та графів з пара-лельними дугами.

Неформально, граф виглядає як діаграма, тобто множина точок площини (вершин, або вузлів), з’єднаних між собою лініями (ребрами). Діаграма дає уяву про зв’язки між елементами (вершинами), але нічого не каже про метричні властивості (довжина ліній, їх форма тощо).

Залежно від типу ребер відрізняють кілька типів графів. Петля — це реб-ро, що з’єднує вершину саму з собою. У мультиграфі петлі не допускаються, але пари вершин можуть з’єднуватися кількома ребрами, які називаються крат-ними, або паралельними. У псевдографі допускаються петлі й кратні ребра. В звичайному графі немає ні петель, ні кратних ребер.

За допомогою графів подаються структурні залежності між елементами, відповідний граф називається орієнтованим, або орграфом, а його орієнтовані ребра — дугами. Граф, що має орієнтовані та неорієнтовані ребра одночасно, називається змішаним.

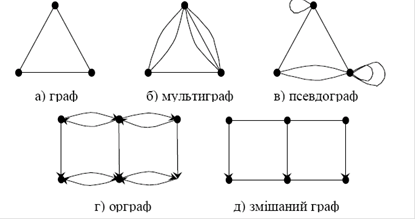
Рис.1.18. Види орієнтованих графів

Означення 1.12.

Нехай  множина вершин ,  - множина впорядкованих пар елементів з  ( будемо називати їх дугами).Орієнтованим графом  називатимемо пару множин  , де .

Дуга  називається дугою з  в  (див.рис.1.19).

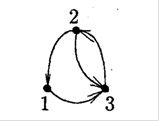
Рис. 1.19. Орієнтований 3-х вершинний граф (,

.)

Теорема 1.4. Число усіх орієнтованих графів з  вершинами дорівнює .

Доведення . Справді , число впорядкованих пар елементів з  дорівнює , тому число всіх можливих множин дуг дорівнює .

Означення 1.13.

Нехай -множина вершин. Орієнтованим графом з петлями будемо називати пару множин , де  (див.рис.1.20).

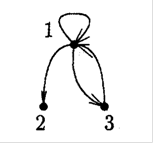
Рис.1.20. Орієнтований граф з петлями в якому ,

Теорема 1.5. Число орієнтованих графів з петлями , які мають  вершин, дорівнює .

Доведення. Справді, число різних множин (підмножин множини ) дорівнює .

Якщо розглядається одночасно декілька типів графів, то графи які описуються означення (1.1), будемо називати простими графами.

Якщо в означенні (1.1) до множини  невпорядкованих пар приєднати ще множину всіх пар виду , то відповідний граф називається простим графом з петлями.

З теореми 1.5 випливає довід теореми 1.6 про прості графи.

Теорема 6. Число всіх простих графів з  вершинами і петлями дорівнює

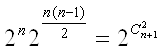
Надалі, ми будемо розглядати прості графи.

РОЗДІЛ ІІ ОЙЛЕРОВІ ГРАФИ