Ойлерова ломиголовка «Кенігзберзьких мостів»

2.1 Ойлерова ломиголовка «Кенігзберзьких мостів»

Для рішення серйозних математичних задач математик Ойлер(Euler) використовував наочні ломиголовки. Одна з них поклала початок зовсім новій області досліджень, що виросла згодом у самостійний розділ математики - теорію графів і топологію. Особливість цієї теорії - у геометричному підході до вивчення об'єктів. Теорія графів – одна з небагатьох математичних дисциплін, дата народження якої може бути встановлена абсолютно точно. Перша робота з теорії графів належить Леонарду Ойлеру. Вона з’явилась в публикаціях Санкт-Петербургзської Академії наук у 1736 році. Праця Ойлера розпочиналася з розгляду однієї ломиголовки так званої „задачі про кенігзберзькі мости” Місто Кенігзберг (нині Калінінград) розташоване на берегах річки Прегель і двох островах. Різні частини міста сполучені сімома мостами. Щонеділі жителі міста любили здійснювати прогулянки по місту. Ойлер поставив питання: чи можна здійснити прогулянку, вийшовши з дому і повернувшись до нього , таку , щоб по кожному мосту пройти рівно один раз. Сформулюємо задачу, як задачу теорії графів. Схематична карта міста зображена на рисунку 2.1..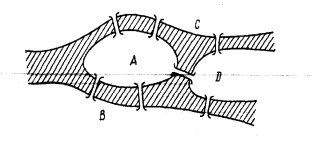

Рис. 2.1. Схема мостів в Кенігзберзі [11]

Чотири частини міста зображені літерами  Оскільки нас цікав-лять лише переходи через мости, ми можемо вважати  вершинами графа, ребра якого відповідають мостам. Цей граф зображено на рисунку 2.2.

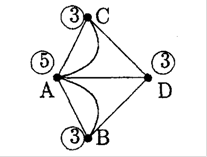
Рис. 2.2. Граф «Кенігзберзьких мостів» в ломи головці Ойлера

Ойлер зауважив, що цей граф не являє єдиного циклу; з якої б вершини ми не почали б обхід , ми не можемо обійти весь граф і повернутись назад, не проходячи жодного ребра двічі. Якби такий цикл існував, то з кожної вершини виходило б стільки ребер , скільки в неї входить , інакше кажучи степінь кожної вершини була б парним числом. Таким чином, відповідь на питання Ойлера-негативна.

Виклавши розв язання задачі про кенігзберзькі мости , Ойлер в своїй праці поставив питання : на яких графах можна знайти цикл, який містить всі ребра графа, при чому кожне ребро зустрічається в циклі рівно один раз?

Це дало початок системному математичному підходу до побудови та вивчення властивості графів.

2.2 Основні поняття та означення ойлерових графів

 

Означення 2.1

Зв’ яний граф називається ойлеровим графом, якщо існує замкнений ланцюг, який проходить через кожне ребро.Такий ланцюг будемо називати ойлеровим ланцюгом, або ойлеровим циклом (див.рис.2.3)

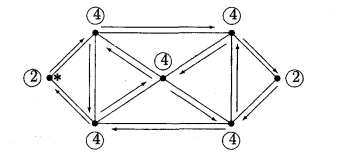
Рис.2.3. Структура вершин та ребер в неорієнтованому ойлеровому графі (* - означено точку входу ойлерового ланцюга - циклу)

Означення 2.2

Граф називається напівойлеровим, якщо існує ланцюг , який проходить через кожне його ребро рівно один раз (див рис.2.4).

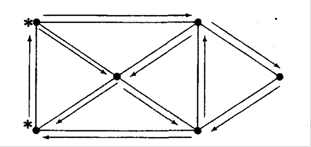
Рис.2.4. Структура вершин та ребер в неорієнтованому напівойлеровому графі (* - означено точку початку та кінця ойлерового ланцюгу)

Рис.2.5. Приклад неойлерового графу

Дослідивши структуру неойлерового графу, наведеного на рис.2.5, розг-лянемо необхідні і достатні умови для того, щоб граф був ойлеровим. Доведемо лему, яка далі буде грати істотну роль.

Лема 2.1

Якщо степінь кожної вершини графа  не менше двох , то граф містить цикл.

Доведення. Якщо в графі є петлі або кратні дуги, то твердження леми оче-видне. Тому надалі будемо припускати , що  є простим графом. Нехай – довільна вершина графа . Побудуємо по індукції маршрут

обираючи вершину , суміжну з , а при  обираючи вершину , суміж-ну з  і відмінну від  (існування такої вершини випливає з умови леми). Оскільки  має скінченне число вершин, то врешті-решт ми прийдемо до вершини , з якої вийшли. Отримаємо цикл

Лема доведена.

Теорема 2.1 Для зв’язного графа  наступні умови еквівалентні:

1.  - ойлерів граф;

2.  кожна вершина  має парний степінь;

3.  множину ребер графа  можна розбити на прості цикли.

Доведення.

Нехай - ойлерів цикл графа . Будемо рухатись по циклу . Проходження кожної вершини збільшує степінь кожної вершини на 2, і оскільки кожне ребро входить в  рівно раз , то будь-яка вершина має парний степінь .

Оскільки  - зв’язний граф , степінь кожної вершини дорівнює принаймні 2; тому в силу леми 2.1 містить простий цикл . Виключимо ребра циклу , отримаємо остовний підграф , в якому кожна вершина має парний степінь. Якщо  немає ребер , то (3) доведено. В протилеж-ному випадку застосуємо проведені вище міркування до , отримаємо граф , в якому степені всіх вершин є парними і так далі. Одночасно з порожнім графом  ,  отримаємо розбиття множини ребер на  циклів

 Нехай множину ребер можна розбити на прості цикли. Нехай  – один з простих циклів. Якщо складається тільки з цього циклу , то -ойлерів граф. В протилежному випадку існує інший простий цикл, який має вершину  , спільну з . Ланцюг, який розпочинається з  і складається з циклу  і наступного за ним циклу , є замкненим ланцюгом, який містить всі ребра графа , кожне один раз . Отже , - ойлерів граф.

З теореми 2.1 випливає наступна теорема.

Теорема 2.2. Зв’язний граф є ойлеровим тоді і тільки тоді, коли кожна його вершина має парний степінь.

.

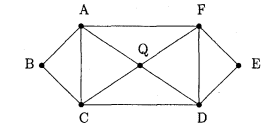
Рис.2.6. Приклад ойлерового графу в теоремі 2.2

Доведення. Граф зображений на рисунку 2.6. є ойлеровим, оскільки

1.  Степінь вершин А, F, D, C, Q = 4(парні);

2.  Степінь вершин B, E = 2(парні);

3.  Множина ребер цього графа є об’ єднання двох простих циклів

 і .

Теорема 2.3. Зв’язний граф є напівойлеровим тоді і тільки тоді , коли в ньому не більше двох вершин непарного степеня.

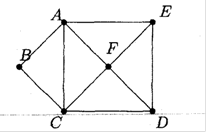
Рис. 2.7. Приклад напівойлерового графу до теореми 2.3

Доведення. Граф зображений на рисунку 2.7. є нпівойлеровим, оскільки

1.  Степінь вершин А, F, C = 4(парні);

2.  Степінь вершин B = 2(парна);

3.  Степінь вершин E,D = 3(непарна);

4.  Ось один з можливих варіантів обходу . Початковою точкою маршрута є точка , а кінцевою є точка .

Якщо граф має дві вершини з непарними степенями (див.рис.2.7), то для будь-якого напіойлерового ланцюга одна з цих вершин буде початковою, а дру-га кінцевою. Для доведення досить сполучити відрізком вершини з непарними степенями.

Зауважимо , що згідно з «лемою про рукостискання» - число вершин непарного степеня є парним.

Спробуємо для довільного графа вказати найменше число ланцюгів та-ких, що жодні два не мають спільних ребер і всі вони повністю накривають ра-зом весь граф. Очевидно, якщо на графі є таке сімейство ланцюгів , то кожна вершина непарного степеня повинна бути або початковою, або кінцевою вер-шиною якогось ланцюга. Загальне число вершин з непарним степенем згідно з лемою про рукостискання є парним, скажімо рівним . Таким чином, кожне сімейство ланцюгів, які накривають граф , повинно містити принаймні  лан-цюгів.

Доведемо, що існування  вершин з непарним степенем є і достатньою умовою існування ланцюгів, які накривають граф.

Теорема 2.4. На будь-якому зв’язному графі з  вершинами непарного степеня існує сімейство ланцюгів, які в сукупності містять всі ребра графа в точності один раз кожне.

Доведення. Позначимо вершини з непарними степенями

Якщо ми додамо до нашого графу ребра

то всі вершини отриманого графа будуть парними і на ньому знайдеться ойле-рів цикл . При відкиданні доданих ребер цикл  розпадеться на  окремих ланцюгів , які містять всі ребра графа.

Граф , зображений на рисунку 2.8 має чотири вершини з непарним степе-нем  і накривається двома ланцюгами  і

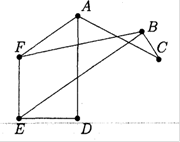
Рис.2.8. Граф з непарним степенем вершин до теореми 2.4

В розважальній математиці ось уже впродовж декількох століть розгляд-даються задачі, які можна сформулювати як задачу пошуку певних маршрутів в графах, зокрема, пошуку ойлерових циклів.

Так, граф на рисунку 2.9. називається «шаблею Магомета», а ойлерів цикл необхідно побудувати за маршрутом, не відриваючи пера ручки від рисунку за одним разом ( тобто розчерком), викреслити фігуру, подану на рис.2.9.

Рис. 2.9. Ойлерів цикл в графі – «Шабля Магомета»

Більшість збірників математичних задач з розважальної математики містять задачі про лабіринти. Лабіринт складається з коридорів та їх перех-ресть. Отже , він може бути зображений графом, в якому ребра відповідають коридорам, а вершини – перехрестям.

Ойлеровим графом повинен бути і план огляду будь-якої виставки, і вздовж приміщень виставки потрібно розставити покажчики обходу таким шля-хом, щоб кожен експонат був оглянутий рівно один раз.

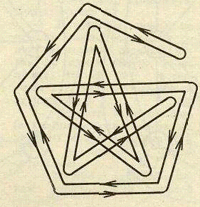
Рис.2.10. Застосування апарату ойлерових циклів при розв’язанні задач “маршрут виставки» [3]

Припустимо, що експонати розташовані з обох сторін шляху, який про-ходить територією виставки. Виявляється, що тоді, яким би не був відповідний граф ( або лишень він був зв’язний), можна провести відвідувача так, щоб кож-ний шлях був пройдений двічі - по одному разу в кожному напрямі (див.рис.2.10).

Теорема 2.5. В зв’язному графі існує орієнтований цикл, який проходить через ребро по одному разу в кожному з двох напрямів.

Доведення.

Сформулюємо загальне правило побудови ланцюга, який проходить взовж всіх ребер графа в точності по одному разу в кожному напрямі. Розпоч-немо з довільної вершини  і пройдемо вздовж , відзначивши це ребро маленькою стрілкою в точці , яка показує вибраний напрям. Потім перехо-димо послідовно до інших вершин. Одній й ті ж вершини можна відвідувати і декілька раз. Кожного разу , потрапивши в якусь вершину, ми будемо ставити на відповідному ребрі стрілку, яка вказує напрям прибуття. Крім того, потрап-ляючи в якусь вершину вперше, ми як-небудь відзначимо вхідне ребро, щоб потім його можна було відрізнити від інших.

А1

А0

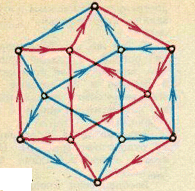
Рис.2.11. Граф до теореми 2.5 [3]

Виходячи з вершини , ми завжди будемо обирати ще невикористаний напрям: або ребро, по якому ми зовсім не проходили, або ребро помічене стріл-кою, яка вказує на те, що ми по ньому вже були. Домовимось також, що тільки тоді , коли у нас немає вибору, ми використаємо для виходу ребро, яким впер-ше прийшли в цю вершину.

Будемо продовжувати шлях до тих пір, коли це взагалі можливо .В кож-ній вершині є однакове число можливостей для входу і для виходу. Тому рух може закінчитися лише в точці . Залишається перевірити , що у всіх верши-нах всі ребра будуть пройдені в обох напрямах.

Для точки  це ясно-всі ребра, які виходять , будуть використані, оскіль-ки в протилежному випадку ми могли б рухатися далі ; тому і всі ребра , які входять, також будуть використані, бо їх число дорівнює числу ребер, які ви-ходять. Зокрема, ребро  буде пройдено в обох напрямках. Але це означає , що всі ребра , які інцидентні , також будуть пройдені в обох напрямах, бо перше ребро, яке входить в , ребро  , за умовою, повинно використову-ватися для виходу лише в останню чергу. Теж саме міркування можна застосу-вати до наступного ребра  і наступної вершини  і так далі.

Отже, в усіх вершинах , які будуть досягнуті, всі ребра виявляться прой-деними в обох напрямах. Оскільки наш граф є зв’язним, це означає, що він буде повністю обійденим.

Зауважимо, що описаний метод обходу графа може бути використаний для розв’язання задач , пов’язаних з пошуками маршрутів виходу з лабіринтів.