Навигация
1.2.4 Показатели сезонности
Сезонными колебаниями называются более или менее устойчивые внутригодовые колебания, уровни развития социально-экономических явлений, проявляются они с различной степенью интенсивности во всех сферах жизни. Характеризуются сезонные колебания индексами сезонности (Is), совокупность которых образуют сезонную волну. Индексом сезонности называется средняя, исчисленная из процентных отношений, по одноименным месяцам фактических уровней к уровням выровненным.
Для выявления сезонных колебаний обычно берутся данные за несколько лет, распределенные обычно по месяцам. Несколько лет берутся для того, чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года.
Для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития можно использовать формулу:
интервал абсолютный прирост динамика
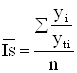 , (1.2.4.1)
, (1.2.4.1)
где: yi – фактические уровни;
yti – теоретические (выравненные) уровни;
n – число лет.
Если ряд не содержит ярко выраженной тенденции в развитии, то индексы сезонности исчисляются по эмпирическим данным без их предварительного варьирования.
Тогда формула расчета будет следующая:
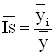 , (1.2.4.2)
, (1.2.4.2)
где: ![]() – общий для анализируемого ряда динамики средний уровень.
– общий для анализируемого ряда динамики средний уровень.
1.3 Показатели вариации
Вариацией признаков называется наличие различий в численных значениях признаков у единиц совокупности явлений. Существует пять обобщающих показателей вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратичное отклонение, коэффициент вариации.
Размах вариации – абсолютная величина разности между максимальными и минимальными значениями:
![]() ,
(1.3.1)
,
(1.3.1)
где: R – размах вариации;
![]() – максимальное значение изучаемого признака;
– максимальное значение изучаемого признака;
![]() – минимальное значение изучаемого признака.
– минимальное значение изучаемого признака.
Среднее линейное отклонение от средней представляет собой среднюю арифметическую из абсолютных отклонений конкретных вариантов от их среднего значения:
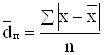 ;
; 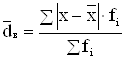 , (1.3.2а, б)
, (1.3.2а, б)
где: ![]() – для первичного ряда;
– для первичного ряда;
![]() – для вариационного ряда.
– для вариационного ряда.
Дисперсия, или средний квадрат отклонений рассчитывается по формулам:
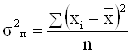 ;
; 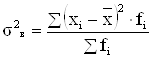 .
(1.3.3а, б)
.
(1.3.3а, б)
Среднее квадратическое отклонение от средней высчитывается по формуле:
![]() . (1.3.4)
. (1.3.4)
Коэффициенты вариации:
![]() ;
; ![]() .
(1.3.5а, б)
.
(1.3.5а, б)
Кроме рассмотренных показателей имеются другие показатели, которые характеризуют структуру рядов распределения, например мода и медиана.
Мода – это значение признака, наиболее часто встречающееся в изучаемых явлениях.
Мода в интервальных рядах высчитывается по формуле:
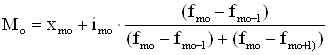 , (1.3.6)
, (1.3.6)
где: Мо – мода;
xmo– нижняя граница модального интервала[1];
imo – величина модального интервала;
fmo – частота соответствующая модальному интервалу;
fmo-1 – частота предшествующая модальному интервалу;
fmo+1 – частота интервала следующего за модальным.
Медиана – величина, которая делит численность упорядоченного ряда на 2 равные части, одна имеет значение варьирующего признака меньше чем средний вариант, а другая больше.
Медиана в интервальных рядах высчитывается по формуле:
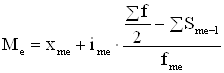 , (1.3.7)
, (1.3.7)
где: Me – медиана;
xmе – нижняя граница медианного интервала[2];
Sf – сумма частот ряда;
SSme-1 – сумма частот, накопленная до медианного интервала;
Fme – частота медианного интервала.
Наряду с медианой для более полной характеристики структуры изучаемого явления применяют квартили. Квартили делят ряд по сумме частот на 4 равные части. Вторым квартилем является медиана. Формулы для остальных квартилей в интервальном ряду имеют вид:
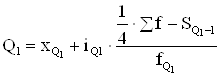 ;
; 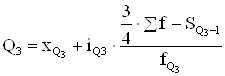 , (1.3.8)
, (1.3.8)
где: xQ1 и xQ3 – нижние границы соответствующих квартильных интервалов[3];
iQi – величина соответствующего интервала;
SQ1-1 и SQ3-1 – накопленные частоты интервалов, предшествующих соответствующим квартильным;
fQ1 и fQ3 – частоты соответствующих квартильных интервалов.
Квартильное отклонение считается по формуле:
![]() . (1.3.9)
. (1.3.9)
Относительный показатель квартильной вариации:
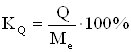 . (1.3.10)
. (1.3.10)
Коэффициент осцилляции:
![]() . (1.3.11)
. (1.3.11)
Для сравнительного анализа степени асимметрии рассчитывают показатель асимметрии:
![]() , (1.3.12)
, (1.3.12)
где: m3 – центральный момент 3го порядка.
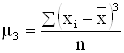 ,
, 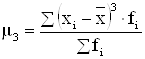 .
(1.3.13а, б)
.
(1.3.13а, б)
Степень существенности этого показателя оценивается с помощью средней квадратичной ошибки:
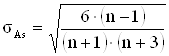 . (1.3.14)
. (1.3.14)
Если 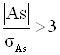 , то асимметрия существенна.
, то асимметрия существенна.
Для симметричных распределений рассчитывается показатель эксцесса:
![]() , (1.3.15)
, (1.3.15)
где: m4 – центральный момент четвертого порядка.
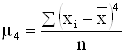 ;
; 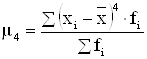 .
(1.3.16а, б)
.
(1.3.16а, б)
Средняя квадратичная ошибка эксцесса рассчитывается по формуле:
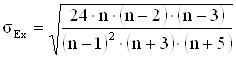 . (1.3.17)
. (1.3.17)
Если 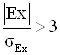 , то эксцесс существенен.
, то эксцесс существенен.
Похожие работы
... и иных внеоборотных активов; - уплаченные штрафы и пени за нарушение налогового законодательства, осуществляемые за счет чистой прибыли предприятия; Глава II. Анализ производства и реализации продукции СПК «Скуратовский» 2.1. Технико-экономическая характеристика предприятия. Общество с ограниченной ответственностью промышленно-коммерческая фирма СПК «Скуратовский» был зарегистрирован 14 ...
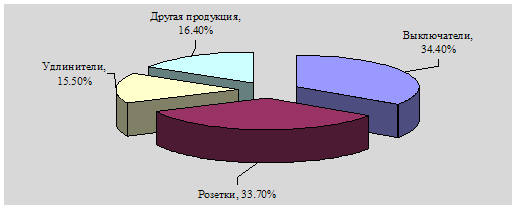
... Структура произведенной ЧУП "Светоприбор" за 8 мес. 2008 г. продукции по плану Рисунок 4. Структура произведенной ЧУП "Светоприбор" за 8 мес. 2008 г. продукции фактически При изучении деятельности предприятия важен анализ ритмичности производства и реализации продукции. Ритмичность - равномерный выпуск продукции в соответствии с графиком в объеме и ассортименте, предусмотренных планом. ...
... проведения самого анализа. 3.2 Анализ структуры и динамики расходов на реализацию товаров Проведем анализ расходов на реализацию товаров Столбцовского райпо. Расходы анализируемой организации характеризуются следующими данными (таблица 3.1) Таблица 3.1 Информация об издержках обращения розничной торговли Столбцовского райпо за 2002/2003 гг. Показатели Годы. Отклонение (+; -) Темп ...
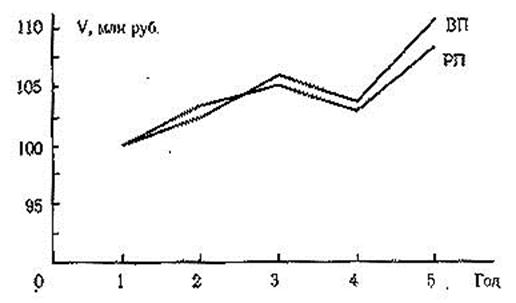
... , квалификации рабочих, аритмичность производства и др. 5 АНАЛИЗ РИТМИЧНОСТИ РАБОТЫ ПРЕДПРИЯТИЯ При изучении деятельности предприятия важен анализ ритмичности производства и реализации продукции. Ритмичность — равномерный выпуск, продукции в соответствии с графиком в объеме и ассортименте, предусмотренных планом. Ритмичная работа является основным условием своевременного выпуска и ...





0 комментариев