Навигация
Средние показатели динамики
55661
знак
18
таблиц
9
изображений
3.2.2 Средние показатели динамики
Среднемесячный выпуск продукции вычислим по формуле (1.2.2.1а):
м2.
Вычислим средний абсолютный прирост на основе цепных приростов по формуле (1.2.2.2):
м2.
Вычислим средний темп роста по формуле (1.2.2.3):
.
Рассчитаем средний темп прироста по формуле (1.2.2.4):
.
Среднемесячный выпуск продукции в 1 полугодии 2010 года составил 120184,4м2. Исходя из рисунка 3.2.2.1 можно сделать вывод, что в 1 квартал продукция производилась в объемах меньших, чем средний выпуск, а во 2й квартал в больших. Ежемесячное увеличение выпуска составило 10799,1м2, т.е. объем производства увеличивался на 11,3% каждый месяц, а средний темп роста составил 1,113.
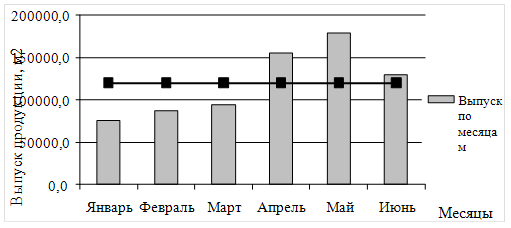
Рисунок 3.2.2.1 – Графическое отображение выпуска продукции по месяцам и среднего выпуска продукции
3.2.3 Сглаживание колеблемости в рядах динамики
Проведем сглаживание колеблемости на основе данных из таблицы 1 приложения А. Возьмем данные о суммарном выпуске продукции за 31 день в течение первого полугодия и занесем их в таблицу 1 приложения Б.
Метод укрупнения интервалов.
Проведем сглаживание колеблемости методом укрупнения интервалов, преобразуя данные, суммируя их по 10-дневкам. В результате получим таблицу 3.2.3.2.
Таблица 3.2.3.2 – Выпуск продукции за полгода по 10-дневкам.
| 10 дневки | Выпуск продукции, м2 |
| 1 | 259697,1 |
| 2 | 259953,1 |
| 3 | 201455,9 |
Полученные данные представим графически на рисунке 3.2.3.1.
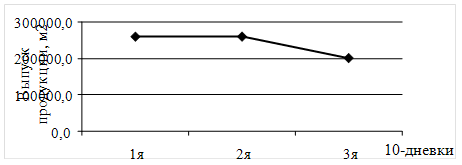
Рисунок 3.2.3.1 – Выпуск продукции по 10-дневкам в 1 полугодии 2010 года
Метод скользящей средней.
Проведем сглаживание на основе таблицы 1 приложения Б методом скользящей средней на основе 10-дневок, т.е. на основе 10 уровней ряда. Воспользуемся формулой (1.2.3.1) и полученные данные занесем в таблицу 2 приложения Б. Полученные данные отобразим графически на рисунке 3.2.3.2.
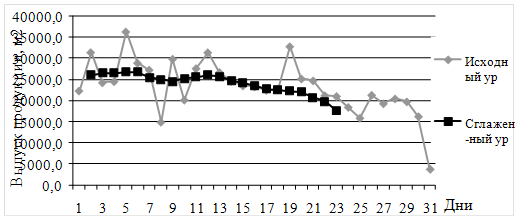Рисунок 3.2.3.2 – Графическое отображение сглаживания уровней
Аналитическое выравнивание ряда.
Проведем аналитическое выравнивание ряда на основе таблицы 1 приложения Б различными функциями.
Рассмотрим выравнивание по прямой. Т.к. количество уровней нечетное, то значения t возьмем от –15 до 15, включая 0. Заполним таблицу 1 приложения В. На основании формул (1.2.3.3а, б) рассчитаем параметры а0 и а1:
; 
.
В результате, используя формулу (1.2.3.2) получим уравнение:
.
На его основе заполнена графа 
в таблице 1 приложения В.
Полученные данные отобразим графически на рисунке 3.2.3.3.
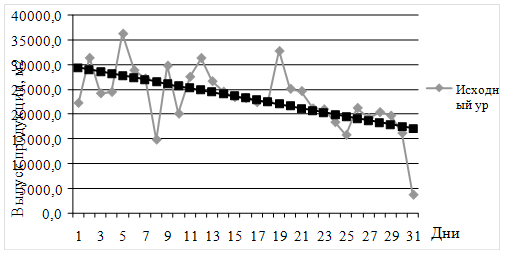Рисунок 3.2.3.3 – Графическое отображение выравнивания по прямой
Рассмотрим сглаживание по параболе второй степени. Для этого заполним таблицу 2 приложения В. На основании формул (1.2.3.5а, б) вычислим значения параметров:
; 
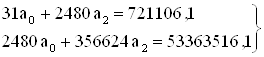
Решив систему уравнений получим а0=25448,2; а2=–27,3. В результате, используя формулу (1.2.3.4) получаем уравнение параболы, на основании которого заполняется таблица:
Отобразим полученные данные графически на рисунке 3.2.3.4.
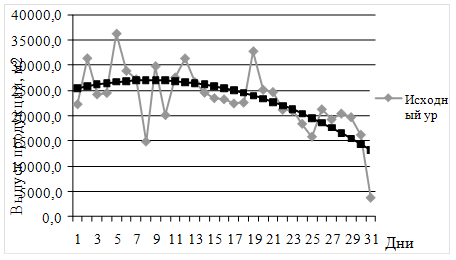Рисунок 3.2.3.4 – Графическое отображение выравнивания по параболе
Рассмотрим выравнивание с помощью логарифмической функции. Для этого заполним таблицу 3 приложения В. На основании формул (1.2.3.7а, б) вычислим значения параметров:
; 
.
Используя формулу (1.2.3.6) получаем уравнение логарифмической функции, на основании которой заполняется таблица:
Для нахождения необходимо пропотенцировать полученные значения функции. Полученные данные отобразим графически на рисунке 3.2.3.5.
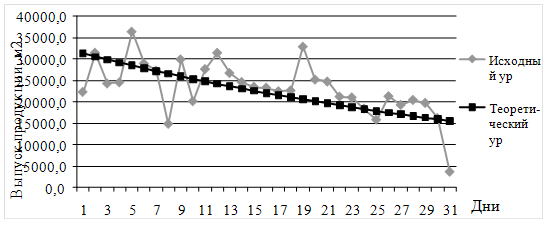
Рисунок 3.2.3.5 – Графическое отображение выравнивания с помощью логарифмической функции
Для выбора оптимальной функции из рассчитанных, воспользуемся формулой ошибки аппроксимации (1.2.3.8):
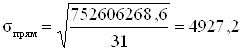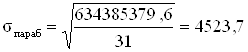м2;
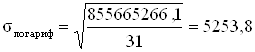м2;
м2.
Полученные значения означают отклонение фактических уровней ряда, от выравненных (расчетных). Очевидно, что самым оптимальным является выравнивание по параболе, т.к. оно имеет минимальное отклонение по сравнению с остальными функциями.
На основании проведенного аналитического выравнивания различными методами и функциями можно сделать вывод об общей динамике в производстве продукции по дням. Выравнивание 3 методами показало, что наибольший выпуск наблюдается в середине месяца и последующим спадом к концу месяца. Т.к. оптимальной является параболическая функция из-за наименьшей ошибки аппроксимации, то средний выпуск ежедневно составляет 5959,6±4523,7м2.
Похожие работы
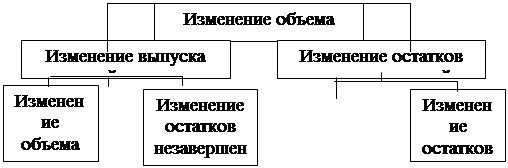
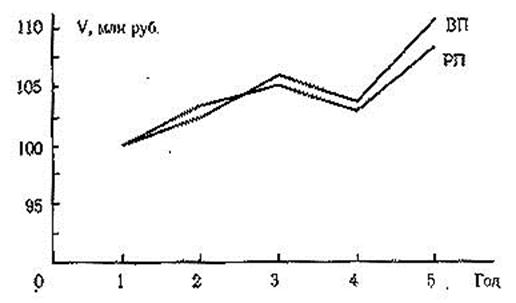
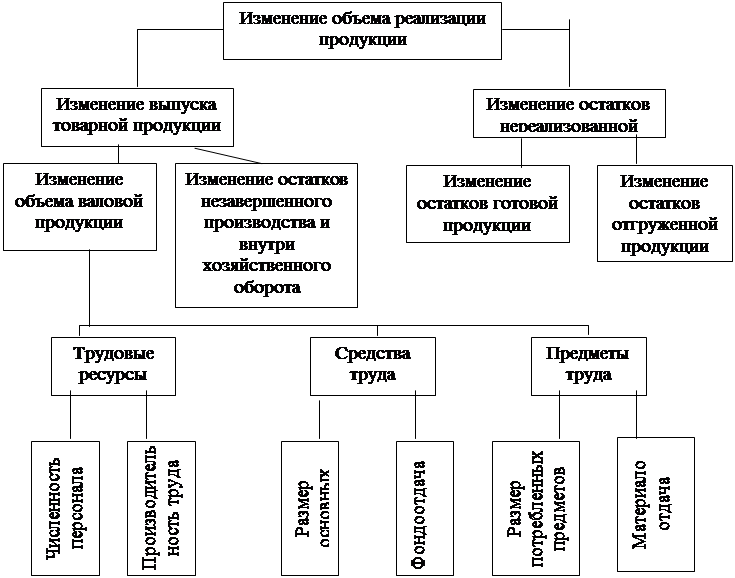
... и иных внеоборотных активов; - уплаченные штрафы и пени за нарушение налогового законодательства, осуществляемые за счет чистой прибыли предприятия; Глава II. Анализ производства и реализации продукции СПК «Скуратовский» 2.1. Технико-экономическая характеристика предприятия. Общество с ограниченной ответственностью промышленно-коммерческая фирма СПК «Скуратовский» был зарегистрирован 14 ...
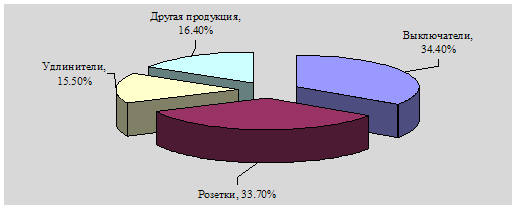
... Структура произведенной ЧУП "Светоприбор" за 8 мес. 2008 г. продукции по плану Рисунок 4. Структура произведенной ЧУП "Светоприбор" за 8 мес. 2008 г. продукции фактически При изучении деятельности предприятия важен анализ ритмичности производства и реализации продукции. Ритмичность - равномерный выпуск продукции в соответствии с графиком в объеме и ассортименте, предусмотренных планом. ...
... проведения самого анализа. 3.2 Анализ структуры и динамики расходов на реализацию товаров Проведем анализ расходов на реализацию товаров Столбцовского райпо. Расходы анализируемой организации характеризуются следующими данными (таблица 3.1) Таблица 3.1 Информация об издержках обращения розничной торговли Столбцовского райпо за 2002/2003 гг. Показатели Годы. Отклонение (+; -) Темп ...
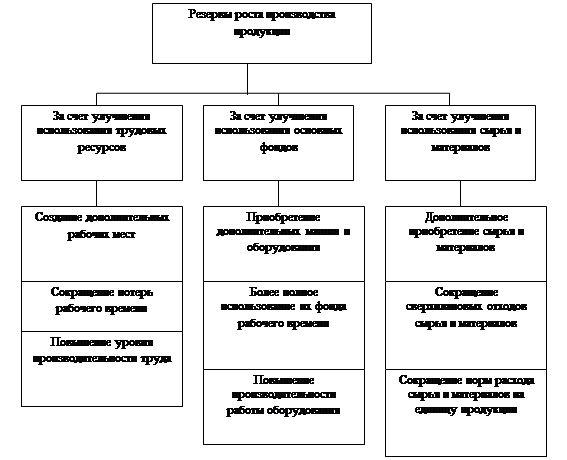
... , квалификации рабочих, аритмичность производства и др. 5 АНАЛИЗ РИТМИЧНОСТИ РАБОТЫ ПРЕДПРИЯТИЯ При изучении деятельности предприятия важен анализ ритмичности производства и реализации продукции. Ритмичность — равномерный выпуск, продукции в соответствии с графиком в объеме и ассортименте, предусмотренных планом. Ритмичная работа является основным условием своевременного выпуска и ...
0 комментариев