Навигация
Міністерство освіти і науки України
Реферат
на тему "Логіка і множини"
з дисципліни "Дискретна математика"
Харків 2011
Зміст
Вступ
1. Логічні операції над пропозиціями
2. Таблиця істинності
3. Тавтологія і логічна еквівалентність
4. Функції висловлювань і множини
5.Функції множин
6. Логіка квантифікаторів
Література
Вступ
Пропозиція це виcлів (твердження), який може бути істинним або хибним – третього не дано. В цьому полягає один із фундаментальних принципів логіки – принцип виключення третього. Істинність і хибність називаються логічними значеннями пропозиції. Пропозиція "2 + 2 = 4" істинна, а "p є раціональне число" хибна. З точки зору граматики пропозиція є речення – закінчена думка. Будемо розрізняти елементарні пропозиції і складні. Елементарній пропозиції відповідає просте речення з простими підметом і присудком. Виясняти, який з окремих елементарних висловів є істинним чи хибним, не є завданням логіки. Логіка займається знаходженням логічних значень складних пропозицій при умові, що логічні значення складових елементарних пропозицій відомі. Існує багато тверджень, істинність або хибність яких нікому не вдається довести. Наприклад, відома теорема Гольдбаха що "кожне парне число більше 2 є сумою двох простих чисел". В даному вище означенні пропозиції є великий дефект, згідно нього не завжди можна визначити, чи є дане твердження пропозицією. Наприклад, вираз "Я завжди говорю неправду". Тому інколи замість замість терміну "пропозиція" вживають більш нейтральний термін "вислів", в цьому разі не обов’язково треба знати, істинний вислів чи хибний.
1. Логічні операції над пропозиціями
Спочатку з’ясуємо правила з’єднання висловів для одержання нових висловів. Позначимо довільні вислови p і q.
Означення 1. (Кон’юнкція) Говорять, що вислів p∧q (p і q) істинний, якщо обидва вислови p, q істинні і хибний в противному випадку.
Приклад 1. Вислів "2 + 2 = 4" і "2 + 3 = 5" є істинним.
Приклад 2. Вислів "2 + 2 = 4" і "p є число раціональне" хибний.
Означення 2. (Диз’юнкція). Говорять, що вислів p ∨ q (p або q) хибний, якщо хоча б один з висловів p, q істинний, і хибний в противному випадку.
Приклад 3. Вислів "2 + 2 = 2" або "1 + 3 = 5" хибний.
Приклад 4. Вислів "2 + 2 = 4" або "p є число раціональне" істинний.
Означення 3. (Заперечення) Говоримо, що p (не p) істинний, якщо p хибний, і навпаки, хибний, якщо p iстинний.
Зауваження. В деяких підручниках замість p вживають позначення ![]() , в залежності від зручності ми будемо користуватися обома.
, в залежності від зручності ми будемо користуватися обома.
Приклад 5. Заперечення вислову "2 + 2 = 4" є вислів "2 + 2 ¹ 4".
Приклад 6. Заперечення вислову "p є число раціональне" є вислів "p є число ірраціональне". Означення 4. (Імплікація). Говорять, що вислів p → q (якщо p, то q) істинний, якщо p хибний, або q iстинний, або обидва істинні і хибний в противному випадку. Зауваження. Простіше визначити вислів p → q як хибний у випадку, коли p істинний, а q хибний. Це треба розуміти наступним чином. Якщо ми зробили хибний висновок з істинного, то наше міркування помилкове. Але допускаємо, що істинний висновок може бути одержаний і з хибного припущення.
Приклад 7. Вислів "якщо 2 + 2 = 2", то "1 + 3 = 5" істинний, тому що вислів "2 + 2 = 2" хибний.
Приклад 8. Вислів "якщо 2 + 2 = 4", то "p є число раціональне " хибний.
Приклад 9. Вислів "якщо p є число раціональне" , то "2 + 2 = 4" істинний.
Означення 5. (Еквівалентність) Говорять, що вислів p « q (p тоді і лише тоді, коли q) істинний у випадку, коли p, q істинні або хибні одночасно і хибний в противному випадку.
Приклад 10. Вислів "2 + 2 = 4" тоді і лише тоді, коли "p є число раціональне " істинний.
Приклад 11. Вислів "2 + 2 ¹ 4" тоді і лише тоді, коли "p є число раціональне " також істинний.
2. Таблиця істинності
Якщо вжити Т "true" для позначення істинного вислову і F "false" для хибного, вище наведені означення можуть бути представлені у вигляді таблиці істинності "truth table":
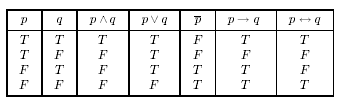
Приклад 1 Побудуємо таблицю істинності для більш складної логічної конструкції ![]()
3. Тавтологія і логічна еквівалентність
Означення 1. Тавтологія це істинний в логічному значенні вислів.
Важко привести приклад елементарної пропозиції, яку б можна було назвати тавтологією. Як правило це поняття характерне для складних пропозицій і означає, які б не були логічні значення складових пропозицій, складна пропозиція завжди буде істинною, якщо вона є тавтологією. Всі можливі комбінації логічних значень складових називаються інтерпретаціями. Вище наведені таблиці істинності показують, що для двох складових існує всього 4 інтерпретації. Якщо трохи подумати, то прийдемо до висновку, що три складові мають 23 = 8 інтерпретацій і взагалі, n складових мають 2n інтерпретацій. Використовуючи цей термін можна перефразувати означення 1.1 як : тавтологія – це пропозиція істинна при всіх інтерпретаціях її складових. Керуючись цим означенням легко довести істинність наступних пропозицій:
Приклад 1. Вислови
![]()
![]()
є тавтології. Це дає можливість писати p ∧ q ∧ r без дужок, узагальнивши поняття кон’юнкції для більше ніж двох висловів.
Приклад 2. Вислови
![]()
![]()
є тавтології. Це дає можливість писати p Ú q Ú r без дужок, узагальнивши поняття диз’юнкції для більше ніж двох висловів.
Приклад 3. Вислів p ∨ p є тавтологія.
Приклад 4. Вислів (p → q) « (q → p) є тавтологія.
Приклад 5. Вислів (p → q) « (p ∨ q) є тавтологія.
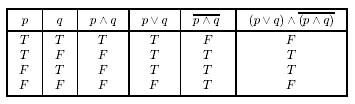
Приклад 6. Вислів (p « q) « ((p∨q)∧(p ∧ q)) є тавтологія; про що свідчить наступна таблиця істинності:

Пропонуємо студентам довести, що наступні вислови є тавтології.
Розподільний закон.
(a) (p ∧ (q ∨ r)) « ((p ∧ q) ∨ (p ∧ r)); (b) (p ∨ (q ∧ r)) « ((p ∨ q) ∧ (p ∨ r)).
Закон де Моргана.
(a) (p ∧ q) « (p ∨ q); (b) (p ∨ q) « (p ∧ q).
Правила виводу.
(a) (MODUS PONENS) (p ∧ (p → q)) → q;
(b) (MODUS TOLLENS) ((p → q) ∧ q) → p;
(c) (SYLLOGISM) ((p → q) ∧ (q → r)) → (p → r).
Всі ці закони з точки зору логіки є тавтології, що можна легко довести за допомогою таблиці істинності.
Означення 1. Говорять, що вислови p і q логічно еквівалентні, якщо вислів p « q є тавтологія.
Приклад 7. Вислови p → q і q → p логічно еквівалентні. Останній вислів називають контра позицією першого.
Зауваження. Вислови p → q і q → p не є логічно еквівалентними. Останній називається обернений до першого.
Похожие работы
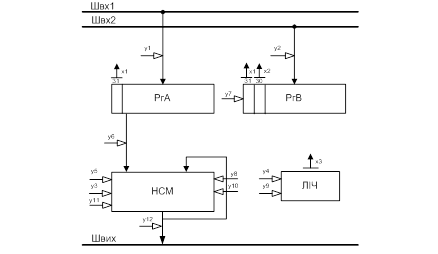
... льш прості операції які називаються мікроопераціями тобто кожна операція – це визначена послідовність мікрооперацій. Існують два основні типи керуючих автоматів 1. Керуючий автомат з жорсткою чи схемною логікою. Для кожної операції будується набір комбінаційних схем які в потрібних тактах збуджують відповідні керуючі сигнали. Іншими словами ...
... людей. А заперечне судження, в якому суб'єкт і предикат проголошуються несумісними поняттями «Українці не нація», теж не відповідає дійсності. Формальна логіка абстрагується від діалектики абсолютного і відносного в істині. Вона виходить з абсолютного протиставлення істинних і хибних суджень, розглядаючи кожне з них або як істинне і тільки істинне, або як хибне і тільки хибне (тризначна логіка, ...
... з двох способів уживання слова "або" в українській мові. Диз'юнкція істинна, якщо істинне принаймні одне з двох висловлювань. Наприклад, її використовують у реченні "Лекції з логіки можуть відвідувати студенти, які прослухали курси математичного аналізу або дискретної математики". Зміст цього речення полягає в тому, що лекції можуть відвідувати як студенти, які прослухали обидва курси, так і ті ...
... завжди істинною, а відповідно, й не є логічним законом. Можна сказати, що неможливість подати закон достатньої підстави у вигляді формули була своєрідним свідченням того, що основні формально-логічні закони (або закони логіки) мають зовсім іншу природу, ніж завжди істинні формули, і виконують своєрідну функцію у процесі побудови та аналізу наших міркувань. Запис законів логіки у вигляді формул і ...
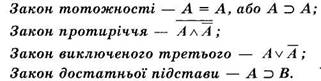
0 комментариев