Навигация
Функції висловлювань і множини
4. Функції висловлювань і множини
В багатьох випадках ми вживаємо вислови типу "x є парне число", що містять одну або декілька змінних. Ми будемо називати їх функціями висловлювань або пропозицій. В наведеному прикладі вислів є істинний для одних значень х і хибний для інших. Виникають наступні питання:
Які значення x допустимі?
Чи вислів є істинним при всіх допустимих значеннях x ?
При яких саме допустимих значеннях x вислів є істинним?
Щоб відповісти на ці питання нам потрібно поняття множини. Нехай Р є множина і х є елемент цієї множини. Цей факт позначають x ∈ P. Елементи множини можна задати двома способами:
· Перечисленням, наприклад {1, 2, 3} означає множину, що складається з чисел 1, 2, 3 і нічого більше;
· Визначенням властивості (функції висловлювань p(x)). В цьому випадку важливо визначити множину U допустимих значень x . Тоді можемо написати
P = {x : x ∈ U і p(x) істинно} або, просто , P = {x : p(x)}.
Множина без жодного елемента називається пустою і позначається Æ.
N = {1, 2, 3, 4, 5, ...} називається множиною натуральних чисел.
Z = {. . . ,-2,-1, 0, 1, 2, . . .} називається множиною цілих чисел.
{x : x ∈ N і -2 < x < 2} = {1}.
{x : x ∈ Z і -2 < x < 2} = {-1, 0, 1}.
{x : x ∈ N і -1 < x < 1} = Æ.
5. Функції множин
Припустимо, що функції висловів p(x), q(x) відносяться до множин P, Q, тобто P = {x : p(x)} і Q = {x : q(x)}. Визначимо наступні операції над множинами перетин P ∩ Q = {x : p(x) ∧ q(x)};
об’єднання P ∪ Q = {x : p(x) ∨ q(x)};
доповнення CP = {x : p(x)};
різницю P \ Q = {x : p(x) ∧ q(x)}.
Ці означення легко перефразувати у форму
P ∩ Q = {x : x ∈ P і x ∈ Q};
P ∪ Q = {x : x ∈ P або x ∈ Q};
СP = {x : x Ï P};
P \ Q = {x : x ∈ P і x Ï Q}.
Множина P є підмножиною Q і позначається P ⊆ Q або Q ⊇ P, якщо кожен елемент P є елементом Q. Іншими словами, для множин P = {x : p(x)} і Q = {x : q(x)} маємо P ⊆ Q тоді і тільки тоді, коли p(x) → q(x) для всіх допустимих значень x ∈ U.
Множини P і Q називаються рівними P = Q якщо вони містять ті ж самі елементи, іншими словами, якщо P ⊆ Q і Q ⊆ P.
Множина P називається власною підмножиною Q і позначається P ⊂ Q або Q ⊃ P, якщо P ⊆ Q і P ¹ Q.
Наступні властивості функцій множин можуть бути легко доведені на основі їх аналогів в логіці.
Розподільний закон. Якщо P,Q,R є множини, то
(a) P ∩ (Q ∪ R) = (P ∩ Q) ∪ (P ∩ R);
(b) P ∪ (Q ∩ R) = (P ∪ Q) ∩ (P ∪ R).
логіка тавтологія еквівалентність квантифікатор
Закон де Моргана. Якщо P,Q є множини, то
(a) С (P ∩ Q) = СP∪ СQ;
(b) С(P ∪ Q) = СP ∩ СQ.
Зробимо це, наприклад, для першого розподільного закону. Припустимо, що функції p(x), q(x), r(x) відносяться до множин P, Q, R , тобто P = {x : p(x)}, Q = {x : q(x)} і R = {x : r(x)}. Тоді
P ∩ (Q ∪ R) = {x : p(x) ∧ (q(x) ∨ r(x))}
(P ∩ Q) ∪ (P ∩ R) = {x : (p(x) ∧ q(x)) ∨ (p(x) ∧ r(x))}.
Припустимо, що x ∈ P ∩ (Q ∪ R). Тоді p(x) ∧ (q(x) ∨ r(x)) істинно. По першому розподільному закону для логічних функцій маємо тавтологію
(p(x) ∧ (q(x) ∨ r(x))) « ((p(x) ∧ q(x)) ∨ (p(x) ∧ r(x)))
Звідси слідує, що (p(x) ∧ q(x)) ∨ (p(x) ∧ r(x)) істинно, так що x ∈ (P ∩ Q) ∪ (P ∩ R). А це значить, що
(1) P ∩ (Q ∪ R) ⊆ (P ∩ Q) ∪ (P ∩ R).
Тепер припустимо, що x ∈ (P ∩ Q) ∪ (P ∩ R). Тоді (p(x) ∧ q(x)) ∨ (p(x) ∧ r(x)) істинно. З першого розподільного закону для логічних функцій слідує, що p(x) ∧ (q(x) ∨ r(x)) істинно, так що x ∈ P ∩ (Q ∪ R). Це дає
(2) (P ∩ Q) ∪ (P ∩ R) ⊆ P ∩ (Q ∪ R).
Потрібний результат слідує з (1) і (2).
6. Логіка квантифікаторів
Повернемось до прикладу "x є парне число". Обмежимо x множиною цілих чисел Z . Tоді вислів "x є парне число" істинний лише для деяких x в Z. Звідси слідує, що вислів "деякі x ∈ Z парні" істинний, якщо вислів "всі x ∈ Z непарні" хибний.
В загальному випадку розглянемо функцію вислів p(x) в якій змінна x належить певній множині. Введемо наступні позначення для висловів
∀x, p(x) (для всіх x, p(x) істинний);
і
∃x, p(x) (для деяких x, p(x) істинний).
Символ ∀ (для всіх) і ∃ (для деяких) називаються відповідно універсальним квантифікатором і квантифікатором існування. Зауважимо, що змінна x не є суттєва, вона може бути замінена будь якою іншою, так що ∀x, p(x) і ∀y, p(y) означають одне й те ж саме.
(Теорема Лагранжа) Кожне натуральне число є сума квадратів чотирьох цілих чисел. Це можна записати як
∀n ∈ N, ∃a, b, c, d ∈ Z, n = a2 + b2 + c2 + d2.
(Гіпотеза Гольдбаха) Кожне парне число більше 2 є сума двох простих чисел. Це можна записати як
∀n ∈ N \ {1}, ∃p, q прості, 2n = p + q.
Ще невідомо, чи це дійсно так. Це одна з найцікавіших з ще не розв’язаних проблем математики.
Заперечення
Розглянемо заперечення висловів з квантифікаторами. Давайте скажемо, що всі люди дурні. Дехто з вас з цим не погодиться. Можна здогадатися, що запереченням вислову ∀x, p(x) буде вислів ∃x, p(x). Тепер будемо не так категоричними і скажемо, що дехто з вас дурень. Якщо і цього разу заперечите, то запереченням вислову ∃x, p(x) буде ∀x, p(x). Отже, маємо формули аналогічні законам де Моргана для квантіфікаторів
∀x, p(x) « ∃x, p(x)
∃x, p(x) « ∀x, p(x).
Підсумовуючи сказане, заперечуючи вислів з кавантифікатрором ми змінюємо квантифікатор і заперечуємо функцію висловів. Застосовуючи це правило послідовно декілька раз одержимо заперечення більш складного вислову
![]()
спочатку як
![]()
Потім
![]()
Потім
![]()
і, нарешті,
![]()
Запереченням гіпотези Гольдбаха в термінах квантифікаторів буде
∃n ∈ N \ {1}, ∀p, q прості числа, 2n ¹ p + q.
Іншими словами, існує парне число більше 2, яке не є сумою двох простих чисел. Отже, щоб відкинути гіпотезу Гольдбаха досить знайти таке число. Це називається "привести контр приклад".
Література
1. Вища математика: Основні означення, приклади і задачі. У 2-х кн. / За ред. І.П.Васильченко. _ К: Либідь, 1994.- 280 ст.
2. Шкіль М.І. Вища математика: Підручник у 3-х кн./ Шкіль М.І., Колеснік Т.В., Котлова В.М. – К.: Либідь, 1994.
3. Вища математика: Основні означення, приклади і задачі. У 2-х кн. / За ред. Г.Л. Кулініча: Підручник К.: Либідь, 1994.
4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. - М.: Наука, 1985.
5. Карасев А.И., Аксютина Э.М., Савельева Т.И. Курс высшей математики для экономических вузов. М.: Высшая школа. ч. 1,2. 1990.
6. Пискунов Н.С. Дифференциальное и интегральное исчисление. - М.: Наука, 1988, т.1,2.
7. Ильин В.Н., Позняк З.Г. Аналитическая геометрия. М. :Наука, 1984.
8. Ильин В.Н., Позняк З.Г. Линейная алгебра. М.: Наука, 1989.
9. Бахвалов С.В. Аналитическая геометрия. - М.: Высшая школа, 1992.
10. Цубербиллер О.Н. Задачи по аналитической геометрии. М.: Высшая школа, 1984.
Похожие работы
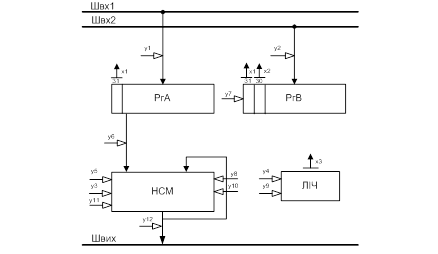
... льш прості операції які називаються мікроопераціями тобто кожна операція – це визначена послідовність мікрооперацій. Існують два основні типи керуючих автоматів 1. Керуючий автомат з жорсткою чи схемною логікою. Для кожної операції будується набір комбінаційних схем які в потрібних тактах збуджують відповідні керуючі сигнали. Іншими словами ...
... людей. А заперечне судження, в якому суб'єкт і предикат проголошуються несумісними поняттями «Українці не нація», теж не відповідає дійсності. Формальна логіка абстрагується від діалектики абсолютного і відносного в істині. Вона виходить з абсолютного протиставлення істинних і хибних суджень, розглядаючи кожне з них або як істинне і тільки істинне, або як хибне і тільки хибне (тризначна логіка, ...
... з двох способів уживання слова "або" в українській мові. Диз'юнкція істинна, якщо істинне принаймні одне з двох висловлювань. Наприклад, її використовують у реченні "Лекції з логіки можуть відвідувати студенти, які прослухали курси математичного аналізу або дискретної математики". Зміст цього речення полягає в тому, що лекції можуть відвідувати як студенти, які прослухали обидва курси, так і ті ...
... завжди істинною, а відповідно, й не є логічним законом. Можна сказати, що неможливість подати закон достатньої підстави у вигляді формули була своєрідним свідченням того, що основні формально-логічні закони (або закони логіки) мають зовсім іншу природу, ніж завжди істинні формули, і виконують своєрідну функцію у процесі побудови та аналізу наших міркувань. Запис законів логіки у вигляді формул і ...
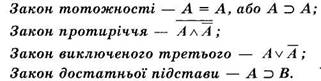
0 комментариев