Генеральный подрядчик организовывает и отвечает за строительство в целом, за качество выполняемых работ, за соблюдение срока работ;
Определение тенденций динамики ввода в действие жилья и среднемесячной заработной платы
Индексный факторный анализ производительности труда
Характеристика и экономический анализ показателей
Построение корреляционных уравнений
Оценка силы корреляции
Навигация
Построение корреляционных уравнений
Статистическая оценка деятельности предприятия строительной отрасли
49421
знак
27
таблиц
15
изображений
2.3 Построение корреляционных уравнений
Уравнение параболы имеет вид:
(2.2)
Применяя метод наименьших квадратов, получим разрешающую систему уравнений:
Нахождение параметров уравнения парной корреляции для связи между Х и Y для уравнения прямой
| № | x | y | xy | x^2 | y(x) | y-y(x) | (y-y(x))^2 |
| 1 | 3090,6 | 5093,3 | 15741353 | 9551808,4 | 5069,46 | 23,8423 | 568,454 |
| 2 | 5189,2 | 5138,1 | 26662629 | 26927797 | 5101,75 | 36,3487 | 1321,23 |
| 3 | 5841,5 | 5063,1 | 29575982 | 34123122 | 5111,79 | -48,689 | 2370,62 |
| 4 | 5958,2 | 4969,3 | 29608083 | 35500147 | 5113,58 | -144,28 | 20818,1 |
| 5 | 6640,7 | 5256,9 | 34909429 | 44098896 | 5124,09 | 132,813 | 17639,2 |
| Итог | 26720,2 | 25520,67 | 136497476 | 150201770 | 25520,7 | 0 | 42717,6 |
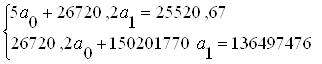
Решив систему матричным методом, находим:
= 5021,8991
= 0,01538815
Отсюда, уравнение прямой имеет вид: yx = 5018,47+0,02 x
Таблица 2.5. Нахождение параметров уравнения парной корреляции для связи между X и Y по параболе
| № | x | y | x*y | x^2 | x2*y | x^3 | x^4 | y(x) |
| 1 | 3090,6 | 5093,3 | 15741353 | 9551808,4 | 48650225724 | 29520818917 | 91237042946166 | 4728,821611 |
| 2 | 5189,2 | 5138,1 | 26662629 | 26927797 | 138355020986 | 13971756626 | 725106231885195 | 3978,723378 |
| 3 | 5841,5 | 5063,1 | 29575982 | 34123122 | 172765366686 | 199279038321 | 1164387472088440 | 3745,573146 |
| 4 | 5958,2 | 4969,3 | 29608083 | 35500147 | 211516975855,4 | 211495677912 | 1260260454061680 | 3703,861308 |
| 5 | 6640,7 | 5256,9 | 34909429 | 44098896 | 23182789672 | 292754944000 | 194471267135730 | 3459,916752 |
| Σ | 26720,2 | 25520,67 | 136497476 | 150201770 | 754465259799,4 | 843247226502 | 5185703872617220 | 25520,67 |
| Y-Y(x) | (Y-Y(x))^2 |
| 364,4783888 | 132844,4959 |
| 1159,376622 | 1344154,151 |
| -1317,526854 | 1735877,011 |
| 1265,438692 | 1601335,084 |
| -1796,983248 | 3229148,792 |
| 0 | 8043359,534 |
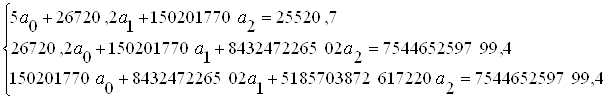
Решив систему методом обратной матрицы, находим:
= 5833,488341, =-0,357426816 
=0
Следовательно, уравнение параболы имеет вид:
Чтобы узнать, какое из уравнений – параболы или прямой – лучше описывает корреляционную связь, рассчитаем среднюю квадратическую ошибку:
Для прямой: 
а также коэффициент вариации: 
Для параболы:
и 
Так как коэффициент вариации для уравнения прямой меньше, чем для уравнения параболы, уравнение прямой более точно описывает корреляционную связь между поизводительностью труда 1 работника и рентабельности.
Таблица 2.6. Нахождение параметров уравнения парной корреляции для связи между V и Y для уравнения прямой
| № | v | y | v^2 | v*y | y(v) | y-y(v) | (y-y(v))^2 |
| 1 | 11857 | 5093,3 | 140586552 | 60390850,6 | 5218,623 | -125,3232 | 15705,90446 |
| 2 | 13172 | 5256,9 | 173499476 | 69243334,5 | 5166,023 | 90,8668 | 8256,775342 |
| 3 | 13218 | 5138,1 | 174709444 | 67914224 | 5164,189 | -26,0892 | 680,6463566 |
| 4 | 14569 | 5063,1 | 212262754 | 73765227,7 | 5110,13 | -47,0504 | 2213,74014 |
| 5 | 14775 | 4969,3 | 218286441 | 73419022,2 | 5101,919 | -132,6192 | 17587,85221 |
| Итого | 67590,37 | 25520,67 | 919344668 | 344732659 | 25520,67 | 0 | 44444,9 |
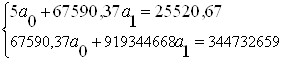
Решив систему матричным методом, находим:
= 5692.89
= -0.04
Отсюда, уравнение прямой имеет вид:
Таблица 2.7. Нахождение параметров уравнения парной корреляции для связи между V и Y по параболе
| № | v | y | v*y | v^2 | v^2y | v^3 | v^4 | y(v) |
| ||
| 1 | 11857 | 5093,3 | 60390850,6 | 140586552 | 716049485302 | 1666957239793 | 19765111992225600 | 5188,935877 | |||
| 2 | 13172 | 5256,9 | 69243334,5 | 173499476 | 912069395384 | 2285362864448 | 30102799650509100 | 5122,197135 | |||
| 3 | 13218 | 5138,1 | 67914224 | 174709444 | 897674594216 | 2309389796232 | 30525514326594600 | 5119,862547 | |||
| 4 | 14569 | 5063,1 | 73765227,7 | 212262754 | 1074707549777 | 3092354182009 | 45052508077689100 | 5051,296737 | |||
| 5 | 14775 | 4969,3 | 73419022,2 | 218286441 | 1084730811261 | 3225391734375 | 47655162875390600 | 5040,841846 | |||
| Итог | 67590,37 | 25520,67 | 344732659 | 919344668 | 4685231835941 | 12579455816857 | 173101096922409000 | 25520,67 | |||
| y-y(v) | (y-y(v))^2 |
| |||||||||
| -95,6358768 | 9146,220948 |
| |||||||||
| 134,7028654 | 18144,86194 |
| |||||||||
| 18,23745257 | 332,6046763 |
| |||||||||
| 11,80326308 | 139,3170193 |
| |||||||||
| -71,5418465 | 5118,2358 |
| |||||||||
| 0 | 32881,24039 |
| |||||||||
Решив систему методом обратной матрицы, находим:
=5790,701099 a1= -0,050751895 , 
a2= 0
Следовательно, уравнение параболы имеет вид:
Чтобы узнать, какое из уравнений – прямой или параболы – лучше описывает корреляционную связь, рассчитаем:
Для прямой:
а также коэффициент вариации:
Для параболы:
и 
Так как коэффициент вариации для уравнения прямой меньше, чем для уравнения параболы, уравнение прямой более точно описывает корреляционную связь между выручкой и рентабельностью.
Таблица 2.8. Нахождение параметров уравнения парной корреляции для связи между X и V по прямой
| № | x | v | x*v | x^2 | v(x) | v-v(x) | (v-v(x))^2 |
| 1 | 3090,6 | 11856,92 | 36644996,95 | 9551808,36 | 12107,98058 | -251,0605779 | 63031,4138 |
| 2 | 5189,2 | 13217,77 | 68589652,08 | 26927796,64 | 13421,18264 | -203,4126404 | 41376,70226 |
| 3 | 5841,5 | 14569,24 | 85106215,46 | 34123122,25 | 13829,36033 | 739,8796672 | 547421,922 |
| 4 | 5958,2 | 14774,52 | 88029545,06 | 35500147,24 | 13902,38553 | 872,1344691 | 760618,5323 |
| 5 | 6640,7 | 13171,92 | 87470769,14 | 44098896,49 | 14329,46092 | -1157,540918 | 1339900,977 |
| Итог | 26720,2 | 67590,4 | 365841179 | 150201771 | 67590,37 | 0,00 | 2752349,547 |
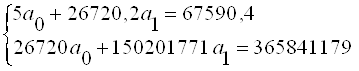
Решив систему методом обратной матрицы, находим:
= 10174,03; =0,625751
Следовательно, уравнение прямой имеет вид:
Таблица 2.9. Нахождение параметров уравнения парной корреляции для связи между Х и V по параболе
| № | x | v | x*v | x^2 | x^2v | x^3 | x^4 | v(x) |
| 1 | 3090,6 | 11856,92 | 36644996,95 | 9551808,36 | 113255027579,9 | 29520818917,4 | 91237042946165,9 | 11688,07134 |
| 2 | 5189,2 | 13217,77 | 68589652,08 | 26927796,64 | 355925422594,3 | 139733722324,3 | 725106231885195,0 | 14080,87648 |
| 3 | 5841,5 | 14569,24 | 85106215,46 | 34123122,25 | 497147957609,6 | 199330218623,4 | 1164387472088440,0 | 14113,05705 |
| 4 | 5958,2 | 14774,52 | 88029545,06 | 35500147,24 | 524497635400,3 | 211516977285,4 | 1260260454061680,0 | 14084,71225 |
| 5 | 6640,7 | 13171,92 | 87470769,14 | 44098896,49 | 580867136654,6 | 292847541921,1 | 1944712671635730,0 | 13711,67003 |
| Σ | 26720,2 | 67590,4 | 365841179 | 150201771 | 2071693179838,6 | 872949279071,6 | 5185703872617220,0 | 67590,38714 |
| v-v(x) | (v-v(x))^2 |
| ||||||
| 168,84866 | 28509,87 |
| ||||||
| -863,10648 | 744952,79 |
| ||||||
| 456,18296 | 208102,89 |
| ||||||
| 689,80775 | 475834,73 |
| ||||||
| -539,75003 | 291330,1 |
| ||||||
| 0 | 1748730,4 |
| ||||||
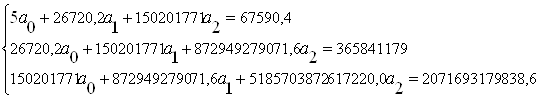
Решив систему методом обратной матрицы, находим:
= 2306,042255; = 4,24, = -0,00038.
Следовательно, уравнение прямой имеет вид:
Среднее значение выручки за вычетом НДС: 
.
Чтобы узнать, какое из уравнений – прямой или параболы – лучше описывает корреляционную связь между производительностью труда 1 работника и рентабельностью, рассчитаем:
Для прямой: 
а также коэффициент вариации: 
Для параболы: 
и 
Так как коэффициент вариации для уравнения параболы меньше, чем для уравнения прямой, уравнение параболы более точно описывает корреляционную связь.
Похожие работы
... на балансе предприятия, так как в отчетном периоде возросло число служебных командировок (отсюда перерасход по статье командировочных расходов). 4. Эколого-экономические предложения по деятельности предприятия МУП «Теплотехнология» 4.1 Разработка программы по энергосбережению Основа реформирования ЖКХ заключается в комплексе мер, направленных на снижение издержек при производстве услуг ...
... ). 2. Бородкин К. В. «Комплексные методы финансовой диагностики». – Воронеж: Воронежский Государственный Университет. – 2002. – 183 с. 3. Грищенко О. В. Анализ и диагностика финансово-хозяйственной деятельности предприятия: Учебное пособие. Таганрог: Изд-во ТРТУ, 200. 112 с. 4. Ковалёв А. И., Привалов В. П. «Анализ финансового состояния предприятия». – Издание 2-е, ...
... том, что рассматриваемое в данном проекте предприятие ООО «ЛесКо» имеет реальную возможность занять определенную нишу на данном рынке, при имеющейся достаточной для производства сырьевой базе. 3. анализ инвестиционной деятельности предприятия ООО «ЛесКо» 3.1 Организационно-экономическая характеристика предприятия ООО «ЛесКо» Общество с ограниченной ответственностью «ЛесКо» создано в 2001 ...
... , рентабельность падает, что является аргументом в пользу сбалансированного штата сотрудников. [18] Выводы В результате проведённого исследования по теме: «Прибыль и рентабельность как основные показатели производственно-хозяйственной и коммерческой деятельности предприятия» можно сделать ряд выводов: На протяжении последних двух лет (2003-2004 гг.) рентабельность произведенной продукции в ...
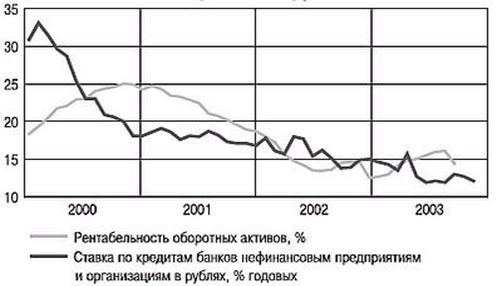
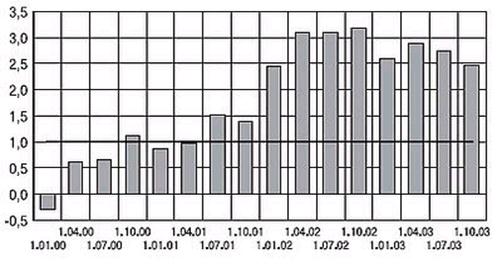
0 комментариев