Комплексна випадкова величина, характеристичні функції

2. Комплексна випадкова величина, характеристичні функції

Комплексна випадкова величина, що вводиться за формулою , є іншим способом опису випадкового вектора (,).

Випадкові величини  і  називаються незалежними, якщо незалежними є випадкові вектори (,) і (,).

,

,

,

,

,

,

,

,

.

Характеристичною функцією випадкової величини  називається середнє значення виразу .

.

Функцію  називають також характеристичною функцією відповідного закону розподілу:

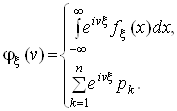 (2)

Як видно з (2), характеристична функція  є перетворенням Фур'є відповідної їй щільності імовірності:

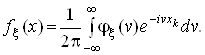
Властивість 1. При додаванні незалежних випадкових величин їхні характеристичні функції перемножуються.

Властивість 2. Розкладання характеристичної функції в ряд за ступенями  дозволяє знайти всі моменти , , ,…випадкової величини .

3. Види збіжності випадкових величин

Послідовність випадкових величин x₁, x₂…називається такою, що збігається з випадковою величиною x в розумінні середнього квадратичного, якщо границя математичного сподівання квадрата абсолютного значення відхилення  від  прямує до нуля за умови, що , тобто

.

Величина x називається ще СК границею послідовності {x_n}.

 чи .

Оскільки

,

СК збіжність рівносильна виконанню умов:

.

Послідовність випадкових величин  збігається з випадковою величиною  при  за імовірністю, якщо для кожного будь-якого e>0

,

.

Збіжність послідовності  до випадкової величини  за ймовірністю символічно позначається таким чином:

.

Для будь-якої випадкової величини  при будь-якому e>0

.

.

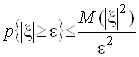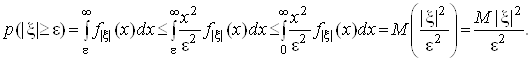
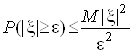Наслідок.

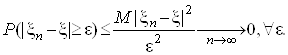
Зі збіжності у СК випливає збіжність за ймовірністю.

4. Граничні теореми теорії ймовірностей

Нерівність Чебишева.

.

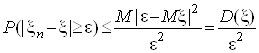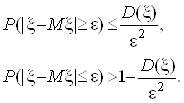(3)

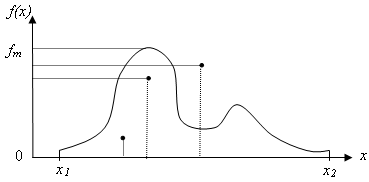
Як випливає з нерівностей (3) зі зменшенням дисперсії , основна частина площі під кривої f_x(x) виявляється зосередженою в околі точки .

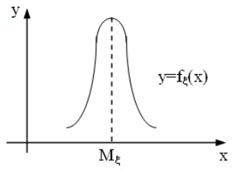
Рисунок 1

Внаслідок своєї загальності нерівність Чебишева дає дуже грубу оцінку ймовірності, що входить до неї.

Наприклад, .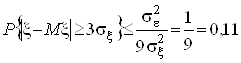

, якщо .

Вважають, що послідовність функцій розподілу , , ,...., ,... збігається до функції розподілу , якщо

в усіх точках неперервності.

Якщо , то .

Практичне використання теорії ймовірностей засновано на такому принципі: випадкову подію, ймовірність якої досить близька до 1, можна вважати достовірною та неможливою при дуже малій ймовірності.

Теореми, що забезпечують виконання такої схеми обробки даних, називаються законами великих чисел.

Теорема Чебишева

Нехай h₁, h₂…–послідовність попарно незалежних випадкових величин, дисперсії яких обмежені

, k=1,2 …

Тоді при будь-якому e>0

.

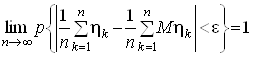Теорема Бернуллі.

Нехай x_n – число появ деякої події А в серії з n незалежних іспитів, р – ймовірність появи А в окремому іспиті.

Тоді

тобто для кожного e>0

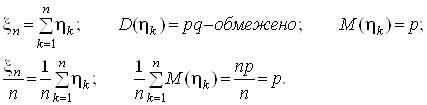
Застосовуючи теорему Чебишева, одержимо формулу, що очікуємо при необмеженій кількості випробувань.

®р.

Збіг теоретичних розрахунків із закономірностями, що фактично спостерігаються, свідчить про правильну схему побудови теорії ймовірностей. збіжність випадковий величина ймовірність

Центральна гранична теорема.

Нехай x₁,x₂,…послідовність незалежних випадкових величин, що мають дисперсію D₁,D₂,…D_n…Треті абсолютні центральні моменти їх обмежені m_k=M|x_k-Mx_k|³£C.

Тоді випадкова величина

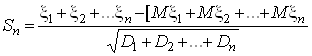
розподілена асимптотично нормально із середнім  і , тобто

Р(a<S_n<b)®Ф(b)-Ф(a)

при n®¥.

Теорема Муавра-Лапласса (окремий випадок).

Нехай x_n – число появ деякої події А у серії з n незалежних випробувань, р – ймовірність появи події А в окремому випробуванні. Тоді

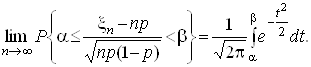
Теорема дозволяє при досить великих n одержати ймовірність:

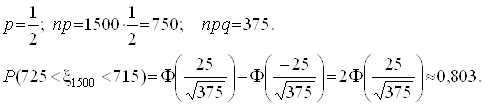
Приклад 1. Обчислити ймовірність Р(715<x_n<725) того, що кількість появ герба в 1500 киданнях буде в межах від 715 до 725.